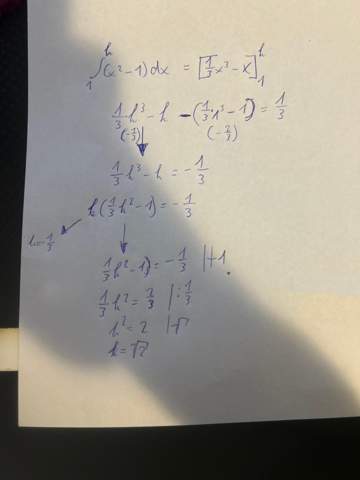Analysis – die neusten Beiträge

Guten Mittag,

ich habe ein paar Fragen zu dem Aufgabenteil b) und freue mich über eure hilfreichen Antworten sehr. :-)

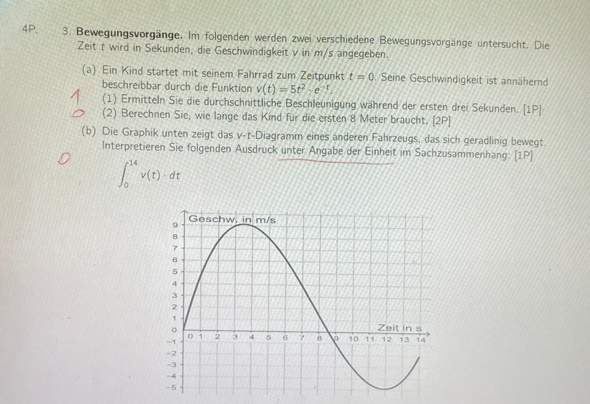
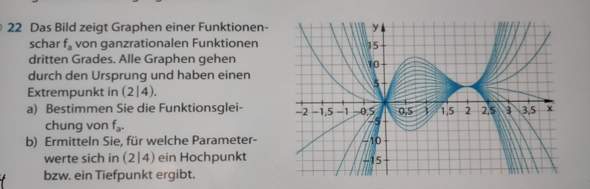
1. Um bei Aufgabenteil b) alle Punkte mit waagerechter Tangente zu erhalten, habe ich f‘(x) = 0 gesetzt. Nun habe ich jedoch einmal (x-1)^(2) und daraus erhalte ich x1/2 = 1, ist das richtig?
2. Schreibt man in diesem Fall bei b), obwohl das Ergebnis ja nicht +-1 ist (da ja keine Wurzel gezogen wurde) wirklich auch x1/2 = 1 und nicht x1 = 1?
3. Hat man in diesem Fall, dass man eine doppelte Nullstelle der 1. Ableitung als Ergebnis erhält, immer einen Sattelpunkt (wie hier bei b))?
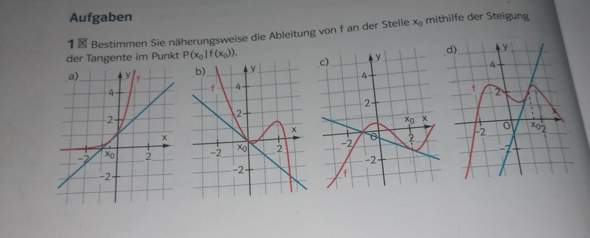
4. Muss ich bei dem Aufgabenteil a) auch folgendes schreiben: x1 = -1; x2/3/4 = 1? Denn dort handelt es sich ja einmal um eine einfache Nullstelle und einmal um eine dreifache Nullstelle. Natürlich würde ich das niemals so schreiben, aber das muss ich hier ja nun auch fragen, da meine Unsicherheit bei b) sich ja auch auf etwas Ähnliches bezieht.

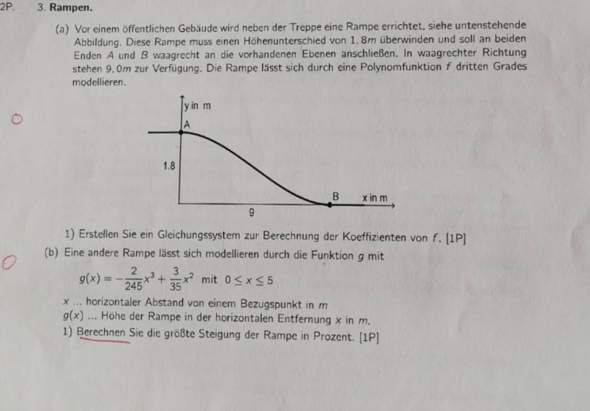
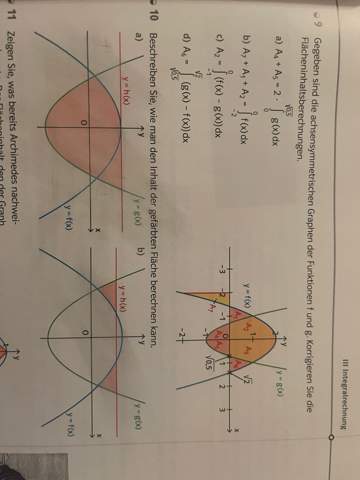
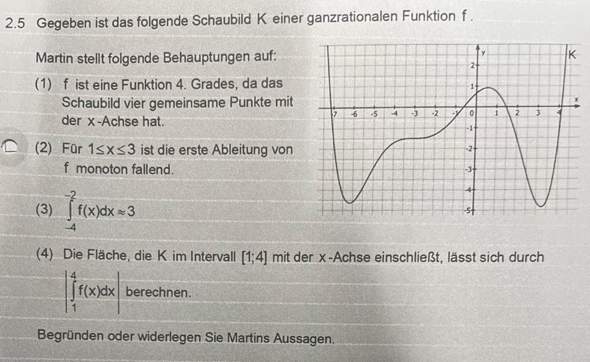
[Aufgabenstellung]

[Aufgabenteil a)]

[Aufgabenteil b)]

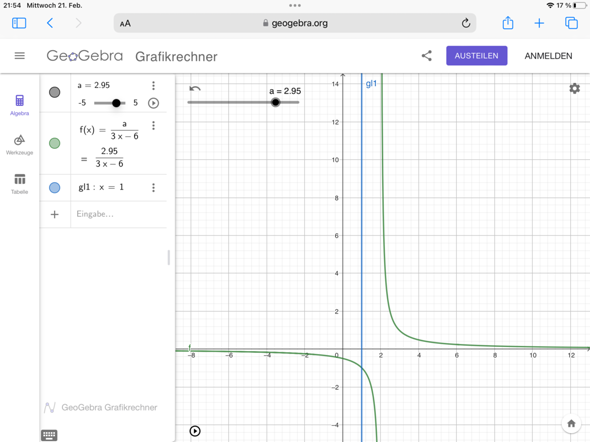
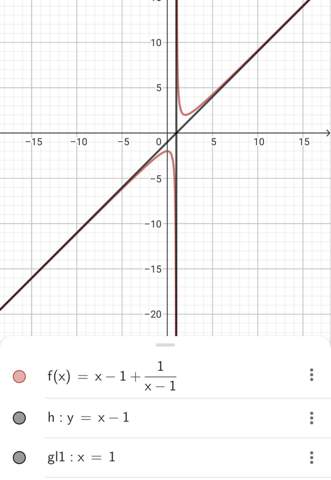
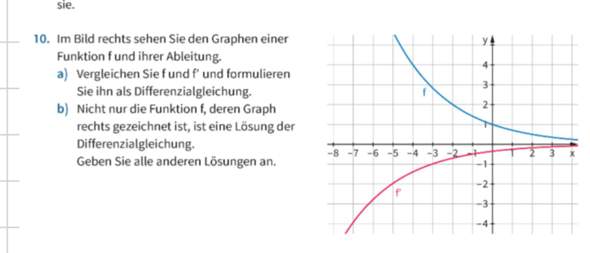
[Geogebra: Schaubild der Funktion f (in blau) und Schaubild der Funktion f‘ (in grün)]

Hallo,

ich habe diese Trigonometrie-Aufgabe berechnet und mein Ergebnis weicht komplett von der Lösung ab. Ich weiß aber wirklich nicht, warum….

Und ich verstehe auch die Auflösung der Gleichung in der Lösungsskzizze nicht. Warum steht in der zweiten Zeile der Gleichung plötzlich (tan(18)-tan(11)) und was ist mit dem (x +100) in der ersten Zeile der Gleichung passiert?

Danke für Hilfe!

bei mir kommt bei fast allen koeffizienten 0 raus

ich hätte gesagt m ist direkt proportional zu a)

Oder spielt die Proportionalität bei a) keine Rolle?

bei b) hab ich keine Ahnung

Hallo,

ich verstehe nicht so ganz was die x jetzt sein soll. Ist das dann einfach die 1

wenn man das in den Taschen Rechner eingibt also dann: 1 geteilt durch ein viertel oder wie gibt man das in den Taschenrechner

und was ist die Lösung ?

Wie kann ich mir bzgl. einer reellen Potenzreihe den Konvergenzradius vorstellen?
Dass der Konvergenzradius eine "Scheibe" darstellt mit Radius R und alle x innerhalb dieses Radius konvergieren und außerhalb divergieren (zusätzliche Randbetrachtung zudem) verstehe ich schonmal.

Der Entwicklungspunkt bzw. der Kreismittelpunkt wäre hier 1/2 richtig? (Form: x-x0)^n
Liegt dann quasi der Entwicklungspunkt einer reellen Potenzreihe auf der x-Achse während bei der imaginären Potenzreihe der Entwicklungspunkt im Imaginären liegen kann?

Hier in dem Beispiel bekomme ich einen Radius von 1/2. Ist es also richtig, mir vorzustellen, dass der Kreismittelpunkt auf (1/2, 0) liegt und ich mir für die Randbetrachtung die x-Werte x=0 & x=1 anschauen müsste?

Es geht um b)

Habe ich richtig gerechnet?

Hallo,

wie komme ich bei rekursiven Folgen wie der unteren darauf, welche Grenzen ich wählen soll um die Beschränktheit der Folge zu zeigen? Man möchte dies ja zeigen, um danach mit einem Monotoniebeweis zu schlussfolgern, dass die Folge konvergiert. Ich verstehe aber nicht wieso in der Lösung dieser Aufgabe gezeigt wurde, dass 0<= a_n <= 3 immer gilt (wie kommt man auf die 3?)

Ein anderes Beispiel ist diese Folge, wo 1<= a_n <= 2 abgeschätzt wurde, da verstehe ich nicht wie man da auf die 1 kommt - a_n ist ja nicht immer eine ganze Zahl, da könnte es doch theoretisch sein, dass von 2 etwas größer als 1 abgezogen wird, z.B. wenn a_n = 4/5.

Vielen Dank im Voraus

Ich verstehe die Nummer 5 nicht kann mir jemand weiter helfen ?

Was wäre die Bedingung für " hochpunkt auf der y-achse" ? Mein Ansatz: f'(0)=0 und ist die allgemeine Funktionsgleichung hier f(x)=ax²+bx+c?

hoffe man kann alles lesen laut GTR also Taschenrechner ist mein Ergebnis falsch weiß jemand warum?
Beim GTR hab ich den Integral Rechner benutzt

aufgabe 14 a)

Hi,

Studiere Mathematik an der Uni im Erstsemester und hab meine ersten Klausuren Ana 1 und LinA 1 geschrieben. Ich hab in Analysis 1 eine 2,0 & und in Lineare Algebra 1 eine 3,0. Mit Analysis bin ich zufrieden, doch Lineare Algebra 1 entsetzt mich, denn das kann ich eigentlich viel besser. Ich hab auch in der Klausureinsicht gesehen, ich habe dumme Fehler gemacht und kann mir das nicht verzeihen. Nun wollte ich einmal fragen, ob ich die Klausur wiederholen dürfte (allgemein gesehen) und ob sich das lohnt? Ich würde mich auf Meinungen freuen.

LG

Hallo, ich habe hier eine Aufgabe, bei der ich nicht weiterkomme:

a) Funktion beschreibt für x≥0 die Konzentration eines Medikaments im Blut eines Patienten mit x in Stunden ab der Einnahme des Medikaments und f(x) in mg pro Liter Blut. Bestimme den Zeitpunkt, an dem die Konzentration am höchsten ist. Gebe die Zeitpunkte an, an denen der Anstieg der Konzentration am größten bzw. der Abbau der Konzentration am stärksten ist.

b) Das Medikament wirkt, wenn die Konzentration im Blut mind. 1,5 mg pro Liter Blut beträgt. Gebe die Wirkungsdauer des Medikaments an.

Für a) habe ich mir überlegt, dass wenn nach der "höchsten Konzentration" gefragt ist, dass ich einfach f(x) ableite, sodass ich den Hochpunkt kriege. Aber dann weiß ich ehrlichgesagt nicht, was das mit "Abbau der Konzentration" gemeint ist.

Für b) weiß ich nicht..

Hallo, ich brauche hier dringend bei der Aufgabe Hilfe:

Bei Temperaturen zwischen 15°C und 45°C finden Salmonellen in Lebensmitteln ideale Voraussetzungen für ihr Wachstum. Deshalb sollte man zubereitete Speisen z.B. für eine Party nicht zu lange stehen lassen und schnell im Kühlschrank reintun. Die momentane Wachstumsgeschwindigkeit einer Salmonellenart kann näherungsweise durch die Funktion f beschrieben werden, dabei wird t in Stunden angegeben und f(t) gibt die Anzahl der Salmonellen pro Stunde an.

a) Bestimme 3 Stammfunktionen F von f und erläutere deren Bedeutung für den Sachzusammenhang.

b) Angenommen, eine Speise wird auf einer Party angeboten und enthält zu Beginn (zum Zeitpunkt t=0 ) etwa 600 Salmonellen der oben beschriebenen Art. Gebe die passende Stammfunktion F für diesen Anfangswert an.

c) Berechne mithilfe des Ergebnisses aus b) die Anzahl der Salmonellen in der Speise nach 5 Minuten, 10 Min, 15 Min, 20 Min.

Ich habe jetzt mehrere Fragen: 1. Wozu braucht man hier überhaupt Stammfunktion auszurechnen (na gut, das ist auch Aufgabe a) ) und 2. Was bedeutet hier in der Aufgabe "momentane Wachstumsgeschwindigkeit"?

Ich hab in Mathe diese Aufgabe bekommen, und da ich leider nicht gut in Mathe bin, versteh ich die Aufgabe nicht. Vielleicht kann mir die ja einer von euch erklären. Danke:)

Ich soll die scheitelpunktform und die produktform angeben. Die scheitelpunktform habe ich durch die scheitelpunktberechnung heraus, richtig?? Und wie berechnet man die produktform?? Lg.

Ich verstehe nicht was mit dem rot markierten Ausdruck gemeint ist.
Die Tabelle verstehe ich auch nicht so ganz , kann es mir bitte jemand erklären ?

Hallo beisammen es geht um folgende Aufgabe c) und d) nr 9

ich weiß dass a richtig und b falsch ist aber was ist mit c und d ???

Hallo zusammen, ich wollte euch mal fragen wie man am sinnvollsten eine Hyperbel zeichnet. Gegeben ist folgende Funktionsgleichung und schon die Lösung. Mit einer Wertetabelle konnte ich es umformen zu z1=+-(z2+2) aber die Punkte einzuzeichnen ist ziemlich ekelhaft...
Ich habe ehrlich gesagt noch nie was mit Hyperbeln am Hut gehabt... :D

Guten Abend,

ich habe noch ein paar Fragen zu folgender Aufgabe und freue mich über eure hilfreichen Antworten.

1. Ich verstehe die Aufgabenstellung nicht so richtig. Man soll ja die Schnittpunkte mit den Koordinatenachsen angeben. Nun habe ich (Bild 1) ja den Schnittpunkt mit der y-Achse berechnet. Dieser ist gleichzeitig Berührpunkt mit der x-Achse, da das Schaubild K die Asymptote a(x) = 1 für x -> minus unendlich hat und für x -> plus unendlich gegen plus unendlich (in den 1. Quadranten) geht. Dieser Punkt ist aber ja kein Schnittpunkt mit der x-Achse, sondern nur ein Berührpunkt. Muss ich diesen nun auch als Lösung angeben oder nicht?
2. War meine Berechnung auf Bild 3 überhaupt notwendig, um zu zeigen, dass es keine weiteren Punkte mit der x-Achse gibt?
3. In diesem Fall habe ich darauf getippt, dass die Asymptote die Gleichung a(x) = 1 ist, was in diesem Fall auch richtig ist. Aber was ist die genaue Regel beim bestimmen einer Asymptote? Immer das letzte x ohne Exponent (falls es eins in der Funktion gibt) mit der letzen Zahl einer Gleichung ohne x (falls es diese gibt) einer e-Funktion?

[Bild 1]

[Bild 2]

[Bild 3]

[Bild 4]

Hallo,

wie bestimmt man die fehlende Intervallgrenze des Intervalls [a; b] und die mittlere Änderungsrate der Funktion f, wenn…

1. f(x) =0,5x+5; f(b)-f(0)=1,5; [0;______]

Ich komme mit der Aufgabe leider nicht so recht weiter.

Um eine Vollständige Induktion durchzuführen, müssen die allgemeinen Rechengesetze richtig sitzen, leider habe ich da eine Lücke.

Wäre mir jemand beim Induktionsschritt behilflich? Den IA und die IV hab ich bereits.

Mit A(n) -> n+1 komme ich auf

 bzw. auf



Wird in der a) darauf abgezielt, dass man neben der Ableitung noch den Index verschiebt? Hat die Summe da was mit dem Entwicklungspunkt zutun? Also wenn z.B. der Entwicklungspunkt x=0 ist, dass die Summe dann bei k=0 beginnen muss?

Bei einem Volksfest wird die Zustromrate durch die Funktion z(t)=−24t^2+190t+500 und die Abstromrate durch die Funktion a(t)=−7,8t^3+78t^2 bestimmt. (t: Zeit in Std. seit 12.00 Uhr; z,a: Zu-bzw. Abstromrate in Besucher/Std.)

Ich bin mir bei der d) unsicher. Den rest habe ich der Vollständigkeit halber trotzdem mit aufgeführt.

a) Stellen Sie die Graphen von f und g für 0 ≤t ≤10 dar (GTR erlaubt).
Lösung vorhanden

b) Zu welchen Zeitpunkten sind die Raten maximal, wann sind sie gleich ?
Lösung: maximale Rate: Ableitungsfunktionen jeweils 0 setzen ergibt bei z(t) einen HP(95/24 / 21025/24) sowie bei a(t) einen TP(0/0) und einen HP(20/3 / 1122,56)
gleiche Rate: a(t)=z(t) bzw. -a(t)=z(t) ergibt t=10 --> Raten sind um 22:00 Uhr gleich

c) Wie viele Besucher hatte das Volksfest insgesamt?
Lösung: Integral von 0 bis 10 von z(t) dt ergibt 6500 Besucher

d) Wie groß ist die maximale Zahl von Besuchern, die sich gleichzeitig auf dem Volksfest befanden?
Ansatz: Hierzu hatte ich schon einiges in anderen Foren gelesen, aber bin trotzdem noch sehr unsicher. a(t) und z(t) geben Änderungsraten an, also muss ich für die Gesamtanzahl der Besucher die Stammfunktion bilden von z(t)-a(t) und davon dann das Extremum berechnen, was wieder bedeutet, dass ich einfach die Nullstelle ausrechne mit z(t)-a(t)=0 oder?
Sprich: z(t)-a(t)=0 ergibt t1=-1,42416, t2=4,50108, t3=10, Die Ableitung von z(t)-a(t) ergibt für t1=527,989 (TP), t2=-254,143 (HP), t3=490 (TP), somit setze ich t2 in meine Stammfunktion (Integral von z(t)-a(t) dt) und komme auf 1875,12 Besucher.
Ist dieser Weg richtig oder hat jemand noch weitere Hilfestellungen für mich?

e) Zeigen Sie, dass insgesamt alle Besucher das Fest wieder verließen.
Lösung: Integral von 0 bis 10 von a(t) dt ergibt 6500 --> Alle Besucher (siehe Lösung c) mit 6500 Besuchern insgesamt) verließen das Fest wieder

Ein leerer, offener Guterwagen (Länge L = 10 m, Masse M0 = 6 000 kg, Geschwindigkeit v0 = 18 km/h) rollt antriebslos unter einer Beladevorrichtung hindurch, bei der senkrecht von oben aus einem großen Vorratssilo kontinuierlich Sand auf die Ladefläche fällt. Die Fördermenge des Sands beträgt α = 1 500 kg/s.
(a) Gib zunächst den allgemeinen Ausdruck für v(t) an.
(b) Berechne nun die zuruckgelegte Strecke s (t) und überlege dir daraus eine ¨ Bedingung fur die gesamte Beladungszeit T0. Welche Geschwindigkeit hat der Wagen nach dem Beladen? (Bitte zuerst den allgemeinen Ausdrack angeben und dann erst Zahlen einsetzen.)

Jensek81'scher Ansatz

a) p M (t) * v (t) = const
M (t) = Mo + α * t
Mo * vo = Mt () * v (t)

=> v(t) = (M0*v0) / M (t)

??
b) s (t) = ∫ v (t) dt = vo ∫ Mo/MO + α t

Aus Hinweis ∫ 1/1+ct dt = 1/c ln (1 + ct) => ∫ Mo/MO + α t = 1/α ln (1 + α t)
=> 18 km/h * 1/1500 ln (1 + 1500 kg /s) = 0,0877

Beladungszeit: 1/2 a To² = L
=> T0 = √ 2 L/a

Geschwindigkeit nach Beladung v0 + a * T0
18 km/H + a * √2L/a

Mit freundlichen Grüßen,

Dr. Hanna Hüngerchen
Gestalterische Genetikerin

Hey, ich bin weit gekommen, aber irgendwie weiß ich trotzdem nicht wieso es falsch ist, wenn ich für K mein Ergebnis einsetze.

Hallo Leute

Der Graph von ha schließt mit den beiden Koordinatenachsen und der Geraden x = 1 im 4. Quadranten eine Fläche ein. Rotiert diese um die x-Achse, so entsteht ein Rotations-körper. Für welches a hat dieser Rotationskörper ein Volumen von 2 m?

Ich verstehe nicht welche Fläche hier gemeint ist. Kann mir jemand bitte helfen

Dankeschön

Hallo zusammen, ich verstehe nicht wie man bei der Randbetrachtung auf den rot markierten Teil kommt. Wieso nehme ich den Betrag der Potenzreihe und wieso =1?
Vielen Dank

Ich verstehe nicht wie mein Professor von (7+1)*8^n-1 zum nächsten schritt gekommen ist und warum er 8 in 7+1 umgeschrieben hat

da nimmt man ja das harmonische Mittel, aber wieso geht das nicht

Wie löse ich die aufgabe?

A) Punkte A, C und B verwenden und durch lineare Gleichungssystem Funktion des 2. gerades bestimmen(oder des 3.?!?!!?)

B) lokales Maximum Dieser Funktion bestimmen und Abstand zur blauen Linie und des Maximums bestimmen.

Nähert sich hier der Graph von unten oder von oben an die schräge Asymptote? Und wie kann man das an den Funktionsterm erkennen?

Kann mir jemand helfen, kann niemanden sonst fragen ob mein Beweis richtig wäre.

Zu beweisen ist: Ist (an) eine positive reelle Nullfolge, d.h Lim(n->∞)an=0, so geht (an)^(-1) bestimmt divergent gegen ∞.

Mein Beweis: Wenn (an) eine positiv reelle Nullfolge ist, dann ist (an) kleiner als jedes beliebige positives Epsilon= ε , was heißt das man (an)^(-1), was 1/(an) ist, durch 1/ ε  ersetzen kann. Da man nun Epsilon beliebig klein machen kann, kann (an)^(-1), nun beliebig groß werden und da (an)^(-1) nur positive werte hat, kann man dann von einer bestimmten Divergenz gegen Plus Unendlich ausgehen.

Hallo, wie komme ich denn auf das richtige Argument? Ich habe euch meine Rechnung abgetippt. Was mache ich falsch??

Es geht um Aufgabe c) für den Eigenraum des Eigenwerts Pi.
Wie bekomme ich denn da eine Nullzeile rein? Ich bekomme dass nicht verrechnet.

beim zweiten beispiel von a) habe ich keine ahnung wie man das auflösen soll. Weder photomath noch geogebra kann das lösen

Hallo Leute,

ich übe gerade Kopfrechenaufgaben. Folgende Aufgabe:

Kann mir da einer weiterhelfen?

Alex

Hallo,

ich benötige Hilfe bei folgender Matheaufgabe:
Gegeben ist die Funktion fa(x) = (2 – a ∙ cos(x)) ∙ sin(x) für x ∈ ℝ und a > 0
a.) Es sollen zunächst von a unabhängige Nullstellen berechnet werden.
b.) Danach soll man die Werte von a ermitteln, sodass fa weitere Nullstellen als die von Teil c) besitzt
Ich stehe komplett auf dem Schlauch. Könnte mir jemand eine Lösung geben und ggf auch erklären, sodass ich es nachvollziehen kann. Danke

Wie löse ich diese Aufgabe?

f(2)=4, 8a+4b+2c =4

f(0)=0 d=0

f'(2)=0, 12a +4b +c = 0

Und wie mache ich dann die b?

Aufgabe b)

Wie bestimme ich die ganzrationale funktion?

Hallo,
ich verzweifle grad daran ob es einen Zusammenhang zw. der Kathete und der Hypothenuse in einem gleichschenkligem rechtwinkligem Dreieck gibt? Also wenn die Kathetenlänge 1 ist ist die Hypotenuse ja laut Satz des Pythagoras Wurzel 2.
Aber wenn die Kathetenlänge x ist wie viel ist die Hypotenuse im Zusammenhang mit x?
Vielen dank schonmal! :)

Hey, kann mir einer sagen was 2k' in Bezug auf folgendes bedeutet? Also das ' verwirrt mich.

Danke!

Hallo Zusammen, ich bräuchte Hilfe bzw. die Lösungen für folgende Aufgaben (a hab ich schon gemacht), da ich einfach nicht mehr weiterkomme :( Danke!

Hey, bei dem folgenden Beispiel werden die Intervalle nach den Nullstellen her eingeteilt. Dadurch wird dann bestimmt, welche genaue Monotonie es im welchen Intervall hat. Meine Frage ist es nun, ob man die Monotonie mit dieser Einteilung (nach den Nullstellen) auch so lösen kann, wenn der gezeichnete Graph nicht vorab gegeben ist, wie hier? Der Graph, also die Zeichnung, muss für diese Methode gegeben sein, oder?:

Vielen Dank.

A einem Heißluftballon wurde die Flughöhe protokolliert. Bestimmen Sie die Höhendifferenzen und die mittleren Anderunesraten.

Und Aufgabe B Entscheiden Sie anhand der mittleren Änderungsraten, in welchem Zeitintervall der Heißluftballon am schnellsten gestiegen bzw. gefallen ist.

das verstehe ich nicht wie man da vor geht

Ich komm da nicht weiter wie kann ich sehen wo der Luftballon am schnellsten war kann mir wer helfen

Wie bestimme ich die ganzrationale funktion bei a)

Bedingungen: f(0)=1, f'(0)=0, f'(1,5)=0, f(1,5)=0 (hier bin ich mit unsicher)

Wie löse ich dann das gleichungssystem?

Hey zusammen :) kann mir jemand bei der Teilaufgabe B weiterhelfen. Wie kommt man auf das Ergebnis mit dem Taschenrechner und wie lautet der Ansatz? Lösungen sind auch unten angegeben. Die helfen mir jedoch leider nicht weiter xD

Hallo,

es geht um die Aufgabe d. Wie kommt man darauf? Ich hätte jetzt versucht das lineare Gleichungssystem in Abhängigkeit von alpha in die Stufenform zu bringen und und dann zu schauen, für welches alpha ein Widerspruch entsteht, aber ich vermute der Weg ist zu aufwändig. Hat jemand Ideen / Tricks?

Wie macht man die a ?

Bedingungen : f(0)=3, f'(0)=0, f''(3)=0

Aber wie löse ich dann das gleichungssystem das da entsteht?

Hallo,

kann mir jemand das, was in diesem Abschnitt beschrieben ist, nochmal in eigenen Worten erklären?
Ich verstehe nämlich nicht, warum es überhaupt zu jedem Punkt auf dem Einheitskreis einen negativen Winkel ß gibt????
Und warum ist ß=a-360Grad????

Und was ich erst recht nicht verstehe ist, warum dann sin (360Grad+a) positiv ist und der cosinus (360Grad+a) auch???

Meine Skizze:

Kork ist ein besonders leichtes Material.

1. Kannst du eine Kugel aus Kork mit einem Durchmesser von 1 m tragen?.
2. Wie groß ist der Radius einer Stahlkugel, die genau so viel wiegt wie die Korkkugel

Ich fühle mich gerade richtig dumm, weil ich nicht blicke wie man den Mist ausklammern soll zu (n+1)+(n+2)

Weder Daniel Jung noch ChatGPT konnte mir helfen.



Könnte bitte jemand überprüfen, ob meine Ergebnisse stimmen?

Wie bestimme ich hier die empirische Standardabweichung dieser Daten?

Einen wunderschönen guten Abend,

ich habe noch ein paar Fragen zu folgender Aufgabe. Im folgenden befindet sich ein Bild der Aufgabe und ein Bild des Lösungsvorschlags. Danach befinden sich meine Fragen (meine Fragen beziehen sich ausschließlich auf Aufgabenteil (1)).

Ich habe bei der Aufgabe alles bis auf den Aufgabenteil (1) perfekt verstanden. Hier sind meine Fragen zu dem Aufgabenteil (1):

1. Wie kann man anhand eines gegebenen Schaubildes bestimmen, welchen Grad die Funktion haben muss? Geht das nur, indem man sich die Wendepunkte anschaut?
2. Das habe ich denke ich jetzt verstanden (die Fragen waren nur mein Gedankengang): Warum kann man sagen, dass wenn es wie hier beim gegebenen Schaubild vier Wendepunkte gibt, dass es keine Funktion vierten Grades sein kann? Ich verstehe, dass wenn man eine Funktion vierten Grades zweimal ableitet es nur noch eine Funktion vom Grad zwei ist. Aber wieso kann man aus der zweiten Ableitung, welche in diesem Fall Grad 2 ist (bei einer ursprünglichen Funktion vierten Grades) daraus schließen, dass sie keine vier Wendepunkte haben kann? Weil die Ableitung also nur maximal zwei Ergebnisse haben kann. Also müsste in diesem Fall die Funktion mindestens von Grad 6 sein, um zum abgebildeten Schaubild zu passen.
3. Gibt es noch eine andere Möglichkeit, um eine solche Aufgabe wie hier beantworten zu können, ohne auf die Wendepunkte einzugehen?
4. Ist dieser Lösungsweg wie hier in dem Lösungsvorschlag der einfachste?
5. Inwiefern haben die gemeinsamen Punkte einer Funktion mit der x-Achse einen Zusammenhang mit dem Grad einer Funktion?
6. Inwiefern haben die maximal möglichen Punkte einer Funktion mit der x-Achse einen Zusammenhang mit dem Grad einer Funktion?

Ich freue mich über eure hilfreichen Antworten.

Hi! Wie vereinfache ich diesen Bruch, ich kapiere den rechenweg nicht so ganz, kann das jemand die Rechenschritte aufschreiben.

Muss (n+1)^k < n^k+1 + n^k beweisen für alle n,k aus den natürlichen zahlen. K ist beliebig und immer fest für alle n. Wollte das mit Induktion beweisen jedoch weiß ich nicht wie ich zu Induktionsvoraussetung zurück komme wenn da (n+2)^k steht, denn ich muss den therm zu (n+1)^k umformen um die Voraussetzung anwenden zu können. Danke im Voraus für eure Zeit und Antworten :D

Wie löst man dieses Aufgabe

Hallo,

ich habe Probleme damit zu verstehen wann man welche Formel (im Bild blau und rot) für die Fehlerfortpflanzung verwenden kann. Wie man im Bild erkennt lassen sich diese Formeln so gar in dem Fall (zur berechnung von p=mv) ineinander umformen. Bei anderen Formeln wie z.b. Rges = ((R1 + R2)/(R1*R2))^-1 geht das allerdings nicht.
Wann also verwendet man welche Formel?

Danke:)

Kann jemand diese Gleichung lösen? Bitte Schritt für Schritt

Höhere Mathematik- Vorbereitung für die Universität

Die Schar lautet -ax^2 +10ax -9a für a größer 0.

Wie ermittele ich a so dass der graph der Schar die gerade y=1,6x berührt?

Klar, es gilt f'(x)= g'(x) und f(x) = g(x) aber wie wende ich das konkret an

Unter anderem ist die Wendetangente y=-8/5x+5 gegeben. Ich habe schon die Bedingungen f’(5)=-8/5 daraus entnommen, mir fehlt aber noch eine Bedingung. Was kann ich daraus noch feststellen? Danke im voraus

Die funktionenschar lautet: - (x^3 -3ax^2) / 144

Ich soll zeigen dass alle extrema des graphen auf dem graphen der funktion - 1/288 *x^3 liegen.

Klar ich bestimme die extrema sund dann ihre ortskurve

Das problem ist dass ich nicht die extrema berechnen kann. Wie mache ich das? Ich bekomme einmal (0/0) und einmal (-2a/ - 7a^3/72)

Hallo, ich möchte diese komplexe Gleichung mittels Mitternachtsformel lösen. Die Gleichung habe ich gedanklich schon nach 0 umgestellt und eingesetzt. Ist das Vorgehen falsch? Ich komme so leider nicht auf die Lösung, wie man auf dem unteren Bild sieht.

Wie löst man diese Aufgabe

Meine Dozentin hat irgendwas gerechnet, aber ich weiß nicht, was sie hier genau gemacht hat.

4 + 3 = 3 mod 6

-4 + 4 + x = 3 - 4

x = -1

x = -1 = -1 * 6 + 5

= 5

L = {5} Z_6 eind. Lösung

oder

5x = 2 mod 12

5x = 2 = 2 + k * 12

x = (2+ 12 * k) / 5 = 2/3 = 14/5 = 3P / 5 = 50 / 5 = 10

L = {10} Z_12 eind. Lösung ggT(5; 12) = 1

Bitte Hilfe!

Hallo,

wie erhält man die allgemeine Lösung von Differentialgleichungen und welche Schritte muss man durchgehen?

Kann mir jemand es anhand dieser Beispiele zeigen:

1) x'=3x

2) x'=(t²+1)x

3) x'=sin(t)x

Ich danke in Voraus.

Die funktion lautet x^3 - 2ax^2 + a^2x

Bestimme a so dass es einen tiefpunkt an der stelle x= -1 gibt

Mein Ansatz ist die ableitung zu bilden und die extrema zu bestimmen aber was dann????

Richtige Lösung: -25 = -5 * 6 + 5 => -25 = 5 mod 6

Aber wieso nicht -25 = -4 * 6 - 1 => -25 = -1 mod 6 ?

Könnt ihr mir schritt für Schritt bei der c die wendetangente berechnen?

Wie macht man das?

z.B. das multiplikative Inverse von 3 in Z₇ finden.

Dann heißt das doch folgendes

3 * x^-1 = 1 mod 20

Wie kommt man denn auf das richtige x ?

Ich kenne ja die Funktion hier, aber man kann die Funktion nicht mitten in einem Satz benutzen. Viele hier können die mathematischen Schreibweisen irgendwie mitten im Satz und kleiner schreiben. Wie macht ihr das?

wie irrational ist die eulersche zahl

Kann mir jemand helfen bei den Aufgaben und mir erklären wie man den Kölner Dom in das dreidimensionale Koordinatensystem zeichnen kann.

Habt ihr Ansätze für diese Aufgabe? Ich habe ehrlich gesagt keine Ahnung wie ich die angehen soll.

Guten Abend,

Ich hatte zwei Fragen bezüglich dieser Aufgabe

1. Wie wurde der Zähler hier faktorisiert mit den Binomischen-Formeln? bei dem Nenner ist mir es klar.
2. Die Zweite Frage wäre, warum an der markierten Stelle ein minus ist, was für mich Sinn ergeben hätte, wäre wenn der Bereich anstatt -3<x<2 , x<-3 v x<2 und somit ein negatives Zeichen daraus resultiert weil wir beide stellen jeweils von der linken bzw. kleineren Seite betrachten würden. Ich habe da anscheinend ein Denkfehler, könnte mich jemand bitte da aufklären?

Aufgabenstellung:

Lösung zu der Aufgabenstellung:

Kann man das voraussagen, ohne dieses Integral berechnen zu müssen? Durch das x^2 ist die Anwendung von partieller Integration bzw. Substitution recht aufwändig.
Gibt es da einen Trick?

Die a habe ich schon da kommt a für x Raus.

Ich brauche aber hilfe bei der b. Ich verstehe nicht wie das geht weil je nachdem was a ist kann es ja ein HP oder TP sein

Ich habe die funktionenschar

 Ich soll die gleichung der ortskurve der Hochpunkte berechnen

Meine Lösung: HP ( wurzel 2a / - 1/a^2)

Die Ortskurve lautet:

 Stimmt es?

Klar, bei der a) einfach Zeigen dass die steigung gleich ist an den Anschlussstellen ist und den wendepunkt berechnen.

Aber wie mache ich die b?? Mein ansatz: Funktion muss die gleiche steigung wie bei der a haben und einen WP?

Die funktion lautet x^2 + kx - k

Für welche k gibt es 2 Nullstellen und für welche keine?

Klar, wenn die funktion größer 0 ist keine und wenn kleiner 0 dann 2. Aber wie mache ich dann weiter?

Kann mir das jemand erklären :)

Aber wie?



Guten Abend,

ich benötige bei der Aufgabe noch ein wenig Hilfe.

1. Leider verstehe ich die Begründung noch nicht so ganz, wieso K immer oberhalb der Asymptote verläuft. Dort steht ja in dem Lösungsvorschlag folgendes: „Wegen e^-x > 0 für alle xeR liegt K oberhalb der Asymptote.“. Über eine genaue Erklärung von euch würde ich mich sehr freuen.
2. bei der Berechnung der Extremstellen bin ich auf x = -ln(1/2) gekommen, was laut meinem Taschenrechner das gleiche wie x = ln(2) ist. Wieso ist das das gleiche? Ist meine Angabe von x = -ln(1/2) als Nullstelle schlechter als die Angabe in der Lösung von x = ln(2)? Wie kommt man überhaupt darauf, dass -ln(-1/2) das gleiche wie ln(2) ist?

Kann mir winer bitte bei den Aufgaben helfen🙏🏼🙏🏼

Ich komme nicht darauf, wie das gehen soll. Kann mir da jemand helfen?

Die funktion lautet x^3 -2 ax^2 + a^2x

Wie bestimme ich a so, dass es einen tiefpunkt an der stelle x= -1 gibt?

Nehmen wir mal an, ich untersuche eine reelle 3x3 Matrix. Nun möchte ich den Eigenraum für einen Eigenwert berechnen und löse nach Gauß. Ich erhalte zwei Nullzeilen. Dann besteht meine lineare Hülle aus zwei Vektoren.

Nun meine Frage: Die zwei Vektoren, die ich als Lösung erhalte sind noch keine Eigenvektoren oder? Sie bilden nur in der Linearkombination einen Eigenvektor oder? Ich verstehe das noch nicht so ganz.

Was wird hier verlangt und was ist die Erklärung für das Verfahren?

Danke im Vorraus

PS: ich hasse Geometrie

Aufgabe 1 und 2 haben wir Aufbekommen und ich sitze schon den ganzen Tag dran auch meine Mitschüler wissen nicht was zu machen ist weil keine Funktion vorgegeben ist. Kann uns da bitte je,and hel%n wie muss man hier vorgehen?