Parameter K finden?
Hey, ich bin weit gekommen, aber irgendwie weiß ich trotzdem nicht wieso es falsch ist, wenn ich für K mein Ergebnis einsetze.
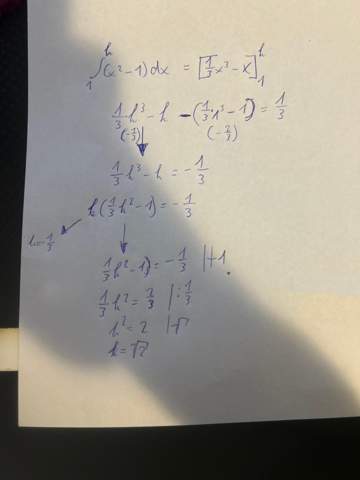
3 Antworten
Der Schritt ab k(1/3k^2 - 1) = -1/3 ist falsch. Das kannst du nur machen, wenn rechts vom "=" eine 0 steht. Anstatt aufzulösen, könntest du 1/3 auf beide Seiten von 1/3k^3 - k = -1/3 addieren, um 1/3k^3 - k + 1/3 = 0 herauszubekommen.
Jetzt kannst du ganz einfach das Newton-Raphson-Verfahren auf das Polynom 1/3k^3 - k + 1/3 = 0 anwenden. Das sollte trivial sein. Dabei müsstest du, falls du keinen Fehler machst, den Wert 0,34729 herausbekommen. Anschließend kannst du eine Polynomdivision mit diesem Wert ausführen. Diese würde dann so aussehen:
(1/3k^3 - k + 1/3) / (k - 0.34729) = ...
Dabei kommst du dann noch zusätzliche auf die Werte: 1,53208 und -1,87938.
Also sind die Lösungen: 0,34729, 1,53208 und -1,87938.
Da die untere Grenze des Integrals 1 ist, muss die obere Grenze größer sein. Also ist die einzige noch mögliche Lösung 1,53208
Du kannst da nicht einfach sagen h=-1/3, sondern musst du die Nullstellen vom Polynom 1/3*h^3-h+1/3
Du kannst dir die Lösungen für deine Gleichung hier ansehen:
1/3*k^3-k=-1/3 lösen | Microsoft-Matheproblemlöser
Ich glaube aber, dass du die Aufgabenstellung falsch abgeschrieben hast, weil das mit Schulmathematik nicht lösbar ist.
Bis Zeile 3 ist bei dir alles richtig, danach wird es falsch. Ich bin mir aber sicher, dass du die Lösung bei korrekter Aufgabenstellung ganz leicht gefunden hättest.
Hoffe, das hat geholfen :)
Ich wollte einer Klassenkameradin aus dem Parallelkurs helfen. Aber ich kam hier nicht weiter. Ich habe die Aufgabenstellung korrekt abgeschrieben. Wir gehen in die 12. Klasse 😅