Umkehrfunktion einer Tangente an einen Graphen berechnen ohne die Umkehrfunktion des Graphen zu verwenden?

Guten Tag, bei der Aufgabe c) soll ich die Unkehrfunktion der Tangente t an f(t) angeben ohne die Umkehrfunktion von f(t) zu benutzen.

Mein erster Gedanke war einfach die tangentengleochung umzukehren, zwar war es richtig aber stand als weitere Möglichkeit nicht drinnen. Was ich nicht verstehe ist wie man auf die Steigung von der Umkehrfunktion von t kommen soll.

Zwar steht das hier:

aber wenn ich die Punkte (0|3/8) und (4|4) einsetze kommt immer was falsches raus immmmmer egak ob ich unten y und oben y hab egal ob ich x als y verwende und y als x ich komm immer auf etwas falsches. Daher wollte ich fragen ob mir jemand evt den Schritt bezüglich dem Errechnen der Steigung nochmals erklären könnte?

Answer 1

[evtldocha]

aber wenn ich die Punkte (0|3/8)

Der Punkt ist ja auch falsch. Aus dem Achsenabschnitt der Tangente wird bei der Spiegelung an der Winkelhalbierenden die Nullstelle der Tangente an die Umkehrfunktion:

Achsenabschnitt der Tangente: $t\left(0\right)=\frac{3}{8}\cdot0+\frac{5}{2}=\frac{5}{2}$

Damit hat die Tangente an die Umkehrfunktion die Nullstelle N(5/2 | 0) und die Tangentengleichung ergibt sich aus den beiden Punkten P(4|4) und N(5/2| 0)

$\overline{t}=\frac{4-0}{4-\frac{5}{2}}\cdot x\ +b=\frac{8}{3}\cdot x+b$ $\overline{t}\left(4\right)=\frac{32}{3}+b=^{\left(!\right)}4\ \to b\ =4-\frac{32}{3}=-\frac{20}{3}$

Also hat die Tangente er Umkehrfunktion die Gleichung: $\overline{t}\left(x\right)=\frac{8}{3}x-\frac{20}{3}$

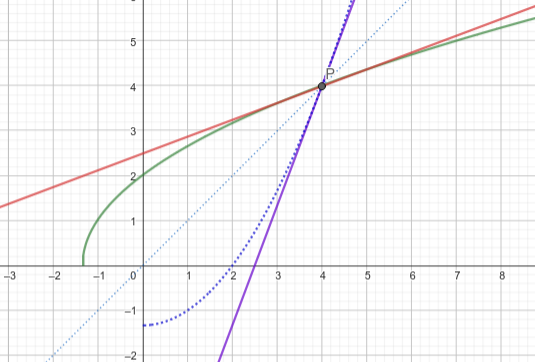
Skizze: