Kann jemand mir die Relativitätstheorie von Galilei simpel zusammenfassen ?

Hier sehen wir die visuell wahre Raumzeitkrümmung eines Masseobjektes. Jedoch frage ich mich hier, wie denn die Geodäte hierbei verläuft.

Man hat ein Raumschiff mit der Länge 6m und eine Garage mit der Länge 5m. Bei 4 Metern in der Garage gibt es eine Markierung. Das Raumschiff bewegt sich mit zb 0.9c in die Garage hinein, sobald es die Markierung berührt schließt sich die Garagentür.

Da bei einem Beobachter das Raumschiff kontrahiert wird, ist es kürzer und passt somit hinein. Beim Inertialsystem des Raumschifffahrers passt es nicht komplett hinein, da sich die Garage noch mehr verkürzt.

Führen wir nun das Gedankenexperiment weiter. Sobald das Raumschiff die Markierung berührt, stoppt das Raumschiff sofort ( oder sehr sehr schnell ) und alles kehrt in seine original Größe zurück.

Für einen Beobachter ist das Raumschiff nun in der Garage und da es größer wird gibt es mechanische Schäden an der Vordergrund Rückseite des Raumschiffes.

beim Inertaialsystem des Raumschifffahrers schließt sich die Tür später aufgrund der Relativität der Gleichzeitigkeit und wenn es sofort stoppt , kehrt alles in Original Größe zurück. Nun gibt es doch Schäden am Dach des Raumschiffes, da die Garagentür darauf fällst und da es nicht eingeschlossen wird, wird es doch keine Schäden an der vorder und Rückseite des Raumschiffes geben.

Ist das nun nicht ein Paradox, da es verschiedene Schäden in verschiedenen Inertialsystemen gibt ?

Hallo, ich bringe mir gerade die Zeitdilatation und Längenkontraktion der speziellen Relativitätstheorie selber bei. Nun habe ich zwei Fragen. Die erste lautet:

Erstens aus der Sicht eines schnell bewegenden Objektes, wie sieht die Außenwelt aus für ihn? Müsste er nicht alles in schnellerer Geschwindigkeit sehen?

Zweitens ich habe das Thema mit der Längenkontraktion noch nicht ganz verstanden. Ich bin soweit, dass ich weiß, dass wenn sich ein schnell bewegendes Objekt an uns vorbei bewegt dann scheint es für uns verkürzten d.h. es braucht unser Initials System weniger Zeit als in seinem eigenen Initials System aber warum ist es so?

Laut der Zeitdilatation vergeht doch in sich schnell, bewegen, dem System die Zeit langsamer d.h. ja, dass eine Aktion für ihn ausgesehen, kürzer braucht aber für einen Beobachter länger braucht heißt das dann nicht auch, dass die Aktion vom Schnell bewegen kürzer braucht von seiner Perspektive aus als für uns aber das wäre ja ein Widerspruch?

Mein Physiklehrer hat diese Frage nicht verstanden, darum frage ich sie hier. Nach der klassischen Physik wie Newton sie formulierte, kann die Geschwindigkeit eines Objeks nur in Relation zu anderen Objekten bestimmt werden. Einstein wies diese Vorstellung zurück und zeigte auf, dass Raum, Zeit und Masse miteinander verknüpft sind. Ein Masseloses Teilchen bewegt sich immer mit Lichtgeschwindigkeit. Und nun zur Frage: können wir denn nicht anhand der Ausbreitungsgeschwindigkeit des Lichts sagen wie wie uns relativ zum Raum bewegen. Alternativ könnte man auch einen Punkt finden an dem die Zeit am schnellsten vergeht. So könnte man doch auch sagen, wie sich die Erde, ein Punkt auf der Erde oder auch jedes andere Objekt im Sonnensystem und darüber hinaus relativ zum Raum bewegt, oder nicht?

In der folgenden Diskussion

Swing-by-Effekt: Ist die Änderung der Bahnenergie eines Raumfahrzeugs relativistisch erklärbar, oder fand man bisher nur noch keine Erklärung?

wurde deutlich, dass die vielen Erklärungsversuche mit physikalisch unseriösen Erklärungen gespickt sind, die zwar als selbstverständlich bagatellisiert werden, aber gerne auf bürgerlich übliche Vorstellungen und Argumente zurückgreifen. Doch kann man in der Physik nicht zaubern, wie z.B. verwandeln, sondern nutzt stattdessen wegen fehlender Kenntnis einer echten physikalischen plausiblen Erklärung sogenannte virtuelle Quanten, um die physikalisch unseriösen Wörter „verwandeln“ oder „transformieren“ nicht benutzen zu müssen. Tatsache ist aber, dass sich bei dem Swing-by-Effekt eine Wirkung umgekehrt proportional im Betrachtungssystem verteilt.

Was dem einen Ort etwas genommen wird,
das wird am anderen Ort dafür zugeführt
und umgekehrt.

Doch handelt es sich hierbei um einen einzigen deterministischen Prozess, der eine vollständig durchgeführte substanzlose Wechselwirkung beschreibt, und nicht um eine Kette von Vorgängen. Die übliche substanzielle Wechselwirkung hingegen bedarf aber einer zeitlichen Abfolge bzw. einer Kette einzelner Prozesse, um in Form eines Quantums vom einen Ort zum anderen zu wechseln.

Die einzige Erklärung für eine substanzlose, unmittelbare Veränderung wäre eine Dimension anstatt einer akausalen Kraft. Denn die Gravitation zeigt ihre Quantität ausschließlich als eine räumliche Wirkung, die wir als Intensität auch ohne Messgerät wahrnehmen können, obwohl wir bisher dachten, nur drei räumliche Dimensionen erfassen zu können.

So ist nun ganz offensichtlich, dass wir real über vierdimensional orientierte räumliche Informationen verfügen, mittels der wir den aktuell räumlichen Zustand erfassen können. Denn die Intensität des gefühlten Gewichts kann man auch als 4. räumliche Dimension verstehen, weil jene quantitative Größe unbedingt eine räumliche Beziehung hegt, die uns als Quadrat der Entfernung bekannt ist.

Auf diese Weise arbeitet sogar unser Unterbewusstsein beim Springen damit und berechnet, wie viel <Kraft> angewandt werden muss, um genau den gewünschten Punkt zu treffen. Jeder Affe, der in den Bäumen herumspringt, tut das, denn wäre dem nicht so, dann wären bereits unsere Vorfahren ausgestorben. Denn wer nicht beim Springen in den Bäumen die Gravitation berücksichtigt, der wird sich bald nicht mehr weitervermehren können.

Also die Intensität des Gewichts ist eine bidirektionale Quantität, die einen räumlichen Abstand in die Tiefe der 4. Dimension darstellt.

Womit nun die zeitliche Dimension die 5. Dimension ist und nicht mehr der deterministischen Bedingung widerspricht, dass nur gleichzeitig gegenwärtige, aber unterschiedliche räumliche Punkte wirken können. Also, das raumzeitliche Vorstellungsmodell ist damit überflüssig, denn die Gravitation ist die notwendige 4. räumliche Dimension.

Der Relativitätstheorie ist es egal, ob du die 4. Dimension als Zeitdauer betrachtest oder als einfachen räumlichen Abstand. Die Relativität behält ihre Gültigkeit bei.

Etwas tiefergehend beschrieb ich das in meinem Kommentar zu Kelec, worauf ich nun diese Diskussion eröffnete. Ich werde aber auch eine eigene Antwort hierauf schreiben, wenn ich die konstruktiven Argumente erfahren habe, denn die meisten Argumente waren bisher eher emotional unsachlich und nicht verwertbar.

Also wer nun einmal wirklich konstruktiv darüber diskutieren möchte, der sollte nun mal zeigen, dass eine konstruktive Diskussion keinesfalls von destruktiven Argumenten zerstört werden kann.

In Physik haben wir eine Hausübung aufbekommen, in der wir die Lebensdauer eines bewegten Myons ausrechnen mussten. Als Angabe hatten wir die Formel delta-t=delta-t0 : (Wurzel aus (1 - (v : c)im Quadrat)). v = 0,999v • c. C ist die Lichtgeschwindigkeit und im Taschenrechner definiert (2,998 • 10hoch 8 m/s). Die Lebensdauer eines stationären Myons an Stationären Uhren beträgt 2,2 mikrosekunden. Die Frage lautet, wie groß die Lebensdauer eines bewegten Myons ist, da sie auf Grund der Zeitdilatation größer sein müsste. Ich habe 5 sehr verschiedene Ergebnisse, glaube aber nicht, dass sie richtig sind. Wie kann ich das berechnen?

Bleibt die Zeit von außen betrachtet an einem Schwarzen Loch absolut stehen? Und wenn ja, müsste sie für einen Beobachter, von dort aus betrachtet, im übrigen Universum (in der Plancksekunde, in der er dort ankommt) nicht unendlich schnell verlaufen?

Ich las bei der Eröffnung einer Diskussion die folgenden Worte:

Du hast einen interessanten Diskussionsansatz, eine steile These oder Tipps und willst wissen, was andere darüber denken? Dann diskutiere mit unserer Community über Dein Thema.

Und jenes Thema lautet bei mir:

Was wäre, wenn sich herausstellte,
dass die 4. Dimension nicht die Zeit,
sondern eine räumliche Dimension wäre?

Aber leider ist das hier im Falle der Physik ein aussichtsloses Unterfangen.
Zur Erklärung, wie ich das verstanden wissen möchte, hier eine kurze Einleitung:

Ich beging mit einer Frage die Ungeheuerlichkeit, zu bezweifeln, dass die 4.Dimension die Zeit wäre, sondern von rein räumlicher Natur ist, und bei der Gelegenheit erwähnte ich auch, dass die Argumente der allgemeinen Relativitätstheorie nicht relevant seien.

So erfuhr ich einen Shittstorm und bin seither ein Wissenschaftsleugner, aber ich frage mich: Gibt es hier nur Experten, die sich als Einstein-Inquisition verstehen, oder gibt es auch unparteiische Normalos mit einem gesunden Gespür für elementare Logik?

Ich weiß, dass man mit Fußballfans besser nicht über konträre Ansichten diskutieren darf, aber dass man auch in der Physik besser nicht über ihre Glaubensbekenntnisse diskutieren sollte – das ist für mich ehrlich gesagt eine neue Erfahrung.

Natürlich gibt es auch eine alternative Erklärung dafür, das Phänomen zu erklären, ohne Einsteins Zeitdilatation als Ursache zu betrachten, die sogar auch deutlich verständlicher und vorstellbar ist. Aber die Experten sind nun mal so konditioniert, es nur unter den zeitlichen Aspekten zu erklären. Denn sie geben ja nur wieder, was sie gelernt haben. Davon abweichen können ja die wenigsten, weil die meisten befürchten müssen, von der selbsternannten Einstein-Inquisition erwischt zu werden, wenn sie etwas anders erklären, als es in der heiligen Doktrin steht.

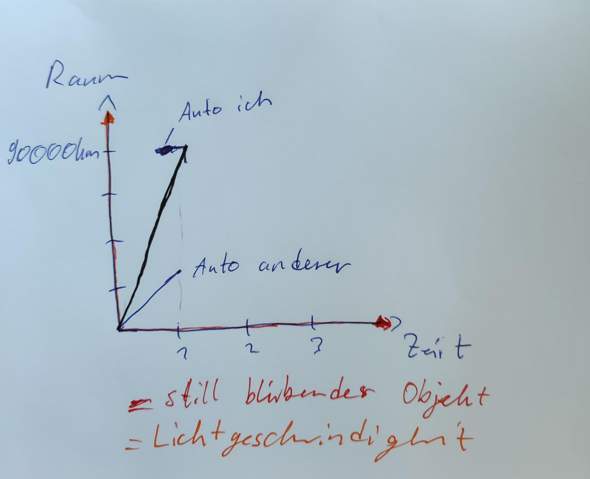
Also, wenn man die Zeit auf der Uhr sieht, dann erfährt man, wie oft am Tag der Stundenzeiger seine Kreise zog, wobei der kleine Zeiger das etwas detaillierter aufschlüsselt, und der Sekundenzeiger es noch genauer macht. Doch versteht auch jeder, dass der Zeiger eine räumliche Strecke zurücklegt, und jene setzen wir der Zeit gleich. Doch ist das nicht dieselbe Zeit, die den Zeit-Punkt bestimmt, sondern es ist konkret eine Ersatzvorstellung von einer räumlichen Strecke, die man auch als Zeit-Dauer bezeichnet.

So gesehen wird der übliche Betrachter die Zeit-Dauer grundsätzlich als „Zeit“ bezeichnen, obwohl er damit die räumliche Strecke meint. Daher kann man auch sagen: Eine Zeit-Dauer ist eine mehr oder weniger lange Strecke. Also ein räumlicher Abstand zwischen zwei Zeit-Punkten – daher der Präfix „Zeit“. Wissenschaftlich sprechen wir von einer Quantität, denn es ist eine numerisch abzählbare Größe.

Aus dieser Sicht heraus handelt es sich in Wirklichkeit nicht um eine zeitliche Größe, sondern um eine räumliche Größe, und damit kann unser Verstand gut umgehen. Denn mehr Zeit bedeuten dann vorstellbar längere Strecken. Wenn dann ein Abstand mehr wird, dann steht das auch im Zusammenhang mit einer längeren Zeit-Dauer. Haben wir es aber mit geringer werdenden Abständen zu tun, dann sprechen wir von einer kürzeren Zeit-Dauer.

Doch im Gegensatz dazu sprechen die Experten bei der Zeitdilatation von einer Dehnung, also einer Expansion, oder simplifiziert: Die Strecke, die wir als Zeit verstehen wollen, wird größer. Und genau in dieser Feststellung liegt das Problem, weil unser Verstand die Formulierung „Dehnung“ als eine größer werdende Zeit-Dauer betrachtet.

Dieses Missverständnis wird vom Willen Einsteins geprägt, die Zeit unbedingt als Ursache zu betrachten, denn wenn man die Konstanz der Lichtgeschwindigkeit einhalten will, müssen die Längen umgekehrt proportional gegenüber der Zeit verändert werden. Also die Strecken kontrahieren, während Zeit dilatiert bzw. expandiert. Dieses ist aber höchst unlogisch, wenn auch die mathematische Beschreibung exakt ist.

Real aber werden Dinge in die Formulierung einbezogen, die überhaupt keine Wirkung beschreiben, sondern vielmehr eine Nichtwirkung, damit die Zeit als Ursache umgekehrt proportional logisch erscheint. Denn letztendlich dehnt sich hier nicht der wirkende Anteil der Zeit, sondern der nicht wirkende Anteil. Demzufolge wird der wirkende Anteil der Strecke kürzer, was man auch als Längenkontraktion versteht.

Denn sowohl die Zeit-Dauer als auch die zurückgelegte Strecke werden kürzer. Jeder versteht nämlich, dass kürzere Strecken auch weniger Zeit-Dauer benötigen. Und wir erwarten daher eine Logik, die nur die Wirkung anwesender Dinge beschreibt und nicht die Beschreibung der abwesenden, nicht wirkenden Dinge.

Damit stehen Raum und Zeit nur in einem proportionalen Verhältnis und nicht in einem umgekehrt proportional ausgleichenden kausalen Verhältnis. Daher bleibt ungeklärt, wohin die Längen verschinden und woher die zeitlichen Mengen kommen.

Wenn wir nun auf die Eingansfrage zurückkommen, dann werden jetzt sowohl die Abstände geringer als auch die Zeit-Dauer. Das bedeutet, dass der Raum kontrahiert, alle Radien der Orbitale der Teilchen in den Atomen kürzer werden und deren Umdrehungszahlen größer werden.

Wenn man nun davon ausgeht, dass das Leben einer Körperzelle ein gewisses Zerfallsdatum hat, das von der Lebensdauer bzw. den inneren Umdrehungen oder der Frequenz der beteiligten Atome bestimmt wird. Dann muss natürlich so manche Zelle früher ausgetauscht werden, was letztendlich als Alterungsprozess angesehen wird.

So wird natürlich auch der Zwillingsbruder, der oben in der ISS sitzt, nur langsam alt, während der Bruder unten auf der Erde viel schneller altert. Denn da oben im All sind die Abstände länger und unten auf der Erde kürzer. Das gleiche passiert, wenn man mit relativistische relevanter Geschwindigkeit bewegt, bei der die Längen nämlich schrumpfen.

So Leute, jetzt erst könnt ihr euch eine eigene Meinung bilden, wie man die Dinge zu deuten hätte, oder einen Beitrag darüber abliefern, was ihr glaubt, an meiner Darstellung falsch wäre.

• Diese Frage ist eigentlich dem Kommentar von SlowPhil geschuldet und wird auch erklären, warum die Zeit für die Relativitätstheorie nicht relevant ist.

Die Raumkrümmung ist eine 4D-Erscheinung, aus einer 3D-Perspektive heraus betrachtet, die heutzutage immer noch nicht wirklich plausibel ist, weil zwar behauptet wird, die Logik des aktuell gültigen Vorstellungsmodells der Raumzeit sei vierdimensional, doch erfolgt die Bewertung einer 3D-Logik, obwohl tatsächlich mathematisch an einigen Stellen 4D-Berechnungen stattfinden.

Somit geht uns offensichtlich einiges verloren, besonders dann, wenn empfohlen wird, auf eine absolute Vorstellung von Zeit und damit auch auf eine plausible Vorstellbarkeit zu verzichten. Schizophren sind dabei die Lorentz-Transformationen, die meine Behauptung zwar bestätigen, aber nicht wirklich verstanden werden, weil man sich alles doch nur dreidimensional vorstellt und sich dementsprechend für richtig oder falsch entscheidet.

Denn eine Lorentz-Transformation beschreibt nämlich auch die Spiegelung bzw. die Inversion aller räumlichen Koordinaten. Womit eine 5. oder „Nullte“ Dimension dann die Zeit darstellt, die für den Fortschritt oder letztendlich für die Krümmung sorgt. Und bei der Inversion widerspricht die Zeit ihrer unidirektionalen Sonderrolle. 

Jede Krümmung endet als Kreis, und damit folgt sie auch dem Verhältnis zweier senkrecht zueinander stehenden Dimensionen, und jenes Verhältnis folgt der einer trigonometrischen Gesetzmäßigkeit, die uns z.B. als Sinusfunktion bekannt ist, welche sowohl positive als auch negative Resultate produziert, und somit wird wiederum einer möglichen unidirektionalen Sonderstellung widersprochen.

Ein plausibles 4D Koordinatensystem benötigt daher ausnahmslos vier bidirektional quantitative Dimensionen, die alle gleichberechtigt sind und keiner Hierarchie folgen. Denn aus jeder beliebigen Perspektive heraus muss eine relative Position bestimmt werden können, ohne dass präpositionale Adverbien wie z.B. links oder rechts usw. notwendig wären, denn jene Merkmale sind die bekannten Relativitäten, die sich mathematisch als das Signum der Quantität darstellen, also die mathematischen Vorzeichen der Koordinaten darstellen. Und zwar vom Nullpunkt oder Bezugspunkt des Betrachters aus.

Denn wie ich bereits unter der vorherigen Frage beschrieben habe, addieren sich nur die räumlich gegenwärtige Intensität der Wirkungen, aber aus jeder beliebigen Richtung heraus, und zwar auch aus der Richtung, die sich als Zeit verstanden wissen will, aber wegen ihrer Sonderstellung mathematisch überhaupt keinen räumlichen Bezug hat. Denn die Konsequenz der Relativitätstheorie bedeutet, dass eine allgemeine Aussage über eine Wirkung unmöglich ist, die an jedem anderen Ort des Universums gültig wäre.

Eine Sonderstellung aber kennzeichnet ein 4D-Koordinatensystem und somit verliert es seine universelle Möglichkeit, aus jeder erdenklichen 4D-Perspektive heraus eine identische Aussage über die Relativität zu treffen.

Auch ist die Krümmung der Zeit sowieso nur eine verbale Verballhornung des Begriffs „Zeit-Dauer“, die von rein räumlicher Natur ist, denn sie folgt widerspruchslos den bidirektional quantitativen trigonometrischen Konsequenzen einer Krümmung. Somit bestimmen mindestens fünf Dimensionen das Geschehen, und die 5. Dimension, die wir als Zeit begreifen, ist dann die eigentliche Ursache der Veränderungen im 4D-System. Und solch eine Krümmung beschreibt sich dann wie folgt:

Stellen wir uns vor, dass jede Dimension gleichzeitig einen Planckschen Schritt vorwärts zählt, dann endet jede Krümmung letztendlich als Kreis. Doch endet er nur scheinbar am gleichen Punkt, also nicht am Selben, sondern auch die 4. Koordinate erfährt diese Veränderung. Und wer es nicht gelernt hat, so etwas richtig zu deuten, der fällt auf Schrödingers paradoxe Katzenfalle rein. Denn das Objekt der Betrachtung bewegt sich nicht durch den Raum, sondern es ändert sich nur die äußere Perspektive bzw. die Zeit, deren äußerste räumliche Position eines 5D-Systems den relativistischen Bezugspunkt bestimmt.

Es ändert sich also nicht die ursächlich reale Quelle der Wirkungen im 4D-System, sondern nur die äußerste Perspektive. Womit im Inneren des 4D-Systems nicht das kleinste Fünkchen Energie verbraucht wird, um den aktuellen Überlagerungszustand zu verändern, in dem sich völlig neue Konstellationen der Überlagerungen bilden, die wiederum an jedem Punkt des Universums die Intensität der Wirkung ändern. Und weil wir davon nur der maximalen Amplitude der Intensität folgen, glauben wir, dass sich die Dinge real bewegen.

Somit stellt sich nun die folgende Frage:

Wie sollte ich mir eine Lorentz-Transformation räumlich vorstellen und was fange ich damit an, wenn ich doch die Vorstellung von absoluter Zeit aufgeben muss?

Mir erscheint es viel wahrscheinlicher, dass es sich bei der Längenkontraktion um die Ursache handelt, anstatt um die Wirkung, da die zeitliche Ursache dagegen eine deutlich geringere Wahrscheinlichkeit bietet. Mir stellt sich vor allem die Frage, warum die Zeit als Ursache gewählt wurde. Gibt es möglicherweise Gründe dafür?

Der Vorteil meiner Überlegung wäre nämlich, dass ein räumlicher Abstand bereits die notwendigen Eigenschaften hat, um mathematisch plausibel zu sein, und keinerlei hypothetischer Konstruktionen notwendig sind oder prinzipielle Bedingungen erfüllt werden müssen, die eine gleichzeitig beliebig genaue Bestimmung von Ort und Impuls verbieten und damit der Mathematik nur unbestimmt wahrscheinliche Lösungswege aufzwingt. Obwohl die Längenkontraktion völlig unkomplizierte Vorhersagen von Ort und Impuls auch im ruhenden Zustand ermöglicht.

Denn inzwischen häufen sich nämlich die akademisch korrekt belegbaren Feststellungen, dass die notwendige 4. Dimension nur von räumlicher Natur sein kann. Siehe dazu z.B. die Antwort auf die Frage von CatsEyes.
Was ist "Photon-Photon-Streuung"?

Ich hatte zwar bereits die folgenden Fragen gestellt:

Ist Zeit eine Qualität und von unidirektional invarianter Natur,
oder ist sie eine Quantität von bidirektional variierender Natur?

Wie kommt die Zeit zu ihrer Quantität, um sie als Formel nutzen zu können?

Dennoch erhielt ich bisher noch keine befriedigende Antwort, und auch wenn teilweise konstruktive Diskussionen entstanden sind, könnte ich nicht von einer befriedigende Antwort sprechen.

Betrifft die Relativität:
Ausgehend von zwei vorangehenden Fragen, die mit der folgenden Frage begannen:

Warum wird angenommen,
dass eine Längenkontraktion durch die Zeitdilatation verursacht wird,
wenn es auch umgekehrt erklärbar wäre?

... musste ich dort eine weitere Frage stellen.

Welcher Prozess verursacht die Veränderung des räumlichen Zustands, was wir letztendlich als Dehnung der Zeit oder Kontraktion des Raums verstehen könnten?

… womit ich nun hier bei dieser Frage ankam, weil komplexe physikalische Zusammenhänge nun mal deutlich mehr als 5000 Buchstaben verbrauchen, als ein gewöhnlicher Troll einen verbalen Furz mit wenigen Buchstaben hier von sich gibt.

Denn die Relativitätstheorie ist kein leichtes Thema, weil die meisten Antworten einen zeitlichen Zusammenhang suggerieren, den es real gar nicht gibt. Es ist nämlich so, dass der Begriff „Zeit“ wissenschaftlich unscharf ist und uns daher nicht mehr zwischen dem Begriff „Zeit-Punkt“ und „Zeit-Dauer“ unterscheiden lässt.

Auf diese Weise wird jede zeitlich ausgerichtete Antwort zur unnötigen Bremse des Verstands, denn der Weg über die Zeit weist unseren Verstand in eine Richtung, die in einer Sackgasse endet. Weil die Zeit für die Relativität überhaupt nicht relevant ist, sondern ausschließlich eine 4. räumliche Dimension, die die bidirektionale quantitative Plausibilität wiederherstellt.

Darum ist es nun nötig zu erklären, warum die Relativität keinen zeitlichen Bezug haben kann, denn es gibt eine simple Ursache, die dafür verantwortlich ist, dass an jedem Punkt des Universums eine eigene individuelle Intensität der gravitativen Wirkung präsent ist. Genau daher ist es nicht möglich, eine allgemeine Aussage über eine Wirkung zu machen, die an jedem anderen Ort der Welt gültig wäre.

Grund dafür ist unsere optische Wahrnehmung, die nicht nur Ähnlichkeiten mit einer Wirkung aufweist, sondern identisch ist. Daher beginne ich gleich hier im Kommentar zur Frage schon mit der Antwort, damit man entsprechend antworten kann. Also:

Das Problem einer Betrachtung ist, dass wir bei unseren optischen Beobachtungen nicht die natürliche Filterung der optischen Wahrnehmung berücksichtigen. Denn wir betrachten alles immer nur aus einer inneren Sphäre heraus, wobei wir immer das Zentrum der Betrachtung darstellen. Du kannst dir aber sicher sein, dass du an jeder beliebigen Position im Universum das gleiche Phänomen erlebst. Denn die natürliche Filterung der optischen Wahrnehmung findet an jenem Ort die gleichen Bedingungen vor, weil du das Filter mit dir herumschleppst.

Es sind nämlich deine Augen. Jene Wahrnehmung wirkt konkret wie ein Polarisationsfilter. Denn die Photonen bewegen sich in alle willkürlich chaotischen Richtungen durch unsere Umgebung, aber es kommen nur Photonen bei uns an, deren Endziel unsere Augen sind, denn die anderen Photonen gehen ja dran vorbei.

Auf diese Weise kommen nur Photonen bei uns an, deren 0-Phasen genau in Bewegungsrichtung ausgerichtet sind. Erst im Auge oder im Messgerät vermischen sich die konkreten Impulse der Photonen zu dem, was wir als Licht bezeichnen. Denn ein Photon schwingt nicht, sondern offenbart uns lediglich seine innere Beschaffenheit, die vom Quadrat der Entfernung bestimmt wird und uns zeitlich aufgereiht als Impuls erscheint. Wobei sich seriell betrachtet dann ein kontinuierlich schwingendes Signal darstellt, weil sich eine Summe aller sich überlagernden Impulse bildet, die aus allen möglichen Richtungen am gleichen Ort superpositionieren.

• Und genau an diesem Punkt wird ersichtlich, dass der Zeit eine wirkende Quantität fehlt, denn jener Aufenthaltsort der räumlichen Addition (Überlagerung) ist ein Punkt, der sich zwischen zwei beliebigen gleichzeitig gegenwärtigen Punkten befindet, zwischen denen sich eine quantitative Wirkung bilden kann. Wogegen jene Position nur einen dimensionslosen unidirektionalen Zeit-Punkt hat, der keinesfalls eine Wirkung auf die Addition haben kann, die eine Längenkontraktion oder Zeitdilatation zufolge haben könnte.

Und dieser besagte Punkt ist physikalisch identisch mit dem Punkt im Auge. Daher erfährt jeder beliebige Punkt im Universum die gleich Addition von Wirkung, denn entlang jeder perspektivischen Line, die an einem beliebigen Punkt im All endet, mischen sich die Wirkungen zu einer Summe, die sich wegen ihrer einzigartigen Relativität von jeder anderen Position im Raum unterscheiden.

Relativität ist nämlich das: Wenn du meinst, dass dein Nachbar rechts neben dir steht, dann wähnt dein Nachbar dich links neben sich. Keiner von beiden kann eine identische Relativität besitzen. Es bilden sich also ganz eigene Intensitäten mit ganz eigenen mathematischen Vorzeichen, die als quadratische Summe einer überlagerten Wirkung eine Längenkontraktion verursachen.

Und jene Längenkontraktion ist lediglich eine Verschiebung der Mengen durch Krümmung in eine 4. räumliche Dimension.

So denke ich jetzt, du kannst etwas Konstruktives dazu sagen, was an dieser Vorstellung falsch wäre.

In meiner vorherigen Frage:

Warum wird angenommen,
dass eine Längenkontraktion durch die Zeitdilatation verursacht wird,
wenn es auch umgekehrt erklärbar wäre?

ergab sich diese Frage hier. Und somit solltest Du darauf antworten können, was mit dieser Frage eigentlich gemeint ist. Denn letztendlich ist keine Wirkung ohne Ursache, weil die Veränderung, welche das Gegenwärtige zu Vergangenem macht und damit etwas Neues entstehen lässt, immer noch die Ursache für die räumliche Veränderung, die wir als Längenkontraktion bezeichnen und wir unbedingt auch als Zeitdilatation verstehen wollen, damit die ach so geliebte Relativitätstheorie keinen Schaden nimmt. 

Es geht hier also immer noch darum, warum die 4. Dimension unbedingt von zeitlicher Natur sein muss, wenn doch die Relativität selbst nur eine beliebige Quantität benötigt, um weiterhin ihre Gültigkeit zu behalten. Es wäre auch viel plausibler, eine räumliche Dimension anzunehmen, denn der Vorteil davon wäre nämlich, dass ein räumlicher Abstand bereits die notwendigen Eigenschaften hat, um mathematisch plausibel zu sein, und keinerlei hypothetischer Konstruktionen notwendig sind oder prinzipielle Bedingungen erfüllt werden müssen, die eine gleichzeitig beliebig genaue Bestimmung von Ort und Impuls verbieten und damit der Mathematik nur unbestimmt wahrscheinliche Lösungswege aufzwingt. Obwohl die Längenkontraktion völlig unkomplizierte Vorhersagen von Ort und Impuls auch im ruhenden Zustand ermöglicht.

Denn inzwischen häufen sich nämlich die akademisch korrekt belegbaren Feststellungen, dass die notwendige 4. Dimension nur von räumlicher Natur sein kann. Siehe dazu z.B. die Antwort auf die Frage von CatsEyes.

Was ist "Photon-Photon-Streuung"?

Aber auch hierbei gilt:
Für die Relativitätstheorie wäre es nicht relevant, ob die zusätzlich benötigte Dimension von räumlicher oder zeitlicher Natur ist, denn es wird nur eine zusätzliche bidirektionale Quantität benötigt, um ihre Gültigkeit zu untermauern.

Es ist nur die Frage zu lösen:Ist Zeit eine Qualität und von unidirektional invarianter Natur,
oder ist sie eine Quantität von bidirektional variierender Natur?

Es gilt daher das Problem zu lösen, welcher Prozess die Veränderung des räumlichen Zustands verursacht, was wir letztendlich als Dehnung der Zeit oder Kontraktion des Raums verstehen könnten, damit wir endlich einsehen, dass man Zeit weder krümmen noch dehnen oder einrollen kann.

Ich möchte gerne wissen, was Du davon hältst, dass Zeit dehnbar sei (Zeitdilatation), obwohl sich doch nur reale, räumlich substanziell gegenwärtige Dinge verändern können. Denn es scheint mir offenbar so, dass Zeit nur in unserem Gedächtnis existiert, um damit rechnen zu können, und somit außerhalb des Kopfes gar nicht direkt wirken kann, weil Zeit eine rein gedankliche Hilfsgröße ist, die sich uns nur als Kette von Änderungen darstellt. Denn ich vermute mal stark, dass unser Universum kein Gedächtnis in unserem Sinne besitzt, mit dem es die physikalischen Wirkungen errechnet.

Wie erklärt das raumzeitliche Vorstellungsmodell die tatsächlichen physikalischen feststellbaren Differenzen, die real wahrgenommen werden? Ich empfinde die Hypothese von der Raumzeit für recht widersprüchlich und meine damit im Besonderen die Idee der Zeitdilatation, weil die Zeit nur in unserem Gedächtnis steckt. Also dass die Zeit einfach nur eine ausgedachte Hilfsvorstellung ist, die uns die vergangenen Wirkungen plausibel erklären soll.

Das Problem ist nämlich, dass man „Zeit“ nicht als mathematische Variable einsetzen kann, weil sie zum Einen keine Quantität ist und zum Anderen nicht bidirektional sein darf. Aus einer anderen Perspektive heraus kann sich ganz sicher keine Quantität bilden bzw. kein zeitlicher Abstand, weil ein Punkt nicht mehr gegenwärtig ist, denn bekanntlich kann nur etwas wirken, wenn die Punkte auch gegenwärtig sind.

Also, hast du eine Idee, wie man die Widersprüche plausibilisieren kann?

Mein Physiklehrer hat gesagt das wenn man in einem Auto sitzt die Zeit gleich schnell vergeht, wie wenn man nicht fährt.

Aber es ist doch so dass die Zeit dann schneller vergeht, selbst wenn es nur 0,000000000000000000001 Nanosekunden sind, der Unterschied ist ja trotzdem da oder nicht?

Lichtgeschwindigkeit ist die höchste Geschwindigkeit und nichts mit Masse kann sie erreichen.

Aber warum ist das so? Warum genau gibt es nichts was schneller als das Licht werden kann?

Warum ist die Lichtgeschwindigkeit eine Art Barriere?

Hallo,

im Rahmen meines Physik-Lk beschäftige ich mich aktuell mit der Zeitdilatation. Soweit ich das verstehe, vergeht die Zeit einer Lichtuhr in einem sehr schnell bewegten Bezugssystem für außenstehende beobachter langsamer als im Bezugssystem der Beobachter, weil das licht ja einen Längeren Weg zurücklegt und die Lichtgeschwindigkeit konstant ist. Wie würde sich das theoretisch denn mit einer Quarzuhr oder einer Meschanischen Uhr verhalten, denn diese sind ja in ihrer Funktionsweise nicht von der Lichtgeschwindigkeit abhängig?

Danke schonmal für die Antwort

Vorallem weil die Relativitätstheorie schon rein logisch unsinnig ist. Nur weil ich vielleicht schnell reise, hört mein Körper nicht auf zu altern und ich lebe nicht plötzlich 300 Jahre länger als meine Schwester.

Man kann sich nun vorstellen, dass von einem Zwillingspaar der eine im Raumschiff durchs Weltall fliegt während der andere auf der Erde bleibt. Beide sind 20 Jahre, als der eine Zwilling die Erde verlässt. Als er nach 20 Jahren seiner Zeitrechnung zurückkommt, ist er 40 Jahre, sein Bruder jedoch bereits 90 Jahre nach der Zeitrechnung auf der Erde. Man nennt dieses Phänomen das "Zwillingsparadoxon".

Meine Frage: Hat nun der 40jährige auch die körperlichen Altersprobleme wie sein 90jähriger Bruder?

Das universeIIe Zeitsynchronisationsprinzip:

1.) Zwischen 2 0bjekten gibt es immer den '0rt' der Zeitsynchronisation.

1/2×Bewegung 0bjekt 1 + 1/2×Bewegung 0bjekt 2 = Zeitsynchronisationsort.

2.) 2 Zeitsynchronisationsorte besitzen ebenfaIIs ihren eigen Zeitsynchronisationsort nach Punkt 1.)

3.) Zeitsynchronisationsorte haIbieren die AnzahI der 0bjekte im Universum und dies Iässt sich so Iange wiederholen, bis nur noch 2 0bjekte mit ihrem Zeitsynchronisationsort übrig bIeiben.

Dieser letzte 0rt ist der Takt-/Zeitgeber für aIIe 0bjekte im Universum.

Ich hab da mal irgendwas davon gehört oder täusche ich mich und das würde rein Theoretisch nicht gehen?

Die Zeit ist ein rätselhaftes Phänomen, das sich wie ein roter Faden durch die verschiedenen Wissensgebiete zieht. Welche Rolle spielt sie jeweils in Physik, Philosophie, Psychologie und Ökonomie? Und was können wir selbst dagegen tun, dass sie Zeit zu schnell vergeht?

Meine Antwortversuche dazu findet ihr hier:

was-ist-zeit-vier-verschiedene-antworten-aus-physik-philosophie-psychologie-und-ökonomie

Das Kettensägen-Paradoxon
Aus der Sicht eines ruhenden Beobachters verkürzen sich bewegte Objekte aufgrund der Längenkontraktion der speziellen Relativitätstheorie. Bei einer Kettensäge haben wir zwei Systeme. Das Schwert befindet sich im Ruhesystem und die Kette in einem gleichmäßig geradlinig bewegten System, zwischen denen man laut Relativitätsprinzip nicht unterscheiden kann.

   Wie verhält sich das jeweilige Objekt im eigenen System und wie verhält sich das jeweilige Objekt im System des anderen Objektes? Reißt die Kette oder hängt sie durch? Was ist real? Theorien gibt es viele, es gibt jedoch nur eine Realität!
.
https://paradoxon.online
.

Heyy,

ich hab zwei Physikaufgaben, die ich nicht verstehe, könnt Ihr mir helfen?

Schon mal vielen Dank!

Könnte mir bitte jemand helfen? Was habt ihr bei den beiden Aufgaben raus?

Bei 1) muss man doch die Formel der Zeitdilation nach t0 umstellen oder?

1)

Ein Beobachter auf der Erde sieht ein Raumschiff mit einer Geschwindigkeit von 0,9 c vorbeifliegen. Ermitteln Sie, wie viel Zeit für einen Beobachter auf der Erde vergeht, wenn die Bordzeit 10 y beträgt. Geben Sie die Gleichung t0 = ... an, die Sie verwendet haben.

2) Ein Satellit umkreist die Erde mit einer Geschwindigkeit von 0,99 c. Berechnen Sie, wie viel Zeit für den Satelliten vergeht, wenn auf der Erde 10 y vergehen. Geben Sie die Gleichung t = ... an, die Sie verwendet haben.

Ich habe diese Formel verwendet: 

Ich wäre dankbar, wenn ihr eine Lösung hättet, das würde mir sehr weiterhelfen.

Könnte mir bitte jemand helfen? Was habt ihr bei den beiden Aufgaben raus?

1) Ein Zug fährt mit einer Geschwindigkeit von 0,85 c relativ zur Erde. Ein Beobachter

im Zug misst die Länge eines Tunnels als 200 m. Bestimmen Sie die Länge des

Tunnels für einen Beobachter auf der Erde. Geben Sie die Gleichung l = ... an, die

Sie verwendet haben.

2) Ein Raumschiff fliegt mit einer Geschwindigkeit von 0,6 c relativ zur Erde. An Bord befindet sich ein ursprünglich 100 m langer Stab. Berechnen Sie die Länge des Stabes aus Sicht eines Beobachters auf der Erde. Geben Sie die Gleichung l0 = ... an, die Sie verwendet haben

Für die beiden Aufgaben habe ich schon die Formeln gefunden, aber ich bin mir nicht sicher, ob ich bei der Aufgabe noch die Geschwindigkeit von c (Lichtgeschwindigkeit von 300 000 km/s) brauche?

Ich wäre dankbar, wenn ihr eine Lösung hättet, das würde mir sehr weiterhelfen.

Könnte mir bitte jemand helfen? Was habt ihr bei den beiden Aufgaben raus?

1) Ein Beobachter auf der Erde sieht ein Raumschiff mit einer Geschwindigkeit

von 0,9 c vorbeifliegen. Ermitteln Sie, wie viel Zeit für einen Beobachter auf der Erde vergeht, wenn die Bordzeit 10 y beträgt. Geben Sie die Gleichung t0 = ... an, die Sie verwendet haben.

2) Ein Satellit umkreist die Erde mit einer Geschwindigkeit von 0,99 c. Berechnen Sie, wie viel Zeit für den Satelliten vergeht, wenn auf der Erde 10 y vergehen. Geben Sie die Gleichung t = ... an, die Sie verwendet haben.

Für die beiden Aufgaben habe ich schon die Formeln gefunden, aber ich bin mir nicht sicher, was ich mit den 10y machen soll. Kann ich das einfach so in die Formel einsetzen oder soll ich die 10 Jahre in Sekunden umrechnen? Bei der Geschwindigkeit, brauche ich auch noch c (Lichtgeschwindigkeit von 300 000 km/s) oder brauche ich das nicht bei der Formel?
Ich wäre dankbar, wenn ihr eine Lösung hättet, das würde mir sehr weiterhelfen.

wenn die jahre mit dem älterwerden schneller vergehen zeit wie im flug vergeht

wenn man gar niczts mehr macht und sich beginnt zu langweilen kann man es dann zumindest aufhalten? fühlt sich dann ja langsamer an

oder wenn man ganz viel erlebt und ganz viel macht dann geht es schneller rum ist das so oder

und im nachhinein fragt man sich wie man das alles in der kurzen zeit erleben konnte

Mit welcher Formel soll ich diese beiden Aufgaben zur Zeitdilatation berechnen?
Das y bei den 10y steht doch für die Jahre oder? Wie soll ich dann damit rechnen?

1) Aufgabe: Ein Beobachter auf der Erde sieht ein Raumschiff mit einer Geschwindigkeit von 0,9 c vorbeifliegen. Ermitteln Sie, wie viel Zeit für einen Beobachter auf der Erde vergeht, wenn die Bordzeit 10 y beträgt.

2) Aufgabe: Ein Satellit umkreist die Erde mit einer Geschwindigkeit von 0,99 c. Berechnen Sie, wie viel Zeit für den Satelliten vergeht, wenn auf der Erde 10 y vergehen.

Ich habe mich in letzter Zeit viel mit der Relativitätstheorie (insbesondere die allgemeine Relativitätstheorie) beschäftigt und frage mich, ob ich das Konzept der Zeitdilatation richtig verstanden habe.

Nehmen wir an, jemand reist in einem Raumschiff, das sich mit 90% der Lichtgeschwindigkeit bewegt, für ein Jahr (nach der Zeitmessung im Raumschiff).

Würde das bedeuten, dass auf der Erde weniger als ein Jahr vergangen ist, weil die Zeit im Raumschiff langsamer läuft? Oder habe ich da einen Denkfehler?

Vielen Dank :)

Könntet ihr mir bei diesen Aufgaben bitte helfen?

1) Ein Satellit umkreist die Erde mit einer Geschwindigkeit von 0,99 c. Berechnen Sie, wie viel Zeit für den Satelliten vergeht, wenn auf der Erde 10 y vergehen. Geben Sie die Gleichung t = ... an, die Sie verwendet haben.

2) Ein Beobachter auf der Erde sieht ein Raumschiff mit einer Geschwindigkeit von 0,9 c vorbeifliegen. Ermitteln Sie, wie viel Zeit für einen Beobachter auf der Erde vergeht, wenn die Bordzeit 10 y beträgt. Geben Sie die Gleichung t0 = ... an, die Sie verwendet haben.

Dankeschön.

Im Voraus: Ich bin in keinerlei hinsicht ein Physiker und mein komplettes Bild des Universums könnte fundamental falsch sein. Ich erkläre kurz, wie ich mir das vorstelle und würde dann im Nachhinein wissen, wie realistisch mein Bild ist.

Also, so wie ich mir das Universum vorstelle, leben wir in einer Welt, die mindestens 4 Dimensionen umfasst. Ich vermute mal, dass "Zeit" etwas anders funktioniert, als die anderen Dimensionen, die wir wahrnehmen. In meinem Bild ist Zeit jedoch sehr ähnlich zum Raum.

Statt einer Maximalgeschwindigkeit, stelle ich mir eine konstante Geschwindigkeit vor, in welcher wir uns durch die Raumzeit bewegen. Je schneller wir durch eine Dimension fliegen, desto langsamer tun wir das durch die anderen.

Wenn wir langsamer im Raum werden, nehmen wir an Geschwindigkeit durch die Zeit zu, so dass wir am Ende die gleiche Geschwindigkeit haben. Da wir die Zeit jedoch nicht so wahrnehmen wir den Raum, fühlen wir uns insgesamt langsamer im vergleich zu anderen Objekten, die langsamer durch die Zeit gehen, aber dafür schneller durch den Raum. Am Ende ist aber alles theoretisch "gleich schnell".

So erkläre ich mir bisher, dass wir nicht schneller als das Licht sein können. Licht bewegt sich zwar in der gleichen Geschwindigkeit wie wir, jedoch bewegt es sich ausschließlich durch Raum und nicht gleichzeitig durch Zeit.

Wie realistisch klingt dieses Bild?

ich habe es so verstanden, dass in der Nähe von Masse die Zeit langsamer vergeht. Allerdings vergeht die Zeit auch langsamer, wenn man sich schnell bewegt. Wenn ich jetzt weit weg von der Erde bin, wo also keine Gravitation auf mich wirkt, müsste die Zeit eigentlich schneller vergehen, da ich aber extrem schnell mit meiner Rakete Flieger vergeht die Zeit ja langsamer. Kann mir das jemand erklären?

Es wird ja immer gesagt, dass Zeit relativ ist, denn Zeit bildet mit dem Raum ja die Dimension Raumzeit.

Wenn sich massereiche Objekte irgendwo befinden, wird der Raum ja gekrümmt und die Zeit vergeht doch normal, aber auch Sicht eines Dritten extrem langsam. Oder man ist paar Tage neben einem schwarzen Loch und auf der Erde vergehen Jahre.

Jetzt ist meine Frage, ob es denn trotzdem eine generelle Zeit gibt? Wieso ich das frage? Naja, zwar vergehen auf der Erde Jahre und für einen selber nur wenige Tage, aber man altert trotzdem noch? Trotzdem hat man beispielsweise nur 100 Jahre zum Leben wie eine Art innere Uhr? Ist das nicht die generelle Zeit?

Frage klärt.

Hallo,

ich beschäftige mich grade privat mit dem Thema Relativitätstheorie und hätte dazu eine Frage. Und zwar ist es ja so dass wenn man sich schnell bewegt die Masse zunimmt (erst bei sehr hohen Geschwindigkeiten spürbar), dadurch die Raumzeit gekrümmt wird und somit die Zeit langsamer vergeht. So habe ich das aufheben Fall verstanden, ob das 100% richtig ist bin ich mir nicht sicher. Ich habe mir dann vorgestellt das ein Raumschiff mit sehr hoher Geschwindigkeit von Punkt A zu B fliegt, für diese Strecke braucht das Raumschiff 1 Jahr. Auf der Erde vergehen in dieser Zeit aber z.B. 5 Jahre. Ich habe mir jetzt vorgestellt das Beobachter von der Erde das Raumschiff betrachten, es sieht wie in Slowmotion aus denn es braucht aus der sich ja 5 Jahre. Nur wo ich mir jetzt unsicher bin: Wenn man jetzt annimmt das diese Raumschiff direkt an der Erdeoberfläche vorbeiflieg. Sieht es dann für die Menschen auf der Erde so aus als würde es ganz langsam vorbei fliegen was irgendwie kein Sinn ergibt. Oder ist es so das es selber die Raumzeit so stark krümmt das die Zeit um ihn rum langsamer vergeht also auch für die Beobachter an denen es vorbei fliegt. Aber das würde dann doch auch bedeuten das dieses Raumschiff eine viel stärkerer Gravitation als die Erde hätte und alles an sich zeigen würde.

Natürlich sind das alles Realitätsferne Gedankenspiele aber würde mich riesig über eine Antwort freuen um die Zeitdilatation besser zu verstehen.

Lg und danke für das durchlesen und Antworten :))

Könnte mir jemand erklären wie ich die Lorentzkontraktion und die Zeitdilatation der Relativitätstheorie, im Minkowski Diagramm geometrisch deuten kann ? Ich blicke leider beim Minkowski Diagramm noch nicht ganz durch.

Vielen Dank im Voraus (:

Früher galten viele Dinge auch als unmöglich, aber sind heute möglich. Ein anderes Problem wäre jedoch, falls wir es schaffen würden mit Lichtgeschwindigkeit zu reisen, würde es uns nicht viel bringen, weil das Universum so groß ist, selbst der nächste Stern würde lange dauern, selbst mit Lichtgeschwindigkeit.

Aber habt ihr Ideen wie wir diese Geschwindigkeit erreichen könnten?

wieso altere ich schneller desto schneller ich mich bewege? wieso idt das weltall wie eine zeitreise? idt zeit überhaupt echt? wozu gibt es überhaupt zeit? ist zeit die 4. dimension?

Hallo zusammen ich beschäftige mich gerade mit der speziellen Relativitätstheorie und verstehe das mit dem ZwillingParadoxon als Folge der Zeitdilatation nicht so ganz.Könnte mir das eventuell jemand möglichst einfach erklären

Hallo zusammen, ich halte eine Physik Gfs über das Thema spezielle Relativitätstheorie und habe einige fragen…

Warum ist wie oben gestellt das langsamere altern möglich dies würde doch bedeuten das man theoretisch in einem Raumschiff bei Lichtgeschwindigkeit reißen kann wenn das möglich wäre und beim auf die Erde zurückkommen die gleichaltrigen viel älter sind oder nicht mehr leben.Wie ist das möglich warum altern die menschlichen Zellen langsamer und würde dies bedeuten wenn man theoretisch schneller als Lichtgeschwindigkeit unterwegs wäre könnte man Zeitreisen?

Warum kann man sich nicht schneller als Lichtgeschwindigkeit bewegen?Wenn zwei Züge mit Lichtgeschwindigkeit aufeinander zu fahren.Warum treffen sie sich dann nicht schneller als wenn einer mit Lichtgeschwindigkeit fährt und der andere steht.

Stimmt es das man Laut der speziellen Relativitätstheorie langsamer altert aufgrund der Zeitdilatation.Warum altert man nicht gleich schnell die menschlichen Zellen altern doch immer gleich warum wird dies beeinflusst wenn sich das Intertialsystem schneller bzw. relativ schneller zb Mensch im Raumschiff zu Mensch auf Erde.

Hallo zusammen

Wenn man sich mit einer hohen Geschwindigkeit, nahe der Lichtgeschwindigkeit bewegt, vergeht für denjenigen im bewegten System die Zeit ja viel langsamer als für einen Beobachter in einem unbewegten System.

Wenn das Raumschiff mit 99.99% der Lichtgeschwindigkeit zu einem 1000 Lichtjahre entfernten Stern fliegt, würde es ja von der Erde so aussehen, als würde das Raumschiff mehr als 1000 Jahre brauchen. Für die Besatzung des Raumschiffs aber vergeht die Zeit viel viel schneller und eventuell brauchen sie nur einige Wochen oder Monate für die Strecke.

Nehmen wir jetzt mal an, das Raumschiff würde sich mit Lichtgeschwindigkeit bewegen (ja ich weis ist nicht möglich, aber es geht dabei nur um ein Gefankenexperiment)

Jedenfalls würde ja für die Besatzung des Raumschiffs bei Lichtgeschwindigkeit die Zeit quasi still stehen. Wenn sie jetzt eine Reise zu einem Stern, der einige 1000 Lichtjahre entfernt liegt unternehmen würden, gehe ich dann richtig in der Annahme, das es für die Besatzung so wäre, dass sie sofort ankommen und falls sie nicht bremsen würden und sich weiter mit Lichtgeschwindigkeit fortbewegen würden quasi sofort ans Ende des Universums kommen würden?

Was genau verursacht diesen Effekt, ist es so, dass die Raumzeit bei derart hoher Geschwindigkeit so massiv gekrümmt wird, das quasi keine Distanz mehr zwischen den beiden Punkten liegt?

Danke für euere Hilfe

Die Frage ging mir durch den Kopf wegen einer andern Frage zum Thema Licht heute morgen: Angenommen ein Raumschiff fliegt mit 99,999 % Lichtgeschwindigkeit - und sendet einen Laserstrahl aus: Kriecht der im Schneckentempo vom Schiff weg? Oder saust er mit Tempo "c" davon? Und wäre das dann nicht doppelte Lichtgeschwindigkeit?

Laut der Relativitätstheorie würde ein extrem schnelles Raumschiff in Zeitlupe als aussenstehender auf der Erde fliegen. Dann wäre es doch abgesehenden von den Reisenden praktisch für die Menschheit nicht wirklich möglich, unser Sonnensystem zu verlassen (bemannt)

Oder?

https://youtu.be/QuSPOud3s5s?si=gCUomDBvL31BtC-C

In der oben angeben YouTube Doku über die Relativitätstheorie von Albert Einstein ist mir aufgefallen, dass ich laut der Theorie in die Zukunft lande wenn ich mit Lichtgeschwindigkeit reise. Aber gleichzeitig ein relativ zu mir befindendes Objekt langsamer wahrnehme. Das sieht für mich wie ein Widerspruch aus. Denn wie kann es sein, dass ich 1000 Jahre in die Zukunft reise während ich gleichzeitig einen Vorgang der vielleicht normalerweise 10 Minuten dauert mir so vorkommt als wären es mehrere Stunden. Aber das scheint wohl so zu sein. Laut dieser Doku. Darauf habe ich hier diese Frage gestellt und bekam hochkomplizierte Antworten.

Ich wollte hier nochmal wissen was ich dann sehe wenn ich mich in Lichtgeschwindigkeit in die Zukunft bewege.

Nehmen wir an ich bin in einem Auto das fast Lichtgeschwindigkeit fährt. Ich pendle nur 1 m hin und her im Zick Zack.

Für mich geht die Zeit langsamer weil alles im Auto langsamer läuft aber draußen vergehen 1000 Jahre.

Was sehe ich nun draußen.

Theoretisch befindet sich alles Relativ zu mir. Ich müsste also alles langsamer sehen. Wie kann es dann sein das 1000 Jahre vergangen sind ?

Zudem kommt hinzu, dass ich einen Zähler im Auto habe der mitzählt wie häufig ich hin und her gependelt bin für mich muss ich eine normale Summe sehen können die entsprechend der Lichtgeschwindigkeit innerhalb von 10 Minuten entstanden ist. Jedoch müsste ich ja aufgrund der 1000 Jahre die ich in die Zukunft gereist bin ein viel viel häufiger gependelt sein, sodass der Zeiger mit überlichtgeschwindigkeit abermilliarden häufigere zyklen anzeigen.

Wie passt das am Ende Zusammen ?

Denn das Auto ist genauso schnell wie ich und das wird dann auch nur soviele Zyklen anzeigen können wie ich innerhalb von 10 Minuten zurücklegen kann

Wenn man in einem Raumschiff mit 99,9999999% Lichtgeschwindigkeit zur Andromeda Galaxie fliegen würde, würde es sich dann so anfühlen, als ob man 2,5 Millionen Jahre gereist ist jedoch nur ein bisschen wegen der Zeitdilatation gealtert ist?

Wenn ein Raumschiff mit 99,99999% Lichtgeschwindigkeit vom der Erde wegfliegen würde, würden die Insassen die Menschen auf der Erde schneller oder langsamer sehen (Zeitdilatation) und würden die Menschen auf der Erde die Insassen schneller oder langsamer sehen?

Kann mir jemand Zeitdilatation mit einem Beispiel ausführlich erklären?

Hey Leute ihr wisst ja dass das licht ungefähr 8 min. von der Sonne zur Erde braucht was ja bedeutet das Licht ist nicht direkt da und wenn man Jetzt ein Raumschiff hätte was keine Brems/Beschleunigungszeit hat und man würde direkt von der Erde mit Doppelter Lichtgeschwindigkeit starten und Kurze zeit Später wieder stoppen könnten wir selber uns dann von der Erde aus starten sehen weil uns dann ja unser licht sozusagen Hinterher kommt

Könnte jemand mir bitte helfen die Aufgabe zu lösen. Ich verstehe einfach nicht wie ich es rechnen soll. Ich weiß nur das es etwas mit dem Zwillingspardoxon zu tun hat.
Ich würde mich über eine Antwort mit Lösungen bzw. Erklärungen supper stark freuen.

Hi zusammen,

Bei Leifiphysik wird eine Gleichung umgeformt um die Formel der Zeitdilation herzuleiten. Dabei verstehe ich die letzte Umformung nicht.

https://www.leifiphysik.de/relativitaetstheorie/spezielle-relativitaetstheorie/grundwissen/zeitdilatation

Kann mir jemand erklären, wie das gemacht wird und welche Rechenregeln angewandt werden?

Hier nochmal ein Screenshot von der letzten Umformung:

Vielen Dank im Voraus!!!

Auf der erde mit Lichtgeschwindigkeit reist, hört man dann irgendwas? Denn Schall ist ja langsamer als Licht

Gemäß der Relativitätstheorie ist es so dass ich die Welt in zeitlupe sehe während wenn ich hohe geschwindigkeiten zb. 10 prozent der lichtgeschwindigkeit erreiche. Jedoch gleichzeitig soll ich doch in die Zukunft gerreist sein ?

Also muss ich ja die welt nicht in Zeitlupe sondern in alltempo sehen können ? Damit das zusammenpasst?

Andonsten bin ich irgendwie in der falschen welt gelandet. Denn wenn ich mich mit lichtgeschwindigkeit bewege dann sieht der beobachter auf der Erde dass die Uhren bei mir langsammer ticken. Jedoch sehe ich das bei ihm genauso wenn ich zu ihm schaue. Trotsdem soll ich in die Zukunft gereist sein ?

Wo bleiben dann die 100 jahre erlebnis die ich nie gesehen habe? Während ich bloß 1 minute lang im raumschiff wahr und den letzten kometenanschlag auf der Erde so wahrnahm als wenn es 10 minuten gedauert hat obwohl der beobachter auf der Erde selbst den vorgang nur in 1 minute wahrnahm ?

Wie passt das damit zusammen dass nach der 1 minute aufeinmal 100 jahre um sind wenn ich dann zurück auf die Erde lande?

Ich kann mich nicht mehr daran erinnern wann ich das gehört hab aber desto schneller man ist desto langsamer vergeht doch Zeit oder? Und wenn man in Lichtgeschwindigkeit rennt würde die Zeit stoppen ich weiß nicht mehr von welchem YouTube Video ich das letztes Jahr gehört hab aber liegt daran was? Danke im Voraus :)

. Wie kriege ich das Gefühl dass die Zeit in der Schule schneller vergeht ?.

das heißt, postuliert die allgemeine Relativitätstheorie die Möglichkeit einer mehrfachen Lichtgeschwindigkeit?

Würde dann die Zeit langsamer vergehen und wenn ja, würde dann der Alterungsprozess bei den Lebewesen auf der Erde langsamer fortschreiten?

Wenn ich auf einem Planeten stehe und Folgendes beobachte. Ein Photon kommt auf mich zu. In der Gleichen zeit startet ein Raumschiff, dass sich auf das Photon zubewegt. Bewegen sich dann das Raumschaft und das Phonon relativ zu einander schneller als die Lichtgeschwindigkeit. Wenn nicht dann müsste ich ja als Beobachter sehen wie das Photon langsamer wird oder das Raumschiff könnte garnicht starten.

Wenn zwei Raumschiffe sich mit 50 % der Lichtgeschwindigkeit in die entgegengesetzte Richtung bewegen. Bewegen sie sich dann nicht relativ zu einander mit Lichtgeschwindigkeit?

Und was ist wenn sich ein Raumschiff in die entgegengesetzte Richtung bewegt wie ein Photon. Wenn man nicht schneller als licht sein kann dann müsste ja entweder Photon langsamer werden oder das Raumschiff sich Garnichts bewegen können.

Wer meine letzten Fragen gelesen hat, hat ja die Frage mit Lichtgeschwindigkeit und Zeit mitbekommen.

Nehmen wir an ich reise mit einer hohen Geschwindigkeiten aber langsamer als Lichtgeschwindigkeit. Die Zeit, sagen wir in Zug, verläuft langsamer als draußen. Heißt also ich kriege weniger Zeit mit als Leute draußen.

Wenn ich jetzt 3 Jahre lang fahre, kommt es mir vor wie 3 Jahre, aber außen wie 5 Jahre vielleicht.

So da noch eine Ergänzung, Photonen reisen mit Lichtgeschwindigkeit. Wie im Beispiel heißt das doch, dass bei Lichtgeschwindigkeit nahezu keine Zeit vergeht. Heißt während ich vlt 10 Sekunde Reise könnte außen 20 Jahre vergangen sein (ich weiß Grade nicht wie stark die Zeitdilatation bei Lichtgeschwindigkeit ist laut meiner Recherche vergeht garkeine Zeit)

Die Person im Zug kriegt weniger Zeit mit als außen, wenn jetzt im Zug garkeine Zeit vergeht wie meine Recherche. Heißt das nicht das nie eine Sekunde vergeht für den Reisenden. Für den Reisenden ist dann ja jede Distanz gleich lang.

Bei meiner letzten Frage meinte man für den Reisenden vergeht die Zeit normal wie außen nur man altert nicht. Aber das stimmt ja nicht, die Uhr als Beispiel bleibt ja auch stehen und alles was für den reisenden passiert muss langsamer sein als außen. Für den Reisenden fühlt es sich normal an aber die Zeit ist kürzer als außen.

hallo,

aus einsteins spezieller relativitätstheorie lässt sich ableiten, dass die betrachtungspunkte aller (theoretischen) beobachter gleichermaßen valide sind und dass infolgedessen mein "jetzt" ein anderes ist als das "jetzt" von jemand anderem.

ich verstehe das allerdings noch nicht so richtig. könnte man nicht sagen, dass "jetzt" der zeitpunkt ist, in dem die information von etwas quasi "ausgelöst", unabhängig davon wann sie mich erreicht? also wenn ich z.b. sterne beobachte, bin ich mir ja bewusst dass diese sterne nicht "jetzt" da sind, sondern dass die information einfach nur erst jetzt bei mir ankommt. Warum soll mein betrachtungspunkt dann noch valide sein?

Wie bzw kann man dir Zeitdilatation oder den Einfluss von Masse auf die Zeit eines Objektes berechnen ? Ich meine nicht die spezielle Formel t*wurzel(1-…) sondern eben für beschleunigungen/masse

Ich wollte fragen, wenn ich z.B. um 6 morgens nach Japan fliege und die Flugzeit dauert 10 Stunden, dann müsste ich um 16 dort ankommen, aber dann sehe ich, dass es 23 Uhr schon ist. Warum sind dieser 7 Stunden Unterschied? Wo sind die 7 Stunden? Hab ich an Zeit gewonnen oder wie? Ich freue mich auf hilfreiche Antworten. Danke

Lichtgeschwindigkeit sagt ja nicht nur die Geschwindigkeit von Licht aus sondern auch die Grenze die im Universum erreicht werden kann.

Das heißt doch das sich auch Zeit mit 300.000km/s durch den Raum bewegt oder?

Das heißt ja das die Zeit stillstehen würde sobald man Lichtgeschwindigkeit erreicht oder liege ich falsch?

Dazu aber 2 fragen.

1. Wenn ich mit Lichtgeschwindigkeit reise würde die Zeit für mich ja stillstehen. Wenn ich jetzt 60 Lichtjahre reise, sollte ich ja 60 Jahre gereist sein, ich bin aber keine Sekunde älter weil die Zeit stillsteht, währendessen alles andere um 60 Jahre älter ist oder? Wie merke ich aber das die 60 Jahre vorbei sind? Vergeht die Zeit für mich gefühlt gleich nur ich sehe es nicht auf einer Uhr oder bei mein körperlichen aussehen?

2. Wenn ich mit überlichtgeschwindigkeit reise (was Physikalisch unmöglich ist, aber jetzt nur so annehmen), würde die Zeit für mich rückwärts laufen?

Wenn ich darüber nachdenke ergibt es kein Sinn für mich, ich denke mehr das ich die Zeit einhole. Sozusagen ich bin in der Zukunft dann, einen Zeitpunkt den Zeit noch nicht erreicht hat. Ich bin in der Zukunft aber die Zukunft existiert ja nicht, also existiere ich nicht. Ich Verschwende dann und sobald ich bremse tauche ich wieder auf weil mich Zeit wieder einholt.

Ich bin nicht allwissend über Physik was niemand ist, aber ich weiß viel zu wenig und möchte viel mehr wissen, weswegen ich auch Physik studieren will. Wenn ich falsch liege, komplett falsch, dann korrigiert mich bitte und ergänzt Sachen damit ich mehr erfahren kann.

Danke im vorraus!

Wenn man dich sagt, dass sich alles Gleichzeitig im Raum als auch in der Zeit bewegt, und die Zeit immer langsamer wird, je mehr man sich der Lichtgeschwindigkeit nähert bis sie schlussendlich still steht, warum wird Lichtgeschwindigkeit dann nicht als unendlich anerkannt, schließlich soll man sie ja auch nicht überschreiten können.

Nach der Vorstellung, sind Prinzipien wie Distanz/Dauer (Km/h) nichtegr anwendbar, da man sich ja nur noch im Raum bewegt.

Wenn ich also von der Erde zur Sonne fliege, vergehen für den Beobachter zwar 8 Minuten, ich jedoch bewege mich nur noch im Raum, und bin somit "sofort" da - schließlich vergeht für mich keine Zeit.

Wie ist das also?

Eine Uhr bewegt sich mit v = 0,6c nacheinander an zwei ruhenden, synchronen Uhren vorbei. Als sie an der ersten Uhr vorbeifliegt, zeigt die bewegte Uhr 2 Sekunden und die ruhende Uhr 3 Sekunden. Als sie an der zweiten Uhr vorbeifliegt, zeigt diese gerade 8 Sekunden. Welche Zeit wird in diesem Moment auf der bewegten Uhr angezeigt? Meine Lösung wäre 6,4sekund stimmt es ?

Wenn ich mit Lichtgeschwindigkeit reisen würde in einem Raumschiff und ich würde mit einem Freund welcher auf der Erde ist Videochatten (angenommen das würde funktionieren), würde ich dann meinen Freund in Zeitraffer altern sehen wenn er einfach die ganze Zeit da sitzen würde? Rein Theoretisch.

Was hätte Rom gesehen wenn er auf den Planeten schaut auf dem 1Std ca. 7 Jahren auf der Erde entspricht ? Hätte er die Crew in Zeitlupe Gesehen? Gibt es für sowas eine logische/theoretische Erklärung oder sind meine Gedanken zu weit hergeholt um logisch zu sein?

Wenn man in der nähe eines Schwrzen Lochs ist ver geht die Zeit für einen Selber ja schneller als für leute auf der Erde. Würdr also ein Schwarzes Loch in der nähe der Erde auftauchen so aus dem nichts würden die Zeiger bei den Uhren anfangen sich schneller zu drehen?

Ich habe letztens den Film Interstellar - der wissenschaftlich geprüft ist - gesehen. Dort erfährt man ja, dass die Zeit schneller vergeht, wenn man an einem Ort ist, wo die Raumzeit stark gekrümmt ist. Andersrum betrachtet, je weniger die Raumzeit gekrümmt ist, desto langsamer vergeht die Zeit.

Aber unsere Erde krümmt den Raum ja auch... Zwar nicht zu vergleichen mit einem Schwarzen Loch, aber auch nicht null.

Vergeht die Zeit also langsamer als hier, wenn man sich irgendwo weiter weg befindet, wo die Raumzeit weniger gekrümmt ist? Und kann man die Zeit bei gar keiner Raumkrümmung (was ja eigentlich nicht geht, denn Gravitation wirkt von überall nach überall) als eine Art "absolute Zeit" und alles andere als eine Art "gestauchte Zeit" bezeichnen?

Ich hab letztens Interstellar gesehen, und dort vergeht die Zeit viel schneller, weil sich die Charaktere in der Nähe von einem schwarzen Loch - also in einem stark gekrümmten und sehr von Gravitation beeinflussten Raum - befinden.

Warum ist das so? Ich kenne den gleichen Effekt ja von der Zeitdilatation, also dass die Zeit langsamer vergeht, wenn man schneller ist... aber der gleiche Effekt wegen Raumkrümmung? Hat das eine mit dem anderen was zu tun? Und wenn ja, wie ist der Zusammenhang und warum gibt es diesen Effekt auch dort?

Hallo, wieso vergeht für einen Zeit langsamer, wenn man sich sehr schnell bewegt. (Nur theoretisch gesehen mit z.B 90 Prozent der Lichtgeschwindigkeit)

Ich weiß natürlich, dass es unmöglich ist, schneller als das Licht zu sein. Trotzdem will ich diese Tatsache für diese Frage ignorieren.

Wenn man sich immer schneller fortbewegt, macht man irgendwann (von außen betrachtet) die Beobachtung, dass die Zeit für die Reisenden immer langsamer vergeht, je mehr man sich der Lichtgeschwindigkeit annähert. Das ist ja die Zeitdilatation.

Könnte man mit der exakten Lichtgeschwindigkeit reisen, würde die Zeit schließlich zum Stillstand kommen und nicht mehr "weiterlaufen".

Meine Überlegung war nun, ob sich die Zeitdilatation bei Überlichtgeschwindigkeit dann einfach andersherum abspielt, also die Zeit immer schneller vergeht anstatt immer langsamer... Die Lichtgeschwindigkeit stellt da ja auch so eine Art "Grenze" dar, und dahinter würde sich das Phänomen einfach andersherum abspielen...

Vermutlich ist mein Gedankengang schwer nachzuvollziehen und dieses "Gedankenexperiment" ist physikalisch gesehen natürlich vollkommener Schwachsinn, aber macht diese Überlegung trotzdem irgendwie Sinn? Oder was denkt ihr darüber? Mache ich vielleicht auch irgendwo einen Denkfehler, der diesen Schwachsinn noch schwachsinniger macht...?🤣

Albert Einstein sagte, dass ein ,,ruhender" und ein gleichmäßig bewegter Körper nicht voneinander zu unterscheiden sind. Fährt ein Zug ab, kann man genau so gut sagen, der Zug bleibt stehen und die Erde unter dem Zug bewegt sich. Beide Aussagen sind gleich viel ,,wert".

Dann verstehe ich aber die Zeitdilatation nicht. Es gibt oft das Beispiel mit der Lichtuhr im Raumschiff. Die Lichtuhr läuft für den ruhenden Beobachter langsamer als für den gleichmäßig bewegten Raumschiff-Passagier. Ebenfalls bemerkt der Raumschiff-Passagier, dass sich die Zeit des ,,ruhenden" Beobachters schneller fortbewegt, als seine eigene. Boom, genau das ist es aber. Dann sind ja sehr wohl beide Inertialsysteme voneinander unterscheidbar. Der Raumschifffahrer weiß, dass seine Uhr schneller als die des Beobachters geht. Der Beobachter weiß, dass die Raumschiffuhr langsamer als seine Uhr geht und seine Uhr somit schneller läuft.

Wo liegt der Denkfehler?

Ich habe mich letztens sehr mit der Relativitätstheorie von Albert Einstein beschäftigt und hätte gerne eure Meinung über meine Theorie.

Albert Einstein sagte ja das Zeit relativ ist und Isaac Newton sagte das Zeit absolut ist. Es ist klar, dass viele sagen, dass Newton falsch lag, aber in meinen Augen hatten beide recht.

Isaac Newton hat uns die Grundidee der Zeit geliefert und Albert Einstein hat sie weiter ausgebaut.

Bei bestimmten Umständen kann es zur einer Zeitdilatation kommen und somit wäre die Zeit so gesehen verändert wurden.

Aber was ist mit dem Hintergrund? Also, das Gesamtbild des Universums, da vergeht die Zeit normal weiter ohne Veränderungen und sonstiges.

Es kommt ja nur zu einer Zeitdilatation wegen massereicher Objekte, oder weil sich ein Objekt mit fast Lichtgeschwindigkeit bewegt. Auch hier auf der Erde kommt es zur einer kleinen Zeitdilatation, aber für uns ja nicht wahrnehmbar.

Aber auch wenn es solche kleine Veränderungen gibt geht doch die Zeit weiter und lässt sich nicht komplett verändern, sie scheint einen bestimmten Ablauf zu haben, was nur im Vakuum wahrnehmbar ist fernab von massereichen Objekten. Sie geht da weiter, und wenn es zur eine Zeitdilatation 1.000 Lichtjahre entfernt kommt lässt sie sich nicht verändern, sie geht weiter.

Also nehmen wir an, das ganze Universum hätte eine Uhr, sie würde sich nicht verändern, wenn irgendwo eine Zeitdilatation geben sollte, sie würde ihren Ablauf beibehalten. Was wäre, wenn wir Menschen nicht die ganze Zeit wahrnehmen können, sondern nur ein Bruchstück davon, weil unser Intellekt nicht in der Lage ist es wahrnehmen zu können? Also für uns ist die Zeit relativ, auch in der näheren Umgebung, aber für das Universum bleibt sie absolut.

Bin ich damit richtig? Wie sieht ihr es?

Es gibt ja ein gedankenexperiment um die relativistische masse auszurechnen, bei dem ein auto gegen eine wand fährt. Ein schneller beobachter sieht dass geschehen, jedoch wird oft gesagt dass für den schnellen beobachter das auto langsamer ist und somit eine höhere masse hat.das macht aber für mich keinen sinn, dass das auto in seiner Perspektive langsamer ist, da bei im die uhren langsamer gehen und das auto somit für die selbe strecke weniger zeit benötigt und somit schneller ist, dann muss aber auch die masse kleiner sein , das ist ja aber falsch.

Ja, ich verstehe es: desto schneller man wird, desto langsamer verläuft die Umgebung um einen bla bla bla. Haben wir alle gelernt. ABER "Wieso?", denn ja jeder kann sich die grundlegenden Regeln hnd Erkenntnisse merken, aber das wichtigste -für mich ist immer das Warum.

Ich stelle es mir wie folgt vor:

Wenn ich in einem Auto sitze und das Auto vor mir schneller ist (Beschleunigung), entfernt es sich immer weiter. Wenn wir nun beide mit konstanter selber Geschwindigkeit fahren und die Umgebung ignorieren, sieht es so aus, als würde das Auto vor mir an einer Stelle bleiben. Wenn ich nun beschleunige, dann wird das andere immer langsamer. Ab einem bestimmten Punkt so langsam, dass ich 2000km/s zurück lege und er nur 100m/s. Für ihn ist dann eine Sekunde auf seiner Strecke verlaufen, bei mir doch aber auch? Wenn man es sich wie einen Graphen vorstellt, dann würde ich weiter in der Strecke(Raum) sein, er weniger aber auf doch auf der gleichen Zeit?

Naja, was dagegen spricht ist, dass dann die "Kästchen" bei der Raumzeit kürzer werden, da man für ein so ein Kästchen (der ja bspw. y= Raum und x= Zeit entspricht) weniger Zeit braucht, d.h. bspw. mehr Meter pro Kästchen zurücklegt.

Die zweite Überlegung war, dass ich auf gleicher Strecke schneller bin als der andere, so wäre für mich weniger Zeit vergangen für die selbe Strecke.

Und die letzte ist, dass man was ich gerade mit den Autos beschrieben habe auf das Licht übertragen kann. Wenn ich immer schneller werde und mich von etwas weg bewege, dann wird es mir langsamer erscheinen, da das Licht später ankommt (vorallem bei Geschwindigkeiten nahe Lichtgeschwindigkeit) als das Licht auf welches ich zu fahre.

Irgendwie schaffe ich es nicht alles zusammen zu puzzeln. Ich könnte jetzt wie alle anderen inklusive meiner Physiklehrer sagen, dass es eif. so ist, aber ich will es verstehen. Irgendwo fehlt ein Puzzel in meinen Überlegungen. Liegt es alleine am Licht wieso es uns die Umgebung langsamer dann vorkommt?

Hallo. Ich verstehe nicht ganz wie Gravitation die Zeit verändern kann, es ist ja nur Anziehungskraft, erklärt es mal bitte ganz einfach

Wenn der eine (unbewegte) Zwilling zB 10a lebt und der bewegte 5a, lässt sich das ja mit einer Formel mit dem Lorentzfaktor berechnen. Hier weiß der bewegte Zwilling ja dass er bewegt ist da er beschleunigt hat.

Bei der Berechnung der Eigenzeit z.B. von Myonen, die sich mit sehr hoher Geschwindigkeit nahe c, bekommt man als Betrachter der Erde ja eine deutlich höhere Zeit raus wie lange die Myonen im Inertialsystem der Erde leben, im Inertialsystem der Myonen aber ist die Lebenszeit verkürzt.

Wenn man aber im Inertialsystem der Myonen ist und die Zeit der Erde ausrechnen will, käme man ja auf eine geringere Zeit als die der Lebensdauer der Myonen. Das ist doch ein Widerspruch. Ist jetzt die Lebenszeit der Myonen auf der Erde länger oder kürzer als die Eigenzeit der Lebensdauer, die die Myonen in ihrem Inertialsystem erfahren??

Habe da wahrscheinlich einen Denkfehler oder?

Angenommen ich stehe auf der Erde in "Ruhe". Ein Raumschiff fliegt vorbei, v nahe Lichtgeschwindigkeit. Nun vergeht die Zeit, aus meiner Sicht, im Raumschiff langsamer.

Nun schaut aber der Astronaut im Raumschiff auf die Erde. Für ihn bewegt sich die Erde mit v, er ist in "Ruhe". Für ihn vergeht also die Zeit auf der Erde langsamer.

(Zeitdilatation durch Gravitation außer Acht gelassen)

Wer hat jetzt "recht"?

Wo vergeht die Zeit "wirklich" langsamer?

Oder ist dies wirklich streng vom Auge des Betrachters abhängig und welches Inertialsystem als das Ruhende betrachtet wird?

also in einer Singularität also in einem schwarzen Loch bleibt die Zeit praktisch stehen weil die Masse den Raum krümmt und die Zeit, also ein unendlicher kleiner Raum.

Bei der Erde vergeht die Zeit um 1,0000000007 Sekunden langsamer, als im All das hat ja damit zu tuen das es weniger Gravitation im All gibt als auf die Erde das besagt ja die gravitative Zeitdilatation die basiert auf die Relativitätstheorie von Albert Einstein.

Also heißt es ja wenn man zum Beispiel wie bei den Film "Interstellar" auf einen Planeten landen würde der so nah an einem massiven schwarzen Loch ist würde die Zeit auf den Planeten möglicherweise viel schneller vergehen als auf die Erde, weil der schwarze Loch den Planeten beschleunigt und die Gravitation mit beeinflussen würde, also könnte es möglich sein das die Zeit auf einem anderen Planeten 10 mal schneller vergeht als auf die Erde richtig ?

Ein Raum ist 10 Meter lang.

In der Mitte ist eine Lichtquelle,
an den gegenüberliegenden Wänden jeweils ein Schirm.
Zwei Uhren mit der gleichen Uhrzeit werden an die Wände angebracht, sie sollen die Uhrzeit messen wenn Licht auf das Schirm trifft.
Beobachter 1 befindet sich außerhalb des Raumes auf der Erde,
Beobachter 2 steht im Raum neben der Lichtquelle.
Vor der Relativbewegung sind für beide Beobachter x1 und x2 gleich lang,
und Uhr 1 und Uhr 2 zeigen die gleiche Uhrzeit an.
Der Raum beschleunigt in die Richtung wie im Bild zu sehen, bis er eine konstante Geschwindigkeit v erreicht.
Die Lichtquelle wird dann eingeschaltet.

Im Inertialsystem von Beobachter 1 müssten beide Uhren die gleiche Uhrzeit anzeigen, und x1 und x2 gleich lang sein. Das Licht trifft zuerst Schirm 1 dann Schirm 2, es legt eine längere Strecke zum Schirm 2 zurück und braucht länger.
Das heißt Uhr 1 zeigt eine frühere Ankunftszeit des Lichts an.


Im Inertialsystem von Beobachter 2 braucht das Licht die gleiche Strecke und Zeit zu beiden Schirmen, da Licht in jedem Bezugssystem die gleiche Geschwindigkeit hat.

Das steht aber im Widerspruch zu den Messergebnissen aus dem anderen Inertialsystem.


Wie sieht das im Inertialsystem von diesem Beobachter 2 aus?
Die Uhren gehen entweder anders oder x1 und x2 sind nicht gleich lang
x1<x2 / t1>t2 ?