Warum vergeht die Zeit schneller wenn man sich mit Lichtgeschwindigkeit bewegt?

Hallo argmnt,

vielleicht sollte ich als erstes auf den zweiten Halbsatz eingehen:

... wenn man sich mit Lichtgeschwindigkeit bewegt?

Geschwindigkeit ¹) ist immer Geschwindigkeit relativ zu ²) einem Bezugskörper.

An das Lichttempo ¹) c kommt ein Körper oder ein Teilchen mit Masse nur beliebig nahe heran, kann c selbst aber nicht erreichen.

Der im Folgenden beschriebene Effekt tritt aber auch nicht erst bei c auf, sondern grundsätzlich bei jedem Tempo, nur dass er sich unterhalb von 0,1c (was immerhin 30 000 km⁄s sind) kaum bemerkbar macht.

Warum vergeht die Zeit schneller ...

Die Formulierung ist etwas unpräzise. Wir brauchen zwei Ereignisse Ě₁ und Ě₂ und zwei Uhren, die zwischen genau diesen Ereignissen zwei unterschiedliche Zeitspannen messen, die wir miteinander vergleichen wollen.

Drei Raumfahrzeuge A, B und C mit ausgeschaltetem Antrieb schweben in einer Linie, die wir als x-Achse eines von B aus definierten Koordinatensystems Σ bezeichnen können. B selbst ist also bei x = 0. A und C sollen denselben Abstand d von B haben, d.h., A ist bei x = −d und C bei x = d. Natürlich sind alle Uhren in Σ synchronisiert.

Als Zahlenbeispiel verwende ich gern d = 2 lmin = 120 ls, das sind rund 36 Millionen km.

Du sitzt in einem vierten Raumfahrzeug B', das sich – ebenfalls mit ausgeschaltetem Antrieb – entlang der x-Achse bewegt, und zwar mit konstanter 1D-Geschwindigkeit v = 0,6c.

Die beiden Ereignisse Ě₁ und Ě₂ sind Dein Vorbeiflug an A und an B. Die Zeitspanne dazwischen muss nach der Uhr von B natürlich Δt = t₂ − t₁ = d⁄v = 200 s sein.

Die Spezielle Relativitätstheorie (SRT) sagt nun aus, dass Deine eigene Uhr zwischen denselben Ereignissen nur 160 s misst. Die Bewegung von A nach B geht für Dich also um 20% schneller, aber warum?

Das versuche ich im Folgenden zu erklären:

Wir haben A, B und C immer als stationär angesehen. Ebensogut könnten wir aber auch Dich als stationär und A, B und C als mit −v (gleiches Tempo, entgegengesetzte Richtung) bewegten Raum- Konvoy ansehen, also in einem von B' aus definierten Koordinatensystem Σ' rechnen.

Das Relativitätsprinzip (RP), das schon von GALILEI formuliert wurde, sagt dabei aus, dass sich durch diese Umdeutung an den grundlegenden Beziehungen zwischen physikalischen Größen (nichts anderes sind Naturgesetze) nichts ändert.

Nach GALILEI und NEWTON sind damit zunächst die Gesetze der Mechanik gemeint.

Zu den Naturgesetzen gehören allerdings auch die erstmals von MAXWELL formulierten Grundgleichungen der Elektrodynamik und damit auch die elektromagnetische Wellengleichung. Das besondere an ihr ist, dass sie anders als andere Wellengleichung ohne Bezug auf irgendein Medium direkt aus MAXWELLs Gleichungen folgt.

Deshalb sollte insbesondere auch die elektromagnetische Wellengleichung in Σ und Σ' dieselbe Form haben, oder, konkret gesprochen, was sich relativ zu ²) A, B und C mit c bewegt, das bewegt sich auch relativ zu ²) B', also relativ zu Dir mit c und umgekehrt.

Gehen wir jetzt einen Schritt zurück und rechnen in Σ, d.h., wir sehen B als ruhend an.

• Wenn B zu B' ein Signal schickt, sollte es mit 1 + v⁄c = 1,6 - facher Freqenz bei B' ankommen, da Signal und B' mit Differenztempo ²) c + v aufeinander zukommen. Das heißt auch, B' sollte die Uhr von B 1,6- mal schneller ticken sehen.
• Wenn B' zu B ein Signal schickt, komprimiert die Bewegung von B' die Wellenlänge des Signals auf das 1 − v⁄c = 0,4- fache, weshalb es bei B mit 1/(1 − v⁄c) = 2,5- facher Frequenz bei B eintreffen sollte. Das heißt auch, B sollte die Uhr von B' 2,5- mal schneller ticken sehen.

Schickt einer von beiden ein Signal mit der konkreten Absicht, ein Echo aufzufangen, wird dessen Frequenz um den Faktor

(1) (1 + v⁄c)/(1 − v⁄c) =: K² = 4

höher sein als die des ursprünglichen Signals.

Nun könnte man daran, wer die stärkere Freqenzerhöhung misst, feststellen, wer sich bewegt und wer nicht. Laut RP ist das aber gerade nicht möglich; der optische DOPPLER-Effekt muss symmetrisch sein, d.h., Jeder misst eine Frequenzerhöhung um den Faktor K = 2 und sieht die Uhr des Anderen doppelt so schnell ticken wie die eigene, solange beide sich einander nähern.

Aus der Perspektive von B' ist das um den Faktor 2÷1,6=1,25 "zu schnell", aus der Perspektive von B ist das um den Faktor 2÷2,5=0,8 "zu langsam".

Ich habe oben B' an 3 Raumfahrzeugen vorbei fliegen lassen. Das wirft die Frage auf, was das dritte, C, eigentlich soll.

Nun, die Raumfahrzeuge stehen alle in Funkkontakt. Besonders will ich dabei den Blick auf zwei Signale von A und C lenken, die B und B' im Augenblick t₂ ihrer Begegnung erreichen.

Rechnen wir in Σ, hatten die Signale beide die Strecke Δx = d zurückzulegen und sind daher beide offensichtlich zur Zeit t₂ − d⁄c abgeschickt worden, auch wenn Du als Beobachter auf B' aufgrund von Aberration C in der Entfernung K∙d (4 lmin) und A in der Entfernung d⁄K (1 lmin) siehst.

Rechnen wir allerdings in Σ', so ist diese Deutung nicht haltbar. Schließlich bist in Σ' Du der Ruhende, weshalb Du C bzw. A in der Entfernung siehst, in der C bzw. A bei Absendung seines Signals war (Retardierungseffekt). Daher hatte das Signal einen um K², also 4 mal längeren Weg zu Dir als das von A und muss entsprechend früher abgeschickt worden sein.

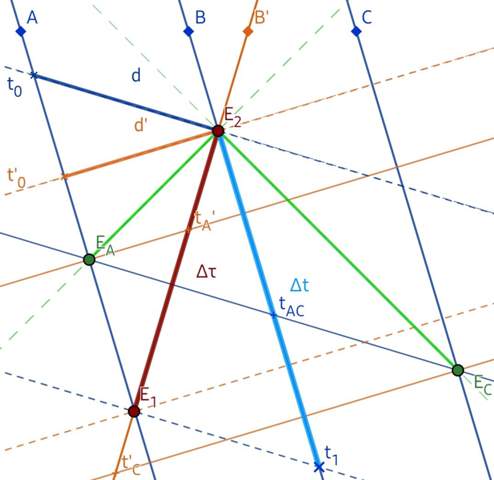
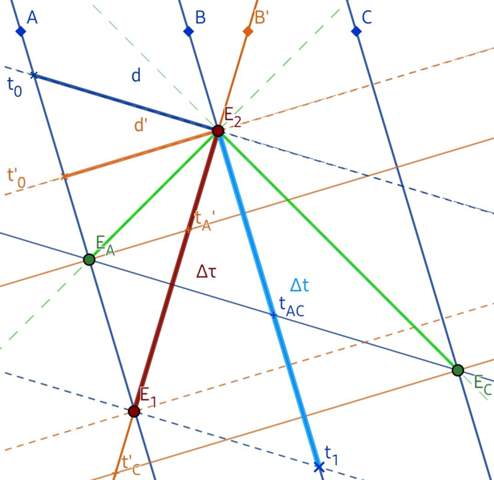
Abb. 1: Schematisches Raumzeit- Diagramm des Vorbeifluges von B' an A, B und C und umgekehrt. In Grün sind die Signale eingezeichnet, die B und B' bei ihrem Vorbeiflug gleichzeitig erreichen. Die gestrichelten Linien sind Linien konstanter Zeit, wobei die blauen für t=const. und die roten für t'=const. stehen.

__________

¹) Geschwindigkeit im engeren physikalischen Sinne ist eine Vektorgröße, eine Größe mit Richtung. Wenn wir uns gleich schnell bewegen, bewegen wir uns u.U. auch relativ zueinander; wenn wir uns relativ zu einem Bezugskörper mit derselben Geschwindigkeit bewegen, bewegen wir uns relativ zueinander gar nicht.

²) Mit "relativ zu X" ist immer gemeint, dass wir in diesem Zusammenhang X als stationär betrachten. Die Differenzgeschwindigkeit zweier Körper in Bezug auf einen dritten (den wir in diesem Zusammenhang als stationär ansehen) ist im Allgemeinen nicht dasselbe.

Man kann nicht pauschal sagen, dass die Zeit langsamer (nicht schneller) vergeht, wenn man sich schnell bewegt.

Wenn sich zwei Bezugsysteme aneinander vorbeibewegen, erscheint immer die eigene Zeit "normal" und die Zeit des andern gedehnt. Die Veränderung der (in der SRT jedoch flach bleibenden) relativen Raumzeit (Raum und Zeit gehören zusammen) ist aber eher mathematisch als bildlich zu verstehen (verschiedene Koordinatensysteme), d.h. das Resultat beim Berechnen des absoluten Wertes c (Lichtgeschwindigkeit) aus Weg durch Zeit bleibt in jedem Bezugssystem immer gleich.

Ich setz noch einen drauf. Von annähernd lichtschnellen Teilchen (kosmische Strahlung) aus gesehen, die auf die Erde zurasen, erscheinen wir verzerrt und annähernd lichtschnell. Merkst du was bezüglich Relativität?

Wenn jedoch ein Raumschiff von der Erde (die sich gleichförmig weiterbewegt) startet, beschleunigt (also Energie hineinsteckt), einen Bogen fliegt (Kreisbeschleunigung), verzögert (ist auch Beschleunigung) und wieder auf der Erde landet, wird sich beim Vergleich mit der Erde herausstellen, dass im Raumschiff weniger Zeit vergangen ist.

Tut sie nicht. Nur, wenn ich jemanden beobachte, der sich mit hinreichend hoher Geschwindigkeit an mir vorbeibewegt, messe ich (!!!), dass die Zeit im vorbeifliegenden System langsamer vergeht. Der, der im vorbeifliegenden Objekt mitfliegt, merkt von seiner Geschwindigkeit gar nichts und auch keine verkürzte Zeit.

Und um es auf die Spitze zu treiben. Dem, der an mir vorbeifliegt und mich beobachtet, geht es umgekehrt genauso.

langsamer, vom jeweils anderen Inertialsystem aus gesehen.

Die sogenannte Lichtgeschwindigkeit ist die Geschwindigkeit, mit der Realität sich ausbreitet. Nichts was Ruhemasse* hat kann diese Geschwindigkeit erreichen, und nur weil Photonen keine Ruhemasse haben, haben sie diese Geschwindigkeit, daher der Name.

Der Name kommt auch daher, dass man früher glaubte, das Licht brauche ein absolut stationäres Medium, in dem sich elektromagnetische Wellen ausbreiten (so wie Schallwellen in Luft), den sog. Äther. Die Frage, woran so ein stationärer Äther räumlich festgemacht sei, führte zum Michelson-Morley Experiment, bei dem eigentlich erwartet wurde, dass mit der Geschwindigkeit der Erde durch den Äther unterschiedliche Geschwindigkeiten des Lichts in unterschiedliche Richtungen gemessen würden. Überraschung: kein Unterschied, also kein Äther (es sei denn er würde zufällig ausgerechnet an der Erde festgemacht sein). Daraus geht nicht nur hervor, dass es keinen Äther gibt, sondern dass diese Geschwindigkeit eine in allen Inertialsystemen gleiche Naturkonstante und damit nicht überholbar ist, denn wenn man versucht den Strahl einer Taschenlampe mit dem Auto zu überholen, ist er relativ zum Auto genauso schnell wie relativ zur Taschenlampe.

Erst hier setzt die spezielle Relativitätstheorie an, die mit recht einfacher Mathematik (Lorentz-Transformationen) darlegt, was das für Auswirkungen auf Zeiten und Längen (und auch die kinetische Energie*) in bewegten Systemen hat.

*) Kinetische Energie von Objekten mit Ruhemasse enthält einen Term der Lorentz-Transformation wie Zeiten und Längen. Wenn man ein Fahrzeug in die Nähe der Lichtgeschwindigkeit beschleunigt, geht mit wachsender Geschwindigkeit ein immer größerer Anteil der zugeführten Energie in immer weniger Geschwindigkeitszuwachs und lässt für den äußeren Beobachter das Fahrzeug immer träger erscheinen - die Lichtgeschwindigkeit wird nie erreicht.

Die Zeit vergeht für jeden selbst immer gleichschnell, egal wie schnell er sich bewegt, zudem kann man die Lichtgeschwindigkeit nicht erreichen, nur annährend wäre theoretisch möglich. Trotzdem, auch in diesem Fall würde für den Reisenden die Zeit nicht langsamer ablaufen. Die Zeit des Reisenden würde nur für das ruhende Bezugssystem (z.B. für einen Beobachter auf der Erde) langsamer (nicht schneller) ablaufen, als seine eigene Zeit auf der Erde.