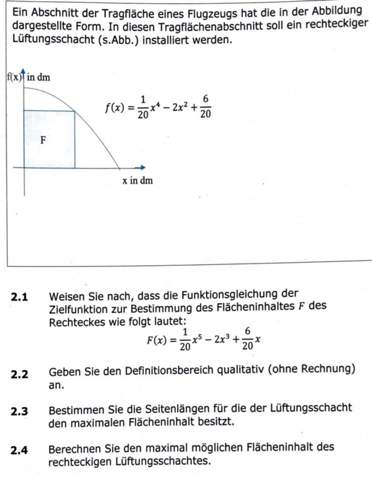
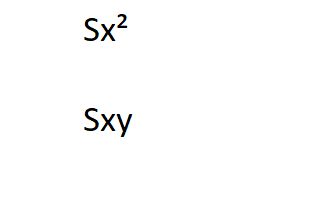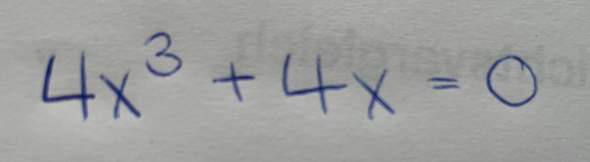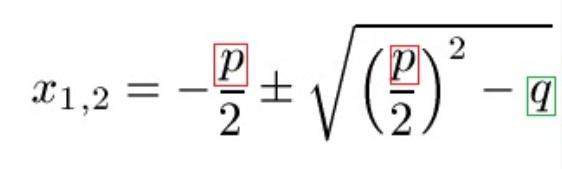Mit folgender Erklärung (aus einem englischen Text übersetzt):
---------
Der reiche Mann repräsentiert die Juden. Die Juden zur Zeit Jesu waren Nachkommen von Jakobs Sohn Juda. Der reiche Mann im Gleichnis hatte fünf Brüder, ebenso wie Juda, die alle von derselben Mutter, Lea, geboren wurden:
Ruben
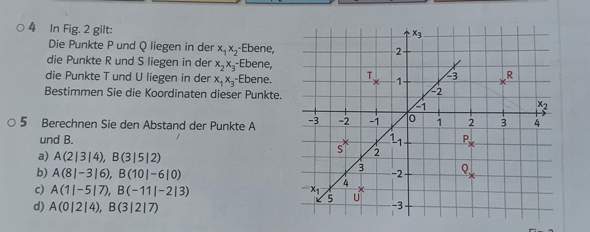
Simeon
Levi
[Juda war der vierte Sohn]
Issachar
Sebulon
Der reiche Mann war in Purpur und feines Leinen gekleidet und lebte jeden Tag in Luxus. Das Purpur und das feine Leinen repräsentieren die Farben und Stoffe des Königshauses und der Priesterschaft. All dies bedeutet, dass den Juden die Dinge des Reiches Gottes anvertraut wurden. Sie wurden vor allen anderen Nationen auserwählt und mit den „Kleidern“ und dem „Luxus“ ausgestattet, den Namen Gottes zu tragen, seine Absichten auf der Erde zu repräsentieren und sich seiner Segnungen und seines göttlichen Schutzes über der Nation zu erfreuen.
Die Juden wussten genau, wer dieser reiche Mann war, sobald Jesus ihn beschrieb.
Lazarus hingegen repräsentiert die umliegenden Nationen, die nur am Tor des reichen Mannes betteln konnten und sich danach sehnten, die Krümel spiritueller Wahrheiten und Segnungen Gottes zu essen, die vom Tisch des reichen Mannes fielen.
Nachdem Lazarus und der reiche Mann gestorben waren, wurden ihre Rollen vertauscht. „Tod“ bedeutet im Kontext dieses Gleichnisses eine grundlegende Veränderung ihrer Lebensumstände.
Den Juden wurde schließlich von den Römern verboten, irgendwo in diesem Land zu leben, und sie wurden unter den Nationen verteilt. Dies ist seit Jahrhunderten die „feurige Qual“ des reichen Mannes (der jüdischen Nation).
Die „Lazarus“-Nationen nahmen die Heilsbotschaft durch Jesus Christus freudig an, vor allem dank der Bemühungen des Völkerapostels Paulus. Seit dieser Zeit lebt Lazarus in „Abrahams Schoß“, dem Ort des Glaubens. (Überall in den heiligen Schriften wird Abraham als „Mann des Glaubens“ dargestellt).
Dieser Ort des Glaubens ist der Ort, an dem Gottes Absichten auf der Erde und sein Segen in einem Volk verwirklicht werden, das aus allen Rassen und Nationen gezogen wird, um den Leib Christi zu bilden. Wir alle werden zu metaphorischen „Abrahams“ – Männern und Frauen des Glaubens – wenn eine lebensverändernde Begegnung mit dem Herrn Jesus Christus zu unserer Errettung führt. So ruht Lazarus jetzt im Schoß des Glaubens.
Schon der Name Lazarus ist bedeutsam, denn er bedeutet „Gott ist meine Hilfe“. Gott hat den nichtjüdischen Nationen geholfen und diese Geschichte von Lazarus und dem reichen Mann zu einem hervorragenden Beispiel dafür gemacht, was Jesus meinte, als er sagte: „Die Letzten werden die Ersten sein und die Ersten die Letzten“ (Matthäus 19:30 und 20:16).