Wie funktioniert Aufgabe 9?
Hallo, wie funktioniert diese Aufgabe? Warum gibt es 6 verschiedene Graphen, obwohl überall die gleiche Gleichung steht?

2 Antworten
Du kannst aus einer Gleichung immer zwei Funktion machen. Beim ersten dann
f(x) = (x + 4)²
g(x) = 4
Diese zwei Funktionen kannst du dir zeichnen lassen.

Dann gucken welches Bild passt.
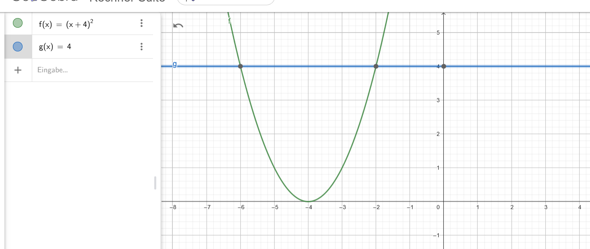
DANKE!! Ich hab das net verstanden mit den 2 funktionen aber ja stimmt so haben wir das auch gemacht
Das ist nicht einfach wenn du es ohne Taschenrechner lösen willst. Du brauchst sehr viel Wissen wie Funktionen aussehen können.
f(x) = (x + 4)²
g(x) =4
Scheitelpunktform für Normalparabeln ist s(x) = (x - d)² + e Dabei ist der Scheitelpunkt bei S(d |e ). Bei f(x) = ist e = 0 also ist der Scheitelpunkt bei S(-4 | 0). Die Parabel ist nach oben geöffnet weil der Streckfaktor positiv ist. [ Wäre der Streckfaktor negativ, stände da f(x) = - (x + 4)² ]
Es gibt nur eine Parabel mit dem Scheitelpunkt S(-4 | 0) und zwar im mittleren Bild oben.
Dann haben wir noch g(x) = 4. Das ist eine lineare Funktion. Allgemeine Funktionsgleichung ist g(x) = ax + b. Hier ist a = 0 und b = 4. Die Steigung ist also 0 und die y-Achse wird bei 4 geschnitten. Auch das passt zum mittleren oberen Graphen.
Aufgabe b) ist dann Lösungsmenge.
(x + 4)² = 4 Wurzel ziehen:
x + 4 = +-2
x1 = -6 und x2 = -2
------------------
Bei der dritten Gleichung hast du x² + 8x = - 12
Die x² steht für eine Normalparabel, nach oben geöffnet. Das +8 steht für die Steigung an der Stelle x = 0. Da würde eine Normalparabel mit dem Steigungsdreieck gemessen um +8 hoch gehen.
Die -12 steht für eine lineare Funktion, die die y-Achse bei -12 schneidet.
Passen tut dazu das Bild links unten.
Aufgabe b)
x² + 8x = - 12
x² + 8x + 12 = 0
Hier die PQ Formel anwenden mit p = 8 und q = 12
-------------
Gleichung 4) x² + 12 = - 8x
Hier hast du eine Normalparabel mit Scheitel auf der x = 0 Stelle oder auf der y-Achse. Die y-Achse wird bei +12 geschnitten.
Die Lineare Funktion g(x) = - 8x ist stark fallend und geht durch den Ursprung.
Das Bild links oben passt gut dazu.
Man muss erkennen können , dass (1) und (6) letztlich dasselbe ist
( mach mal +3 bei (6)
.
(1) ist b und (6) ist e
.
ich kann keine Zahlen bei x und y erkennen , aber bei b und e sollten die Schnittpunkte von Parabel und Gerade beide bei -2 und -6 liegen
.
.
vergleiche (2) und (5)
bei (2) sieht man links die Normalparabel (x²) und rechts eine Gerade mit Steigung -8 und b = -12
ergo gehört c dazu
.
egal ne ich vesrtehs nicht kannst du mal besser erklären das klappt irgendwie nicht