Was für eine Gleichung passt zu dem Graphen von Aufgabe c?

Answer 1

[gauss58]

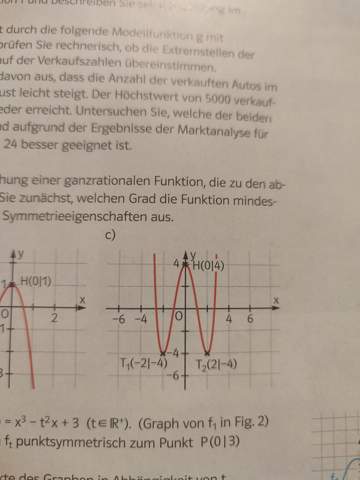
Der Graph der Funktion ist symmetrisch zur y-Achse und der y-Abschnitt liegt bei 4. Folglich passt: f(x) = a * x⁴ + b * x² + 4

Auch ist erkennbar, dass a positiv ist.

Werte für die Parameter a und b findest Du, indem Du die gegebenen Punkte und Extrema auswertest.

Es reichen die Bedingungen f(2) = -4 und f'(2) = 0 für die Bestimmung von a und b.

Answer 2

[evtldocha]

Folgende Funktion passt dazu:

$f\left(x\right)=\frac{1}{2}x^4-4x^2+4$

Wie kommt man da drauf?

• 4 reelle Nullstellen -> mindestens 4. Grad
• Achsensymmetrie -> keine Glieder mit ungeraden Exponenten f(x) =ax⁴ + cx² + e
• f(0)=4 -> e=4
• Ableitung f'(2)=0
• f(2)=-4

Aus den letzten beiden Bedingungen ergibt sich ein lineares Gleichungssystem für a und c.