Hi!

"Angewandte Statistik für Humanwissenschaften" ist das Modul, wovor ich mich so ein bisschen fürchte.

Ich bin eine absolute Niete in Mathe (gerade so durch die Abi Prüfung gekommen) und frage mich daher, ob es für mich überhaupt schaffbar wäre.

Das wären so die Inhalte:

- Erhebung von Daten (Studien und Umfragen)

- Graphische Darstellung von Daten (Säulendiagramme, Histogramme und Boxplots)

- Statistische Maßzahlen (Arithmetisches Mittel, Median) und Dispersion (Varianz, Standardabweichung und Interquartilsabstand)

- Lineare Regression, Kovarianz und Korrelation

- Begriff der Wahrscheinlichkeit, das empirische Gesetz der großen Zahlen

- Wahrscheinlichkeitsmaße

- Zufallsvariablen und Verteilungen

- Erwartungswert und Varianz

- Unabhängigkeit

- Gesetz der großen Zahlen und zentraler Grenzwertsatz

- Logik von Signifikanztests (Hypothesenbildung und –formulierung, Alpha- und Betafehler, Vorgehen bei Signifikanztests, Grenzen von Signifikanzaussagen (Stichprobengröße, Effektstärke, Power)

- Statistische Tests (t-Test, F-Test, Chiquadrat-Test)

Kann mir jemand bei dieser Aufgabe helfen? Ich verstehe nicht,wie sie geht!

Ich versteh die Aufgabe trotz Lösung nicht, kann mir jemand bitte erklären wie man da drauf kommt? Das erste Bild ist die Aufgabe und das zweite die Lösung. Danke!!

Kann mir jemand bei der Aufgabe b weiterhelfen?

Ich hänge gerade so ein wenig in der Luft wie die Terme für die Fläche und den Umfang der Figur

lauten.

Soweit bin ich, liege ich zufälligerweise richtig?

U= 2 × 2a + 2 × a + 2 × 4

U= 2 × (a + 4 + 2a)

U= 2a + 8 + 4a

U= 6a + 8

Hier komme ich nicht weiter:

A= 2a × (a+4)

A= ???

Also wenn man draufklickt, ist es lesbar.

Das ist jetzt keine Hausaufgabe, sondern von einer Schulwiederholung und ich blick die Sachen halb.

also ursprünglich Hätte ich einfach in der normalen Gleichung oben rechts x-2 eingesetzt, nicht mit abc, was dann irgendwie keinen Sinn gemacht hat, ich kapiere es nicht ganz, wieso soll man da abc einsetzen und nicht -2 10 -25 nehmen? Und woher soll man wissen, wann man das machen muss? Ist es einfach, weil abc gesucht sind, und y schon bekannt ist?

Und bei diesem gruppieren nach x2, etc, ich raffs nicht warum macht man das, ich dachte man soll es nicht nach x gruppieren, sondern nach (x-1), weil das y wäre? Und was hat das für einen Sinn, dass da die gemischten abc Zahlen vor einem x stehen? Ich raffs gerade überhaupt nicht

Ich sitze seit Stunden an dieser Aufgabe. Kann mir vlt jemand weiterhelfen mit Lösungschritten damit ich es verstehe? Wäre super nett! Ich brauche nur die erste Augabe die 2 habe ich verstanden!

Die Aufgabe war es eine 2x2 obere Dreiecksmatrix (A) sowie eine Diagonalmatrix (D) derselben Dimension zu Multiplizieren (also einmal A*D und einmal D*A) und das Ergebnis zu interpretieren. Ich habe das gemacht (siehe Foto), aber verstehe nicht genau was man da alles interpretieren kann außer dass die Hauptdiagonale bei beiden gleich ist und wieder eine obere Dreiecksmatrix rauskommt?

Ich hab mal einen Film gesehen, in dem es so etwas wie ein Fahrstuhl gab, der bis hoch hinaus ins Weltall reichte und oben war dann noch eine Plattform drauf, wo sich die Gäste aufhalten und die Sicht auf die Erde von oben genießen konnten. Wäre ein solches Bauprojekt in die Realität umsetzbar oder wär dies allein schon von der Statik her nicht möglich?

Hallo,

ich brauche Hilfe bei dieser Aufgabe:

In einer Jugendherberge gibt es einige 4 Bett Zimmer und doppelt so viel 6 Bett Zimmer .In der Jugendherberge haben 112 Schüler/innen Platz.

a) Stelle ein lineare Gleichungssystem auf und berechne die Anzahl der 4 Bett Zimmer und 6 Bett Zimmer

b) In der Klasse G9d gibt es 15 Schülerinnen und 13 Schüler. Tim behaupt ,dass die Klasse höchstens 6 Zimmer braucht. Stimmt es ? Erkläre begründet.

LG

124 ist kg klar, 6 ist gram klar aber welche Einheit ist die 5?

|4x − 8| < |2x + 2|
Wie löst man diese Betragsungleichung bzw. welche fälle werden beachtet?
Ich bitte um Hilfe und bedanke mich jetzt schon!

Hallo ich stehe auf dem Schlauch. Ich möchte einen Essigreiniger zum desinfizieren herstellen. Im Internet steht 1 Teil Essig, 2 Teile Wasser. Ich möchte 500ml herstellen. Wie viel Essig und Wasser brauch ich?🙈

Ein Mopedfahrer benötigt für eine bestimmte Strecke 95 min, wenn er durchschnittld 35 km/h fährt. Um wie viel Minuten verkürzt sich seine Reisezeit, wenn er nach 15 min um 5 km/h schneller fährt?

Ich habe noch 3,5 Monate bis zum Halbjahr? Ich habe dennoch Angst um meine Noten. Denkt ihr es ist Möglich von einer 3 zu einer 2 zu kommen oder von einer 4 zu einer 3?

Kann den mal bitte jemanden erklären. Ich brauche ihn wahrscheinlich morgen für mein Praktikum in der Steuerkanzlei

Kann mir jemand vielleicht bei der Aufgabe helfen? Ich denke man muss da mit Brüchen rechnen richtig?

könnte mir jemand die Aufgabe vernünftig erklären anhand eines Beispiels damit ich sie besser bearbeiten kann???

Ausgangsfunktion: f(x)=x^3-4x+1

Endfunktion: g(x)=8x^3-8x+1

Woher weis man das diese Funktion mit Faktor 0,5 in x-Richtung gestreckt wurde?

Hallo

Ich möchte wissen wie oft man diese Kiste aufmachen muss um die 0.01% Belohnung zu bekommen

wäre so lieb bin so verzweifelt

kann mir wer erklären wie ich das Maximale Volumen eines A4 Blattes berechne

Ich habe die gleichung 13d mod 72 = 1

Wie löse ich sie? Danke im voraus

Kann mir jemand bitte detailliert die Lösung erklären ?

Ich habe für beta: 67° für. Für b habe ich 7,06 cm und für c habe ich 7,66cm. Sind diese Ergebnisse richtig bzw. Könnt ihr mir bitte ein Rechenweg rechnen mit diesen Angaben mit Ergebnis?

Aufgabe: In einer empirischen Untersuchung wird geprüft, ob ein Zusammenhang zwischen blonden Haaren und blauen Augen bzw. blonden Haaren und dem Geschlecht besteht. Von 842 untersuchten Personen hatten 314 blonde Haare. Unter den 268 Blauäugigen waren 121 Blonde. 116 von 310 Mädchen waren blond. Überprüfen Sie die untersuchten Zusammenhänge rech

nerisch.

Meine Lösung : P(blond)=PBA(blond)

P(Blond)=314/842=37% PBA(Blond)=121/268=45%

Eine Frage zu den blonden Haaren und blauen Augen . Habe für Blonde Haare 37% raus und für die blauen Augen 45% wie untersuche ich die Zusammenhänge hier rechnerisch? Bitte schritt für Schritt erklären.

Wie kommt hier 0,5 in der Klammer vor dem x zustande? Kann mir jmd. erklären wieso in der Lösung bei k 0,5 steht ?

Weiß jemand wie hier k (0,5)zu Stande kommt? Und wieso ist die Amplitude negativ und nicht positiv?

Hallo, Könnte mir hier jemand helfen ? Ich schreib bald eine Mathearbeit und diese Aufgabe soll wichtig sein. Es wäre sehr hilfreich vielen Dank

Danke:)

Zum Besipiel 70 Jahre in Stunden, Minuten und Sekunden

Guten Nachmittag!

Ich habe leider immer noch starke Probleme mit dem ausklammern und umstellen von Formeln in Mathe. Meine Lehrerin hat zum Beispiel diese Rechnung beim ersten Schritt wie anhegeftet ausgeklammert. Aber leider scheitere ich schon dabei den ersten Schritt nachzuvollziehen. Könnte mir bitte jemand Schritt für Schritt erklären was hier genau getan wurde und gibt es tips damit ich auch so schnell ausklammern kann? Weil ich oft schon bei Schritt eins scheitere.

Guten Tag ich brauche Hilfe eine Funktion zu zeichnen

Aufgabe 4a

Danke für eure Hilfe

Hey, kann mir da vielleicht wer helfen bei dem Vektor?

Warum geht es bei Aufgabe c) nicht auf, wenn man Erlöse - Gesamtkosten rechnet?

Also: (450 • 18) - (3755 + 168)? Da kommt ja 4177 € und nicht 1321 € raus? Wieso geht das nicht auf?

Danke!

Guten Tag

Wäre sehr hilfreich wenn mir jemand bei dieser Aufgabe helfen würde:

In einem Bücherregal stehen fünf französische, sieben spanische und elf englische Bücher. Auf wie viele Arten lassen sich zwei Bücher in verschiedenen Sprachen auswählen?. Lösung: (5über1)∗(7über1)+(5über1)∗(11)+(7über1)∗(11über1)=167.

Mein Problem: Ich weiss einfach nicht, wie ich auf diesen Rechenschritt kommen soll. Ist das ein bestimmtes Verfahren?

Sollte ich mich zu einem bestimmten Thema besser reinlesen damit ich diese Aufgabe verstehe? Wenn ja welches? (Was Kombination und Variation bedeutet, weiß ich)

Danke für jede Hilfe!

Hey

Ich brauche hilfe mir dieser Aufgabe

Ich hab kein plan wie ich es aufschreiben soll

So soll dann die Tabelle aussehen ungefähr

Danke

Die Oberfläche eines Kegels beträgt 680 Quadratzentimeter.Der Durchmesser ist 17 cm. Wie berechne ich damit die Länge der Mantelline s?Danke

Es geht um Sinus, Cosinus und Tangens, schonmal zur Info:)

Hallo, wir haben in der letzen Mathestunde eine Aufgabe zusammen an der Tafel bearbeit und ich habe die Aufgabe nicht verstanden, mir aber zum Glück den Lösungsweg mit aufgeschrieben. Nun ist es Zeit das zu überarbeiten, vorallem, weil ich sowas ähnliches jetzt bei den Hausaufgaben auch machen muss!

Wenn ich sin/cos/tan(a) schreibe meine ich mit a natürlich Alpha🙈

Gegeben war Tan(a)=¾ und die Formeln 1=sin²(a)+cos²(a) und tan(a)=sin(a)÷cos(a).

Die Aufgabe war es, sin(a) und cos(a) herausfinden:]

Also, an der Tafel stand folgendes (99% davon habe ich verstanden, nur eine kleine Umformung nicht, die ich gerne verstehen würde;)):

Sin(a)÷cos(a)=¾ |×cos(a)

Sin(a)= ¾×cos(a)

✅️ bis hier hin alles verstanden. Dann:

1=(¾×cos(a))² + cos²(a) (✅️ verstanden)

1= 9/16×cos²(a)+cos²(a) = cos²(a)×[9/16+1]

(❌️ nicht verstanden. Also das nachdem ersten = kann ich mir noch irgendwie zusammen reimen (aber warum darf ich ¾ und cos(a) alleine quadrieren?). Aber das nach dem 2. = verstehe ich komplett nicht mehr. Wie aind wir von 9/16×cos²(a)+cos²(a) auf cos²(a)×[9/16+1] gekommen? Warum ist die Klammer aufeinmal eckig? Wo kommt die +1 vorallem her? Ah

Naja, und der Rest macht wieder mehr Sinn für mich, aber so ging's weiter:

1=25/16×cos²(a) |÷25/16 (=×16/25)

16/25=cos²(a) |Wurzel ziehen

Cos(a)=⅘

(✅️ macht wie gesagt Sinn. Und auch wie ich dann Sin(a) ausrechne, versteh ich ganz easy. Nur im Mittleren Teil kann ich wie gesagt nicht so ganz folgen..)

Vielen Dank für's lesen, ich hoffe mir kann hier jemand weiter helfen!☺️

Ich verstehe die Aufgabe 1. a) nicht.

kann jmd. mir bitte helfen.

das wäre sehr nett :)

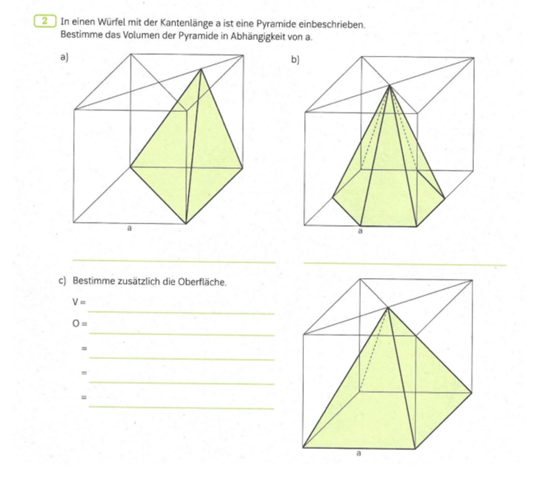
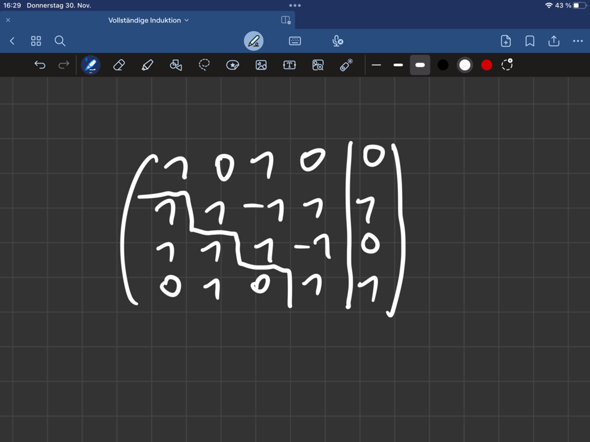
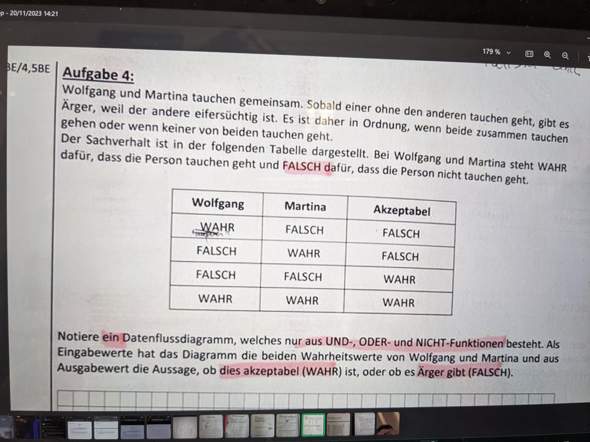
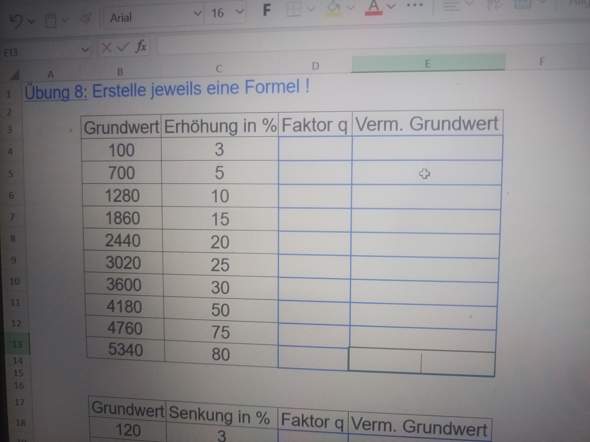
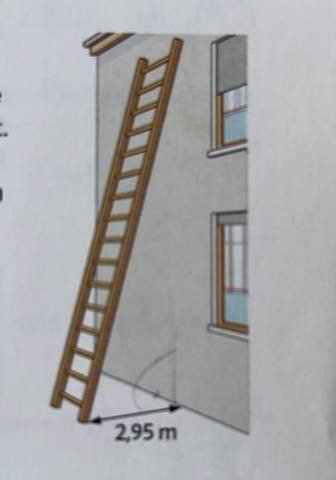
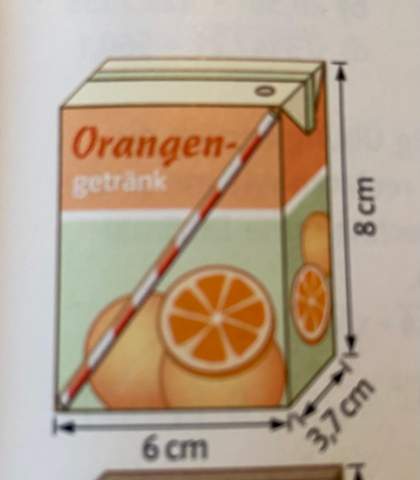
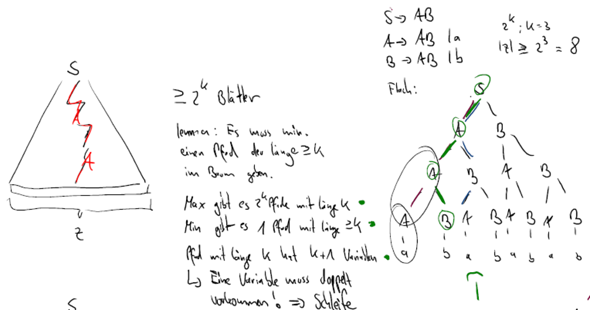
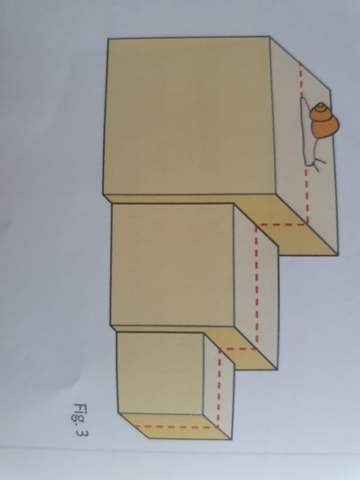
Ist diese Klassenarbeit in Mathe (Geometrie) einfach oder schwer?

Nach welchen Schulniveau sieht diese Klassenarbeit aus?

Sieht diese Klassenarbeit nach Klasse 10 aus? Ist diese Klassenarbeit für die 10. Klasse angemessen?

Sieht diese Klassenarbeit nach einen Realschulabschluss aus?

Wo gibt es hier Transferleistungen und Logische Denken?

Unser Lehrer hat gesagt, das er meint, es ist eine schülerfreundliche Arbeit. Ist diese Klassenarbeit wirklich schülerfreundlich? Wenn ja, warum?

In wie viel Minuten hätte man diese Klassenarbeit schaffen können?

Was ist die leichteste und die schwierigste Aufgabe?

Welche Wahlpflichtaufgabe ist leichter, Wahlpflichtaufgabe A oder B?

Welcher Teil ist einfacher, der hilfsmittelfreie Teil oder mit Hilfsmitteln?

Ist der hilfsmittelfreie Teil einfach oder schwer?

Warum gibt es in der Aufgabe 5b) einen Punkt für Folgefehler? Machen das auch andere Mathelehrer oder nicht?

Warum ist die Aufgabe 5a) nicht richtig gelöst? Wie hätte man diese Aufgabe lösen müssen?

Wie müsste man die Wahlpflichtaufgaben lösen müssen?

Muss man sich ärgern, dass man in dieser Klassenarbeit eine 2 geschrieben hat?

Hat der Lehrer diese Klassenarbeit streng oder locker gewertet?

Und bitte mit Begründung.

Gegeben ist S(1/-1) und P(3/-3) Wie heißt dann die Parabelgleichung?

Ich habe das während des Lockdowns Online gelernt, jedoch kann ich mich an nichts erinnern.

Hat jemand irgendwelche Tipps?

Könnt ihr irgendwelche Videos auf Youtube empfehlen?

Oder kann mir jemand bitte die Grundlagen beibringen?

Ich habe die lineare Funktion vor 2 Jahre in der Schule gemacht, jedoch kann ich mich an nichts erinnern und konnte auch damals das Thema nicht.

Denkt ihr es ist möglich die quadratische Funktion zu lernen, ohne die lineare zu wissen ?

Ich rechne gerade ein paar alte Übungsblätter durch und komme bei der Umformung auf dem Bild nicht weiter, genauer der Schritt von der zweiten zur dritten Zeile. Im ersten Schritt wurde nur der Term für sp(Q) eingesetzt. Grundsätzlich verstehe ich schon wie ausgeklammert wurde, jedoch weiß ich nicht, was mit den 3cos() passiert. In meiner Umformung komme ich auf 2cos() (durch den -cos() Term hinter dem Bruch), jedoch fällt dieser Teil halt nicht komplett weg. Dadurch wird der Termin am Ende nicht 0, weil dann ein anderer Faktor als 1 im Term mit a^2+b^2+c^2 steht(z.B. bei mir a^2+b^2+c^2-2).

Ich hoffe, dass ich das Problem verständlich erklärt habe und wäre um jeden Tipp dankbar.

ich habe gerechnet:

45 km (≠ von 54 und 36) geteilt durch 100≈ 4,5 km

60 min geteilt durch 100≈ 0,6 (≈ 36 sek)

also ist die Lösung 40?

ist lösung und rechenweg richtig?

vielen Dank für antworten

Habt ihr schonmal eine 6 gehabt? Und wenn ja bei welchem Fach

Hallo,

ich brauche Hilfe bei dieser Aufgabe:

Herr Kachel ist in fünf Jahren doppelt so alt wie sein heute 20 Jahre jüngerer Neffe Tobias. Wie alt sind die beide heute?

Meint man damit dass Herr Kachel in 5 Jahren doppelt so alt ist wie sein Neffe heute ist oder auch dass sein Neffe in 5 Jahren älter wird?

also : x+5 = 2y

oder x+5 = 2 • (y+5)

LG

Ich weiß, dass ich oben Shift+tan+0,5 eingeben muss, damit 26,57° rauskommen. Wie ist das aber unten bei -1,5 ?

folgendes ist gegeben:
A= (4,1)
B=(11,2)
C=(x,4)

Wie kann ich in Geogebra den x Wert herausfinden, bei dem der Winkel alpha 90 Grad hat?

Danke im Vorraus!!

Also dann dann nachdem man alle ergebnissr hat wieder in dezimal zahlen umwandeln

Ich komme bei der e nicht weiter kann mir jemand helfen ?

Hallo, Könnte mir jemand bei dieser Aufgabe helfen ? Vllt eine Rechnung sodass ich mir das selbst erklären kann vielen Dank im Voraus

Wir hatten gestern im Physikkurs unter anderem diese Aufgabe auf:

Und bekamen als "Hinweis" zur Lösung für "ob ein Marsmensch die Sonnenfinsternis beobachten kann" das, also mit Phobos (Ph):

Anscheinend muss man den Strahlensatz anwenden, allerdings verwirrt mich wie das mit der Lösung der Aufgabe zusammenhängt. Auch das x gefragt ist, allerdings ist x doch bekannt und zwar der Abstand zwischen Phobos zur Marsoberflache als 6000km plus den Radius von Phobos 10km also 6010 km. Es wäre ja dann x = dph - Mars

Wie gehe ich diese Aufgabe an?

Hallo ich bräuchte Hilfe bei der Aufgabe 3.2

kann mir jemand erklären was „zweite Winkelhalbierende“ ist und wie ich damit rechnen kann.

Schreibe bald meine erste englisch LK klausur.

Hat jemand eine klausur über non fiction analysis und könnte diese reinschicken?

Welches würdet ihr empfehlen? Falls es wichtig ist,es handelt sich um das Bundesland Bremen. ?

Um die Erde fliegen ja ca. 170.000.000 Teile Weltraumschrott und ich möchte ausrechnen, wie die Entfernung jedes Teils zueinander betragen würde, wenn wir sie alle gleichmäßig auf die Erdoberfläche verteilen würden (ignorieren wir dabei bitte, dass die Erde zu 70% mit Wasser bedeckt ist und behandeln es wie eine feste Oberfläche), wie rechne ich das genau aus? Und wie rechne ich daraufhin aus, wie die Entfernung jedes Teils zueinander in z.B. 400 km. Höhe betragen würde, auf welcher die internationale Raumstation ungefähr um die Erde fliegt? Kann mir da jemand helfen?

In meinem Heimatland Bosnien und Herzegowina und außerhalb dieses Landes gibt es Leute die gerne das Gerücht verbreiten dieses Land hat keine 3.2 Millionen Einwohner und das dort unter 2.5 Millionen Menschen leben und im ein paar Jahren(im Jahr 2030) unter die zwei Millionen Bewohner sacken könnte und Beweise dafür liefern sie immer keine da sie selbst denken das sie schlauer als die Leute sind die solche Daten geben. Daher möchte ich nur wissen gibt es eine Möglichkeit selbst herausfinden wie viele Einwohner ein Land hat und wie macht man das?

Oberstufe 12 Klasse

Hallo,

ich brauche Hilfe bei dieser Aufgabe :

Zwei unterschiedlich lange Kerzen wurden gleichzeitig angezündet. Nach zwei Stunden hatten beide Kerzen die gleiche Länge. Die eine Kerze war nach insgesamt dreieinhalb Stunden ganz abgebrannt, die andere nach insgesamt fünf Stunden. Um wie viel Prozent war eine Kerze zu Beginn länger als die andere?

ICH MUSS DABEI BESTIMMMEN WOFÜR X UND Y STEHEN UND ZWEI LINEARE GLEICHUNGEN AUFSTELLEN.

LG

Hallo,

wir haben in der Schule das Thema sehr schnell behandelt und ich habe nicht verstanden weshalb der Algorithmus funktioniert. Ich kann ihn lediglich stupide anwenden. Kann mich vielleicht jemand erleuchten?

LG

hattet ihr heute mehr Pech, oder mehr Glück?

Gehen wir mal davon aus man hat es irgendwie geschafft einen Tunnel nach Amerika zu bauen. Wie lange würde man dann mit dem Auto brauchen ?

Ich habe beliebig viele Schnüre der Längen 2m, 3m, 4m, 5m, 6m, 7m und 8m. Mit welcher Kombination komme ich mit möglichst wenigen Schnüren auf 44m oder ein bißchen mehr?

Verwende möglichst lange Schnüre.

m = Meter.

Funfrage, aber vielleicht doch? :D

Halli Hallo,

mein Mann möchte nächstes Jahr den Logistikmeister machen.

Leider hatte er schon immer eine Schwäche in Mathematik und würde gerne wissen was für Themen da so drankommen? Ihr wisst schon. Um sich besser drauf vorzubereiten oder vielleicht sogar Nachilfe zu nehmen.

Hoffe auf Rückmeldung

LG Franceska

Hallo, ich kaufe mir das Buch ,,die illutsirerte kurze Geschichte der Zeit" von Hawking. Wollte mir weitere ähnliche Bücher kaufen. Vielleicht modernere Bücher, die nicht nur Fließtext, sondern auch Bilder haben. Gibt es gute emphelungen?

Ich habe es jetzt ungefähr 45 Minuten probiert, habe aber keine Ahnung, wie ich die Aufgaben ohne irgendwelche richtigen Längenangaben lösen soll.

Servus ich habe mich für eine Ausbildungsstelle als Industriekaufmann in einem großen Unternehmen beworben.

Ich muss jetzt also in den nächsten Tagen einen Online-Test machen, welcher wohl „sehr anspruchsvoll“ sein wird.

Als Themen kommen übliche Sachen wie deutsch-/englische Sprachkenntnisse und auch Mathe und BWL Kenntnisse.

Meine frage ist ob hier jemand Erfahrung hat bzw. weiß was für spezifische Aufgaben im Mathe und BWL Teil vorkommen werden (Deutsch und Englisch sind kein Problem für mich).

Wie kann ich mich am besten vorbereiten.

Sehr geehrter Herr Zug,

durch eine Stellenanzeige,die ich am 06.10.2023 gesehen habe,bin ich auf Ihr Unternehmen aufmerksam geworden und bewerbe mich hiermit um ein Praktikum als Erzieher.

Derzeit besuche ich die neunte Klasse der Herdeschule in Frankfurt und werde demnächst mein Realabschluss machen.

Seit langem interessiere ich mich für Kinder und ihre Erziehung. Im Internet habe ich mich im Bereich Erziehung informiert. Zusätzlich bin ich seit einem Jahr als Babysitter tätig und habe viele Erfahrungen gesammelt. Dazu habe ich zwei Geschwister auf die ich jeden Mittwoch aufpasse. Außerdem zeichne ich in meiner Freizeit viel und nutze meine Zeit kreativ aus. Ich habe ihr Unternehmen gewählt, weil Sie sehr bekannt ist und meine Schwester Sofia Ihr Kindergarten besucht.

Ich freue mich auf eine Einladung zum Vorstellungsgespräc.

Mit freundlichen Grüßen

Kerem Müller.

________________________________________

Das ist eine Klassenarbeit.

Ich würde mich freuen,wenn ihr sie bewerten und die Fehler korrigieren würdet.

+Da wurde noch erwähnt,dass die Mutter Lehrerin ist. Das hat er nicht erwähnt..

(Ist nicht meins)

Danke für eure Antworten :)

Hallo,

ich habe die Aufgabe:

Bei einer Kartoffel-Milch-Diät möchte Herr Luft täglich einen Energiegehalt von 1800 kcal zu sich nehmen. 100 g Magermilch enthalten 3,5 g Eiweiß und 50 kcal; die gleiche Menge Kartoffeln enthält 2g Eiweiß und 70 kcal. Der tägliche Eiweißbedarf liegt bei 50g

Herr Luft versucht zu berechnen, welche Menge an Milch bzw. Kartoffeln er täglich zu sich nehmen müsste, damit einerseits sein täglicher Energiebedarf gedeckt ist, andererseits auch der Energiegehalt eingehalten wird. Zeige, dass dies jedoch unmöglich ist.

x wäre tägliche Menge an Milch pro 100g

y wäre tägliche Menge an Kartoffeln pro 100g

Was bedeutet hier pro 100g und warum ist es pro 100g

LG

Könnte mir jemand beim lösen dieser Aufgabe helfen. Vllt eine verständliche Rechnung wo ich mir das selbst mit erklären könnte. Das wäre sehr nett.

Moin,

Folgende quadratische Rechnung, um letztendlich die pq formel Nutzen zu können:

f(x) = -0,05x^2 + x + 40 -> | : (-0,05)

Lasse ich das x als x stehen? Oder soll ich mir das x als 1x vorstellen, sodass am Ende -20x rauskommt?

Welches Ergebnis ist nach der Rechnung richtig?

= x^2 + x + 800

Oder

= x^2 - 20x + 800

Danke

Heyy, es gab auf Youtube ja den Film vierzehn. Jetzt finden ich nur noch den Trailer. Kann man den Film noch irgendwo kostenlos schauen? Und ich habe mit bekommen, dass es eine Fortsetzung gäbe?

Hallo, könnt ihr mir bitte bei diesem Beispiel helfen, ich verstehe es leider gar nicht.

Danke im Voraus,

qMath34

Hallo,

Wie rechnet man diese Aufgaben?
Ich würde mich über ein Beispiel freuen!

Moin, habe gerade keinen Zugang zu Lösungen oder sonstiger Hilfe.

Könnte mir jemand diese Text Aufgabe als Gleichung aufschreiben und diesen nach x auflösen?

"Zieht man von 45 das Dreifache einer gesuchten Zahl ab, so erhält man die um 10 verminderte Zahl"

Danke & Liebe Grüsse

Hallo ich brauche Hilfe bei dieser Aufgabe wir sollen es nach der Additionsverfahren auflösen aber ich komm nicht weiter

Lg

Hallo Leute,

Ich bin komplett überfordert in Mathe. Die einfachsten Aufgaben bekomme ich nicht hin. Seit der Grundschule habe ich extreme Probleme in Mathe und schreibe nur 5er und 6er. Nachhilfe bringt bei mir nichts.

Normalerweise lerne ich neue Dinge recht schnell bloß in Mathe komm ich nicht voran. Es ist sehr frustrierend. Ich lerne Stundenlang und mache keine Fortschritte.

Nicht nur in der Schule habe ich Probleme in Mathe, sondern auch im Alltag. Sobald Zahlen im Spiel sind, bin ich überfordert. Egal wie sehr ich mich anstrenge es bringt nichts.

Wisst ihr vielleicht wie ich mich verbessern kann?

Kann mir einer helfen, wie ich rein rechnerisch hier zum Funktionswert von Sinus an dieser Stelle komme?

Ist es nicht so, dass es sehr schwer ist, dass selbst zeichnerisch in einem Eimheitslreis zu ermitteln, da man ja kaum genau wissen kann wo genau (-pi/6) ist oder?

Ich bin in Siebten Klasse und lebe sächsischen Schulsytem. Ich habe schon 6 Einsen und wenn ich 10 Einsen hab kriege ich was von mein Eltern. Meine schlechteste Note ist aktuell 12.10.2023 eine "4" in einer Deutsch Lk . Nun möchte ich die restlichen 4 Einsen bekommen, Ich habe eine Lernmethode entwickelt und zwar in folgenden Schritten:

1. Wenn die LK angekündigt wird: Erstmal grob alles durchlesen und in Kopf durchgehen.

2. Videos schauen:

Ich schaue wenn ich sch Abend im Bett liege schaue ich mir bis zu 5 Videos zu diesem Thema an.

3. Lern Übersicht auf einen Blatt erstellen:

Ich erstelle erst Stichpunkte, und später schreibe ich das ordentlich auf eine ,,MindMap" .

4. Abends in Hefter schauen

5. Vor der LK nochmal alles aufschreiben ("von der Hand in denn Verstand")

Was sagt ihr?

Ich möchte alle Funktionen zu einer Trendlinie zusammenfassen oder zumindest zu einer einzigen Funktion, jedoch kann ich nur für je eine Funktion eine Trendlinie erstellen. Weiß jemand, wie ich alle Funktionen vereine?

Wenn ich den Wert 6,7 habe und wissen möchte, wie viel Prozent davon der Wert 6,4 beträgt?

Danke für jede Hilfe :)

Kann mir jemand erklären wie dass geht? Die Aufgabe davor handelte von Binomischen Formeln

Hallo

Warum ist es nicht möglich 4 Geraden mit 2 Schnittpunkten zu zeichnen?

Heyy

Ich habe eine frage wegen mathe kann mir die jemand beantworten ?

👇👇👇👇👇

LG 🥰 vielen Dank schon mal im voraus

Bitte mit Begründung :)

Hallo

Warum können 4 Geraden maximal 6 Schnittpunkte haben?