Brauche Ansatz (Geometrie - Dreiecke)?

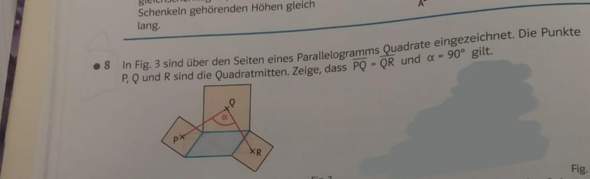
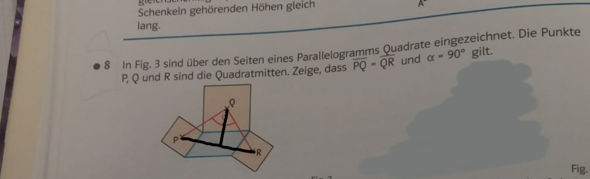
Bild zum Beitrag

Der 1. Schritt ist ja immer, Dreiecke suchen. Also wenn ich dann die Kongruenz von den beiden Dreiecken beweise, kann ich ja auch sagen, dass PQ und QR gleich groß sind und dann ist die Aufgabe fast gelöst. Wäre der Kongruenzsatz dann SWS? PM=MR ?? Wie soll ich das beweisen?

2 Antworten

Vom Fragesteller als hilfreich ausgezeichnet

ReimundAcker

Nutzer, der sehr aktiv auf gutefrage ist

im Thema Mathematik

29.11.2023, 01:26

Die gewünschten Eigenschaften lassen sich z. B. anhand der folgenden Figur zeigen:

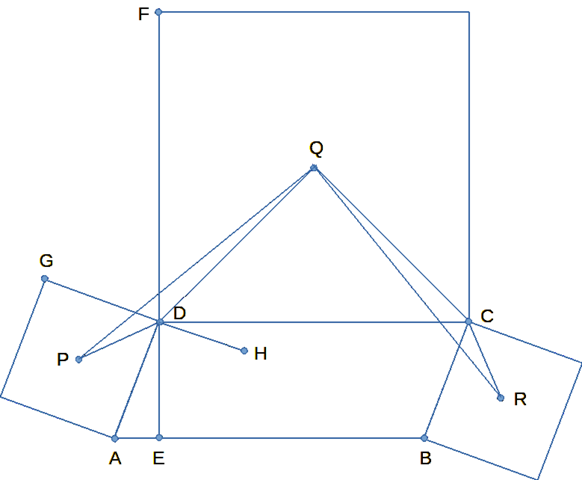
Bild zum Beitrag

Behauptung: ∢PQR = 90° und |QP| = |QR|

Beweis:

[1]  ∢QCR = ∢QCD + ∢DCB + ∢BCR
[2]  ∢QCD = 45°, da Diagonale im Quadrat die 90°-Ecken halbiert
[3]  ∢BCR = 45°, da Diagonale im Quadrat die 90°-Ecken halbiert
[4]  ∢QCR = ∢DCB + 90°     wg. [1], [2] & [3]
[5]  ∢QDP = ∢QDF + ∢FDG + ∢GDP
[6]  ∢QCF = 45°, da Diagonale im Quadrat die 90°-Ecken halbiert
[7]  ∢GDP = 45°, da Diagonale im Quadrat die 90°-Ecken halbiert
[8]  ∢QDP = ∢FDG + 90°     wg. [5], [6] & [7]
[9]  ∢DCB = ∢BAD, weil ggü.-liegende ∢ im ∥-ogramm =groß sind
[10] ∢BAD + ∢ADE = 90°, da ∢-Summe in 3eck = 180° & ∢DEA = 90°
[11] ∢ADE + ∢EDH = 90°
[12] ∢BAD = ∢EDH           wg. [10] & [11]
[13] ∢EDH = ∢FDG,          da Scheitel-∢ gleich groß sind
[14] ∢FDG = ∢DCB           wg. [9], [12] & [13]
[15] ∢QCR = ∢QDP           wg. [4], [8] & [14]
[16] |QC| = |QD|           halbe Diagonalen des Quadrats
[17] |AD| = |BC|, weil ggü.-liegende ∥-ogramm-Seiten =groß sind
[18] □ADG· um P ≅ □CB·· um R     wg. [17]
[19] |PD| = |RC|                 wg. [18]
[20] △QRC ≅ △QPD                nach SWS, wg. [15], [16] & [19]
[21] ∢PQD = ∢RQC                 wg. [20]
[22] ∢PQD + ∢DQR = ∢DQR + ∢RQC   wg. [21]
[23] ∢DQR + ∢RQC = ∢DQC
[24] ∢DQC = 90°, da Diagonalen in Quadrat ⊥ aufeinander stehen
[25] ∢PQR = ∢PQD + ∢DQR
[26] ∢PQR = 90°            wg. [25], [22], [23] & [24]
[27] |QP| = |QR|           wg. [22]
q. e. d.                   wg. [26] & [27]

Woher ich das weiß:Studium / Ausbildung – LMU München, Dipl. Math., eigene Recherche