Hallo,

ich fahre seit 5 Monaten Motorrad, bin allerdings erst seit kurzem wirklich auf Kurven aus. Als ich mit ein paar Freunden unterwegs war, waren diese viel schneller als ich. Wie kann ich Kurven schneller fahren?

Das Problem ist, dass ich zwar schon mit etwas Schräglage in dir Kurve gehe, aber mich nicht mehr traue, weil ich Angst habe wegzurutschen. Mein Freund meint, dass das bei trockener Straße ohne Öl oder so nicht passieren wird und ich ruhig tief runter kann, ist das so?

Ich fühle mich immer neben dünnen Mädchen zu dick, dabei bin ich nicht dick. Ich fühle mich aber dann immer wie ein trampel

Ich habe einen sehr schnellen Stoffwechsels und bin sehr dünn und weiß nicht ob ich zu nehmen kann.. ich würde gerne einen großen hintern und Brüste bekommen und weiß nicht wie ich möchte halt Kurven bekommen

Moin,

Soll man in kurven kein gas mehr geben oder die Geschwindigkeit einfach beibehalten?(Motorrad)

Brust =90cm

Taille =71cm

Po=100cm

Hüfte =85cm

Bin 12 Jahre alt.

Oder muss das nicht sein sie hat eine sehr schöne Rundung und breite Hüften heisst es das ich sie später vielleicht auch kriege oder kann ich sie auch von der familie meines vaters erben? Und was ist da aber wahrscheinlicher

moin moin meine Lieben,

Ich habe wie bestimmt sehr viele auch während der Corona Zeit viel Sport getrieben (davor zwar auch aber nicht regelmäßig)

jetzt ist mir aufgefallen dass meine Kurven sprich Taille, Hüfte etc. nicht mehr so vorhanden sind wie davor. Liegt das am Sport? Wenn ja, was kann ich tun damit ich meine Kurven wieder bekomme?

Wäre echt ein Traum wenn jemand dazu eine Lösung hätte

Kuss geht raus <3

also ich meine breitere Hüften welche Übungen und was hilft bei Hip dips?

Hallo ,

ich bin 170cm ,habe eine Maße von 89-68-94 und Wiege 57kg . ich wollte fragen welche Maße man haben muss und wie viel man wiegen muss um kurvig zu sein ohne dick zu erscheinen? Also dünn -kurvig ?

Hi,

findet ihr meine Beine zu dünn ?

Ich bin 16 wiege 53 Kilo und bin 1,62 groß.

Wie kann ich zunehmen, am Po und mehr Kurven bekommen ?

Kann ich durch Sport so aussehen ?

Kennt jmd irgendwelche Push ups oder sowas womit man so eine Hüfte bekommt ? Am besten von Amazon

Also wie kann man solche Kurven bekommen (durch bestimmte Hilfsmittel oder so?)

und denkt ihr sie hat sich an den Seiten etwas reingesteckt zb Kissen oder sowas ? Wenn ja was könnte es sein?

photoshop ja nicht da es auch so in videos ist .

Also ich weiß dass es eine etwas dumme Frage ist, aber kann man an den Kurven abnehmen? Ich mag meine Kurven einfach nicht. Kann mir bitte jemand weiterhelfen?Danke.

Weiß jmd wie man solche Kurven wie dieses Mädchen da bekommt ?

(sie meinte das es bei ihr durch Gene so ist)

das Mädchen ist übrigens 14

Das ist 100% natürlich da ich die Person kenne aber wie bekommt man bitte so einen schönen Körper? Sie ist 1.58.
Ich hingegen 1.66 und wiege 60kg Kann ich so ein Körper bekommen mit Sport und Ernährung oder eher unwahrscheinlich. Meine Körper ist nicht so Curvy wie ihr aber auch nicht Mega Brett sondern so das Mittelding.

Warum sieht man meistens durch keine Kurven, kindlicher und jünger aus? Bei mir ist es der Fall und dazu kommt noch dass ich sehr schlank bin. Und was kann man tun das man etwas älter aussieht hab schon Sport getrieben hilft nicht

Ich fühle mich einfach nicht weiblich genug. Ich bin 19 und relativ klein (1,55m). Ich wiege 44 Kilo und bin zierlich gebaut, ich sehe einfach nur kindlich aus :( ich wollte bald mit dem Sport anfangen aber ich weiß auch nicht welche Körperteile ich trainieren sollte und wie. Mit meinen Brüsten bin ich eig zu Frieden. Ich trage zwar Körbchengröße A aber sie wirken groß, da mein Körper zierlich gebaut ist. Naja, jetzt wäre meine Frage ob man durch OPs Kurven bekommen könnte. Ich möchte es erstmal mit dem Sport versuchen aber wenn es nicht klappt, bin ich bereit mich zu operieren.

Hallo Leute!

Ich habe den A1 Schein gemacht.

Meine Maschine ist die WR 125 X.

In der Fahrschule bin ich eine Duke gefahren und den einen Tag haben ein Kumpel und ich Mal getauscht, der die Duke hat und es fühlte sich wie der Himmel an.

Ich habe die Kurven gefühlt alle mit 20 km/h mehr als normal runtergerissen und fühlte mich so unglaublich sicher.

Zurück auf meiner Maschine fühlte ich mich sehr steif und bin die Kurven irgendwie schlecht gefahren, was ich aber erst nach dem Wechsel merkte.

Könnt ihr mir ein paar Tipps geben, wie ich mich auf der Maschine nicht so unsicher fühle?

LG

Jamie

Hi!!

Wollte mir heute eine Hose aus dem Wäschekorb nehmen da sind mir extrem dünne String tangas meiner mutter aufgefallen sie ist 48 Jahre alt warum trägt sie sowas??

Ich habe eine Stock Figur, egal wie viel ich wiege. Und ich meine damit nicht von der Seite, da ist eigentlich alles soweit ok, ich meine von vorne. Keine kurven, nichts. Zunehmen bringt auch nix, da ich überall speck ansetze und dann trotzdem noch keine kurven habe. Ich hätte gerne eine schmale Taille und ein breiteres runderes Becken. Kann man das mit Training überhaupt erreichen? Egal wie hart, ich will nur wissen ob's überhaupt geht, weil sonst muss ich mir die Mühe ja nicht machen, wenn das eh nichts bringt... Danke schonmal.

Es geht um seinen sehr speziellen Fall der bei mir heute zum ersten Mal aufgetreten ist und vielleicht auch nicht vorkommen sollte wenn man keine Fehler macht. Also es geht um Steckbrief-Aufgaben, das heißt ich muss von Informationen übe den Graphen zu seiner Funktionsgleichung kommen. Mein Problem ist, mein Graph einer ganzrationalen Funktion 4. Grades Achsensymetrisch ist. Das heißt seine generelle Funktion lautet f(x)=ax^4+bx^2+c

Ich habe genau 3 Informationen, das heißt ich sollte die Aufgabe lösen können. Die ermittelten Informationen sind f(0)=90, f(195)=0 und f'(0)=0

Wenn ich Jetzt die erste Ableitung bilde um eine Gleichung für die dritte Information zu erhalten dann komme ich auf f'(x)=4ax^3+2bx

Und hier kommt mein Problem, wenn ich jetzt die Information einsetzte komme ich auf die spektakuläre Gleichung 0=0 die mir nicht weiterhilft. Somit habe ich nicht genug Informationen. Ich erwarte nicht, dass irgendjemand mir helfen kann, aber wenn jemand eine Idee hat, nur raus damit. Vielleicht bin ich ja gerade auch nur dumm und die Lösung ist total offensichtlich...

Hallo, gestern war ich auf einer Geburtsparty und dort waren auch die zwei Mädchen aus meiner Jahrgangsstufe mit den krassesten und geilsten Kurven. Darunter hatte die mit dem schönsten bzw. knackigsten Po eine Leggins dran... Das ich ihr unauffällig 24/7 auf den Hintern geguckt hab, ist klar.Auf jeden Fall als wir dann alle in einem Zimmer waren und das Mädchen vorne gestanden ist, hab ich halt ihre richtig geilen Kurven und ihren Arsch von der Seite bzw. Hinten gesehen, als die anderen gestanden sind und ich auf der Couch gesessen bin. Jetzt meine Frage: Es fällt mir wirklich VERDAMMT schwer nicht einfach aufzustehen und ihren Arsch einfach durchzukneten. Weiß wer bis ich den Drang wegbekomm??? (ich habe keine Freundin und bitte keine Antworten wie "über was denkst du denn da nach? oder wie Kommst du denn auf sowas?"...)

Hey bin w/16 und für mein Alter Kurvig. Nicht dick. Bin 1,69 und wiege 65 kg. Ist gerade noch so ok. Seit dem ich halt in der Pubertät bin habe ich halt zugenommen.

Meine Figur ist UNGEFÄHR so : die oberschenkel sind etwas dünner aber mein Becken,Hüfte sind auch so.

Welchen Bikini würdet ihr mir da empfehlen und was denkt ihr steht einer Frau/Mädchen mit so Kurven ?

hey, mein Gürtel ist leider kaputt gegangen und nun suche ich verzweifelt nach einen Gürtel mit eckiger Schnalle, leider gibt es bei uns niemanden in der nähe, der mir so einen individuell anfertigen könnte. Deshalb wollte ich wissen, ob ihr wisst, wo ich mir in einem Online shop einen bestellen kann.

Hier ist ein Bild, wie dieser aussah:

Danke für eure Hilfe!

Hey

könnt ihr mir hier helfen?
würde gerne wissen, wie ihr das erklären/beschreiben würdet!
LG

Hallo Abend an alle.

Es gibt ein Mädchen auf unserer Schule die keine jungfrau mehr ist das wissen schon viele.Dann meinte einer so deshalb hat sie solche Kurven also ich weiß nicht was genau er gesagt hat jedenfalls etwas mit Kurven und dann meinte ein anderer das frauen die schon sex hatten dann solche dünne Kurven haben.Ich kenn mich ehrlich gesagt nicht aus aber ich wollte fragen was passiert bei Mädchens die Sex schon hatten mit den Kurven und woran kann man noch erkennen das ein Mädchen keine jungfrau mehr ist?

Außer das sie schon Ahnung damit hat.

Hallo,

gestern war ich auf einer Strecke unterwegs. Wenn ich das Lenkrad vollständig auf der Kurve einschlage, ging das nicht? Die Straße hat Zweibahnen.

Hallo hallo 😊 ich wollte euch mal etwas fragen. Weiß jemand, ob solche Hosen von Factu oder Pitbull auch in Deutschland verkauft werden? Ich suche sie hier schon seit langem. Oder vielleicht gibt es deutsche Marken, die Jeans in ähnlicher Form anbieten?

Jede Frau ist anders, ich weiß schon. Aber wie findet ihr es am besten?

Also mögt ihr es, wenn man nicht nur die Brüste und den Arsch anfasst, sondern auch so über die Kurven des gesamten Körpers streicht? Ich (m) finde es mega geil.

Ja die Frage ist seltsam, egal.

heyy

bin 1,65 und wiege 55kg .

ich möchte zunehmen also curvys bekommen und ja ich werde mit den nachteilen davon leben aber sehe halt sehr „krank“ aus weil ich so dünn bin..

danke im voraus für die tipps 🤗

Hallo!

Ich bin 171 cm groß und wiege 51 kg. Eine Freundin ist 165 und wiegt 64 kg und sie behauptet ihre Figur ist viel schöner weil sie Kurven hat. Was findet ihr schöner mein Gewicht oder ihr Gewicht

Brüste lieber oder den Po einer frau.

Würde ich weiblicher aussehen wenn ich von 57 kg auf 60-61 Kilo hoch geh? Bei na Größe von 177. Hab ziemliches Flachland und hätt einfach gern mehr Kurven. Würde Natürlich auch den nötigen Sport dazu treiben (waist Workouts usw)

Oder wäre ich dann dick?

Hi,ich trainiere sehr gerne meinen Hintern und hab auch einen ziemlich schönen würde ich sagen☺️

Nun würde ich gerne wissen,ob ihr eine Leggings kennt,wodurch der Po noch viel mehr in Szene gesetzt wird?

Z.b mit einer raffung zwischen den Pobacken haha

und wie findet ihr gymshark,lululemon und bumbum?

sind die leggins von gymshark Zb echt besser als Zb die von Nike etc?

Hallo. Stimmt es, dass man erst etwas richtig von der Oberweite sieht wenn man ca. >= Einen BMI von 20 hat? Bin 17, 177 groß und wiege ca.57-58 kg und leide sehr unter meiner Oberweite

Hab einen schlanken trainierten Körper, wäre aber gern weiblicher. Was hilft? Bestimmte Ernährung? Oder mehr Fitness? Bitte keine Kommentare wir "akzeptier dich so wie du bist" das tu ich ja. Will lediglich für mich selber was ändern. PS. In meiner Familie haben alle Recht große Oberweite v.a meine Mum

Eine stark absenkende Kurve von 17 Uhr bis 20 Uhr ist bei den Mädchen, die lernen ,zusehen. Ist es richtig beschrieben ?

Wie kommt es, dass Afrikanerinnen, Latinas und teilweise auch Südländerinnen (Italienerinnen, Spanierinnen) von natur aus so kurvig sind? Liegt es an ihrem Lebensstil, an ihrer Ernährung? Ist die Fettverteilung bei denen anders oder machen die alle Bodybuilding? Viele haben breite Hüften und massige Oberschenkel und Popos. (und ich rede wirklich von natürlichen Körpern, nicht wie Shirin David)

https://www.youtube.com/watch?v=hNDXT6hIE8o&t=442s

Wenn ja, wie

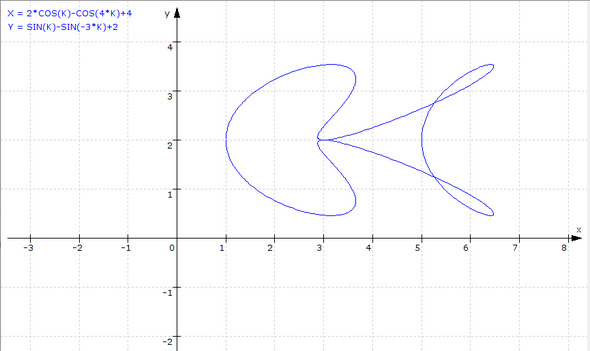
Ich bin auf eine Kurve aufmerksam geworden :

x = 2 * cos(k) - cos(4 * k) + 4

y = sin(k) - sin(- 3 * k) + 2

Wobei k ein Parameter ist, der von - pi bis + pi läuft.

https://www.wolframalpha.com/input/?i=x+%3D+2COS(K)-COS(4K)%2B4+and+y+%3D+SIN(K)-SIN(-3K)%2B2+with+k+from+-pi+to+pi

Hier mal ein schöneres Bild :

Jetzt habe ich mir dazu ein paar Gedanken gemacht :

1.)

Wenn man einen beliebigen Punkt P(x | y) im ersten Quadranten willkürlich wählt, wie kann man mathematisch berechnen, ob der Punkt innerhalb der Fläche liegt, den die geschlossene Kurve einschließt, oder außerhalb der eingeschlossenen Fläche liegt ?

Zum Beispiel ist es für das Auge ganz klar ersichtlich, dass der Punkt (2.5 | 2) innerhalb der eingeschlossenen Fläche liegt, aber der Punkt (2.5 | 4) außerhalb der eingeschlossenen Fläche liegt. Aber wie berechnet man das mathematisch ?

Es kann ja nur 3 Zustände geben : innerhalb der Fläche, außerhalb der Fläche, oder exakt auf der Kurve.

2.)

Wie kann man den Flächeninhalt der Fläche berechnen, den diese Kurve einschließt ?

3.)

Hat diese Fläche eigentlich sowas wie einen Mittelpunkt oder Schwerpunkt ?

Findet ihr meine Figur gut oder nicht so ? Ps: bitte keine unnötigen Beleidigungen

Führerscheinprüfung

kann man durch training und zunehmen wirklich breite hüften bekommen, wenn man von natur aus schmale hüften hat?

Könnt ihr mir sagen, wie ihr das findet.

Nun da ich frisch vom shoppen komme und zahlreiche Tipps und Ratschläge umgesetzt habe (Noch nicht ganz perfekt). Wollte ich nochmal eine Umfrage starten. Wie gefällt euch Damen den der "Zweite Versuch"?

Rat, Tipps und Tricks nehme ich gerne an.

hallo ich hatte heute überlandfahrt und habe es eigentlich auch gut hinbekommen aber bei 2 kurven bin ich viel zu schnell gefahren und hätte die kurven fast bei 90 km/h geschnitten. jetzt wollte ich fragen wie man kurven besser einschätzen kann weil ich habe davor sehr respekt

Nunja, meine Frage ist, wieso ich (w/13) nie angesprochen werde. Ein Beispiel: Ich gehe oft ins Freibad mit eine meiner besten Freundinnen. Auch letzte Woche. Dort war eine Gruppe Jungs, in meinem Alter, vllt 14 oder 15. Mir ist aufgefallen, wie mir zwei der Jungs die ganze Zeit hinterhergeschaut haben, so dass ich es wirklich extrem mitbekommen habe. Allerdings muss ich sagen, dass ich für mein Alter schon wirklich reif bin, geistlich, ziemlich große Brüste und Kurven, vorallem hinten habe, ohne, dass ich damit prahlen will oder arrogant wirken will. Nun hab ich aber nicht das hübscheste Gesicht und werde oft auf meinen Körper reduziert. An meinem Charakter kann es auch nicht liegen. In der Schule bekomme ich das auch stark mit, dass mir auf den Körper geguckt wird und manchmal rufen mir in der Öffentlichkeit irgendwelche Möchtegern-Rambos auch etwas hinterher, wie "Geiler Arsch". Ich möchte nicht zwingend einen Freund haben, aber hätte schon gerne eine Beziehung.

Frage an euch Jungs: Reduziert ihr immer nur auf Asch oder Ttten (sorry, für diesen Ausdruck)? Traut ihr euch nur nicht uns anzusprechen? Wollt ihr von uns Mädchen angesprochen werden, und wenn ja, wie sollen wir euch ansprechen?

Morgen gehe ich mit einer Freundin wieder ins Freibad, ich würde mich freuen wenn ihr mir ein paar Ratschläge geben könntet :)

Schonmal Danke für hilfreiche Antworten :)

Ich bin sehr kurvig gebaut aber wenn ich schwarze Hosen trage sieht man die kurvige Hüfte garnicht mehr . Wird es unter schwarzer Kleidung versteckt ? Auch wenn ich mich komplett schwarz anziehe sieht man nicht mehr , dass ich eine schmale taillie und kurvige Hüften habe . Wenn ich eine helle Jeans und ein helles top anziehe jedoch schon .

Kann es sein , dass schwarz die Kurven verschluckt ?

Hy ich bin ein TransMädchen leider meinen weg noch nicht begonnen weil sich meine mum in meinen weg stellt und bin 14.

Ich habe leider schon echt breite Schultern dafür aber nicht etwas weiblichen Po was mich auch n bissl aufheitern aber jetzt zu meiner Frage

Was kann ich ohne Hormone für eine weiblichere Taille und so machen.

Hbe in den letzten 5 Wochen zwar 8 kg abgenommen aber meine Taille zb ändert sich gar nicht und ich wär einfach jetzt schon gerne viel weiblicher könnte mich mit 11 wegen meiner mum einfach nicht outen weil mir ihre Reaktion klar war und jetzt sehe ich so aus 😭und habe ne tiefe Stimme. 😑

Hey Leute ich möchte mal eure Meinung hören

ich bin ein südländisches Mädchen, ich habe große Brüste, eine schmale Taille/ Breite Hüften aber dafür einen großen Po und etwas kräftige Oberschenkeln. Nebenbei machen ich auch sehr viel Sport zuhause, also ich bin eher kurvig

so Leute ich möchte mal eure Meinung hören wie findet ihr so eine Art Figur, es ist nicht so das ich unzufrieden bin mit meiner Figur, das einzige was mich nur stört sind meine Oberschenkeln aber ich arbeite dran.

Ps: bitte keine blöden Kommentare

lg Dilara

Bin am verzweifeln. Meine Figur geht wie ein strich runter. Keine einzige Kurve. Nichts. Jetzt wollt ich fragen ob man sowas trainieren kann. Ich möchte weiblicher aussehen und nicht mehr so kindlich. Oder werde ich nie si aussehen können?

Hallöchen
Ich bin ein Mädchen (16 Jahre) und hätte mal ne frage an die Jungs hier.
Ich bin 1.67cm groß und wiege zur Zeit 60kg. Ich empfinde das nicht als viel aber auch nicht als wenig. Habe halt etwas mehr an den Oberschenkel aber dafür auch nen großes Hintern😅
Meine Frage ist : steht ihr eher auf dünne / schlanke Mädels oder welche die etwas an sich haben. Und warum ? Ich weiß dass das immer auf den Geschmack ankommt aber würde gerne mal ein paar Meinungen hören :)
LG

Hallo,

Weiss jmd wie man auf die Definitionsbereiche für t (a. bis c.) kommt und wie c) überhaupt geht?

Aufgabe: Parametrisieren Sie die angegebenen Kurven, d.h. geben Sie Funktionen x(t), y(t) sowie den Definitionsbereich für t an, so dass das Bild der Zuordnung

der angegebenen Kurve entspricht. 

a) Die Strecke von P(−3|2) zu Q(15|29). 

b) Die Gerade durch R(8|8) und S(−2|38).

c) Eine (beliebige) Kurve durch die Punkte A(−1| − 5), B(1|3) und C(3|19). (Hier gibt es unendlich viele mögliche Kurven.)  (keine Ahnung wie die Aufgabe geht...)

Hallo, es geht jetzt um eine Frage bzgl. des Parkens in einem verkehrsberuhigten Bereich.
Wir haben einen Nachbarn, der sein Wohnmobil 12 Monate im Jahr, vor der Haustüre stehen hat. (Das Wohnmobil ist ursprünglich ein Lkw gewesen, also richtig groß). Zur Hälfte steht er mit dem Gefährt auf seinem Grundstück, zur anderen Hälfte auf der Straße. Kurz dahinter ist eine Kurve. Das heißt jedes Mal wenn mir ein anderes Auto entgegen kommt, hat man ein Problem und muss wirklich weit zurück fahren, weil man sonst nicht aneinander vorbei kommt. Zusätzlich sieht man wirklich kein bisschen, wenn das Auto des anderen Nachbarn in seiner Einfahrt steht. Durch das Wohnmobil kann man dann auch nicht vor der Kurve ausholen um zu sehen ob da was kommt oder nicht. Außerdem kommen oftmals hinter dem Wohnmobil Fahrräder raus weil dort ein weg endet, die sieht man natürlich auch nicht kommen weil das Riesen Ding dort steht. Das stört wirklich sehr und ich finde es auch gefährlich. Wenn die Müllabfuhr kommt, ist es wirklich cm Sache und sie müssen wirklich gut Rückwärts rangieren.
Jetzt zu meiner Frage: darf er da so stehen ? Ich würde wirklich gerne mal das Ordnungsamt anrufen. Aber vorher möchte ich natürlich gerne wissen ob er das darf.
PS: zwei Nachbarn haben sich schon bei ihm beschwert und gefragt, ob er sich nicht einen Stellplatz suchen kann wie jeder andere Wohnmobilbesitzer auch. Darauf hat er sich aber nicht eingelassen und die Türe vor der Nase zugeknallt. Also er ist wirklich total unkooperativ.

Hey ihr :)

Meine Frage ist ein bisschen eigenartig, aber ich würde gern mal euren Rat hören. Ich bin ein Mädchen und 16 1/2 Jahre alt. Ich sag's mal so, ich hab mich selbst noch nicht so recht gefunden und zweifle oft an mir selbst und hab auch ein bisschen Probleme, meinen Körper anzunehmen und mich zu mögen. Deshalb wollte ich euch mal fragen, wie man eurer Meinung nach als Mädchen in dem alter aussehen sollte? Also damit meine ich zum Beispiel, welche Kleidung man tragen sollte. Mir ist schon klar, dass man das tragen sollte, worin man sich wohl fühlt, ich möchte aber eure Meinung hören.

Und welche Figur ist eurer Meinung nach "normal" in dem Alter? Ich vergleiche mich nämlich oft mit anderen, häufig auch Mädchen, die 2/3 Jahre jünger sind. Da ist man ja häufig noch ein bisschen schmaler und flacher.

Findet ihr es schön, wenn man mit 16 Kurven hat? Also ich meine, wenn die Beine nicht so dünn sind, dass man ne Thigh gap hat oder wenn der Po trainiert und deshalb ein bisschen runder ist?

Mir ist das Aussehen eigentlich nicht so wichtig, aber ich würde gern mal von euch wissen, was ihr in dem Alter "normaler"/"schöner" findet, schon eher wie eine Frau auszusehen oder eher noch wie ein Mädchen mit 13/14.

Liebe Grüße, Engelleinchen!

Also ich bin 1.55 cm Groß,wiege 41 Kg und möchte wissen wie man Kurven bekommt.Ich weiß ich bin noch Jung und so aber ich hasse es ,dass alle das ich ein Stock bin und keinen Arsch habe .-. Muss man viel Sport machen und Proteine und Eiweiße zu sich nehmen? Und wie lange dauert das bis man Kurven bekommt ?

Danke schon mal :)

Hey,

Im Motorsport wird ja vor der Kurve so spät wie möglich abgebremst. Lässt man sich dann in der Kurve durch Rollen und beschleunigt nach der Kurve nochmal richtig durch, oder bremst man stark ab und beschleunigt danach direkt wieder auch wenn man selber noch in der Kurve ist?

Wenn man in der Kurve Gas gibt, hat man ja das Gewicht an den Seiten und vor allem Hinten und somit kann hinten eigentlich bei genug grib nicht ausbrechen oder?

Was ist eurer Meinung nach eine kurvige Frau? Und was zählt für euch schon als "dick" "pummelig" ? Und auf was steht ihr so? Steht ihr auf Frauen mit Kurven ( kurven sind meiner Meinung nach Frauen die etwas pummeliger sind zb mehr am bauch und auf den hüften haben, aber tzd noch eine Taille und auch einen größeren po haben (zb) aber halt alles etwas straffer ansitzt und nicht so viel "rumschabbelt" ) oder steht ihr ehrer auf dünne frauen?

Hallo, ich gebe Mathenachhilfe und mein Nachhifleschüler behandelt zur Zeit Kurvendiskussionen. Sie haben dabei auch die "Lineartermform" und das "Vorzeichendiagramm" benutzt. Kann mir jemand sagen, was es damit auf sich hat? Ich habe von beidem noch nie vorher gehört und im Netzt findet man dazu eigentlich nichts außer ein dreißig-minütiges Video zum VZD. Viele Grüße

Also es passiert oft, dass ich beim Abbiegen also schon am Anfang der Kurve zu schnell bin. Hab zwar den zweiten Gang drin aber was genau soll ich denn machen, wenn ich merke es ist zu schnell? Kupplung drücken ja nicht oder?

Also ich schreibe morgen eine Klausur in Biologie und in dieser müssen wir auch diverse Diagramme und Kurven Interpretieren. Welche Kurven-Typen gibt es da alles ? Ich kenne nur die Sättigungs- und Optimumskurve :/

Hab mit schon sämtliche online Anleitungen durchgelesen aber habe es immer noch nicht so ganz verinnerlicht. Wäre dankbar wenn mir jemand anhand von den eingeramten Beispielen erklären würde was ich machen muss.

Brauche doch den Scheitelpunkt oder nicht? Aber habe doch keine ax^2 + bx + c Form. Wie soll ich den dann herausfinden?

1.) c,d,e

Von der 2.) a,b,c,g

Mit freundlichen Grüßen

Bg13

Hey alle zusammen!! Ich komme bei dieser Aufgabe nicht weiter... :( und zwar verstehe ich nicht inwiefern und wie ich das abschätzen soll... wäre cool wenn jemand von euch weiß wie man das löst... vielen Dank!!! :D

Nach starken Regenfällen im Gebirge steigt der Wasserspiegel in einem Stausee an. Die in den ersten 24 Stunden nach den Regenfällen festgestellte Zuflussgeschwindigkeit kann näherungsweise durch die Funktion f mit f (t) = 0,25t^3-12t^2+144t beschrieben werden (t in Stunden, f (t) in m^3/h).

Aufgabe: Schätzen Sie ab, wie viel Wasser in den ersten 24 Stunden in den Stausee fließt.

Wie kriegt man schöne, runde Kurven? Ich habe Kurven von Natur aus, aber ich würde gerne schönere Kurven haben.

Welche Verschiedenen Kurventypen gibt es in der Biologie? Ich kenne die Optimums- und Sättigungskurve aber da gibt es bestimmt noch mehr oder?

Ich fahre jetz schon seit einem Jahr Motorrad und hatte schon einige kleinere Unfälle mit meiner Enduro. Seit ich davon gelesen habe das ein Motorradunfall in einem Trauma münden kann rede ich mir seit knapp drei Wochen bei jedem kleinen wegrutschet ein das ich Angst vor der Kurve hab und nicht mehr fahren kann. Ich liebe mein Hobby und will es nicht aufgeben jedoch habe ich seit diesem Vorfall immer Angst zu fahren. Kennt ihr das Gefühl ? Habt ihr Tipps oder Erfahrungen gemacht ? Ist es normal das man kurz nach einem wegrutscher Zeit braucht um wieder sicher zu werden ?

LG, Antoni

Hallo. Ich weiß diese Fragen bin ich zu dick? Ist meine Figur normal? Etc. werden oft gestellt. Allerdings bin ich mir bei meiner Figur unsicher, weil meine Freunde und einige Familienmitglieder sagen dass meine Figur normal ist bzw. dass ich schöne Kurven habe,aber mein BMI zeigt an ddass ich leichtes Übergewicht habe. Ich bin 15, weiblich, bin 151 cm klein wiege 60 kg. Meine Maße : Brust 95cm, Taille 74cm, Po/Hüfte 102cm Ich persönlich mag meinen Bauch, meine Oberarme und meine Oberschenkel nicht so sehr. Mit meiner Brust und meinem Po bin ich eigentlich ziemlich glücklich. Dazu muss ich sagen, dass ich mich gesund ernähre und 3-4 mal die Woche Sport mache. (Workouts)Außerdem bin ich fast immer den ganzen Tag unterwegs. Also was meint ihr? Bin ich zu dick, normal oder habe ich eine schöne kurvige Figur? Denn unter Kurvig wird oft entweder fett bzw. dick oder schlanker Bauch, schlanke Beine etc. aber großer Po und große Brüste verstanden.

Hey also ich wollte fragen ob ich mit dem Moped in der Kurve hochschalten kann ohne mich abzulegen? Ich "kann" Kurven fahren. Ich möchte nur manchmal mit mehr Geschwindigkeiten raus aber ich weiß auch das runterschalten schief geht (meistens) aber zu hochschalten weiß ich nichts. Bitte helfen.

Wieso sind für fast alle Motorradfahrer linkskurven leichter als rechts, obwohl man rechtshänder ist???

Hallo Liebe Community, da ich meinen Führerschein im Ausland gemacht habe habe ich das nie gelernt und zwar: in meiner Region hier gibt es viele sehr steile strecken. (Gefühlt 45%) Beim hochfahren ist's ja klar, da bleibt man in tiefen Gängen auf hohen Drehzahlen damit man trotz dem beschleunigen kann; die großen Gänge schaffen das ja nicht. Aber beim runter fahren, ist es da schlecht beispielsweise bei 100 im 3 Gang zu schleifen oder machen die hohen Drehzahlen den Motor kaputt? Im Grunde gebe ich ja nie Gas desshalb ist der Sprit Verbrauch ja nicht vorhanden. Ich würde jedoch lieber die motorbrmse nutzen als konstant auf der Bremse zu hängen, die kann in der Zeit ja nicht mal abkühlen da es eine sehr steile kurvige Strecke ist.
Danke für eure Antworten
Ifrit

Frage an die Boys
Steht ihr eher auf so magere Girls oder auf Mädchen/Frauen mit paar Kurven.
Meinungen?

Ich habe mal ne Frage die hört sich zwar bescheuert an aber egal 😂😂.Habt ihr Tipps wie man einen Po bekommt der nicht so meega knochig ist also einen po der so ein bisschen schwabbelt (beim Twerken ) und einen Geoßen ? Falls ihr wisst ,was ich meine

Ich fahre eine Supersportler und habe gehört dass man in den Kurven den Hintern, also die eine Backe des Hinters, vom sitz hängen lassen soll und sich dann in die kurve legen soll.

Bislang habe ich das aber noch nicht wirklich probiert und lege mich einfach ganz normal in den kurven, allerdings hatte ich jetzt schon des öfteren in scharfen Kurven das problem das ich kurz mit der fußraste aufsetze. Hat man durch das raushängen der backe mehr reserve für die kurve oder warum soll man das machen?

Hey zusammen, Ich bin 17 jahre alt und hab fast gar keine Kurven woher viele meinen das ich viel jünger aussehe als ich bin Habt ihr tipps? Oder Trainingsübungen? Was soll ich machen? Dankeschön schon mal im Vorraus

Ich habe mein Handy auf dem Autodach vergessen und bin von der Ortschaft rausgefahren. Da ich eher langsam unterwegs war ist es lange nicht runtergefallen. Aber als ich dann schneller unterwegs war und mit 80 - 100 kmh eine leichte Kurve nach rechts gefahren (+wurde Steil) bin habe ich gehört wie es runtergeflogen ist. Habe angehalten aber weder rechts noch links nichts gefunden. Auch nach der Handy-ortung konnte ich es nicht finden (lautlos).

Also meine Frage ist in welche Richtung könnte es eher geflogen sein? Hatte es auf der Fahrerseite. Mein Handy hatte eine plastik Handyhülle. Und wie weit kann es bei dieser Geschwindigkeit fliegen?

Hey könnt ihr mir helfen, Hafensänger? Ich habe ein Bild und brauche eine Funktion die sich derer im Bild annähert. Es handelt sich um ein Bierglas

Ich möchte anfangen zu trainieren um meinen Traumkörper zu kriegen. Ich habe schon kurven, nur wollte ich wissen, ob ich mit bestimmten übungen sie noch kurviger kriege ? Falls ja, könntet ihr mir auch welche Vorschlagen? Meine andere Frage wäre, ob falls ich meinen Hintern anfange zu trainieren , er schmaller wird ? Ich habe schon einen breiten und recht grossen Po, ich will ihn nur runder kriegen, aber will halt nicht das er schmaller bzw kleiner wird. Schonmal danke im vorraus (-:

Hey Also man erkennt ja Hoch- Tiefpunkte mit der 2. Ableitung, oder mit dem VZW, durch die Vorzeichen. Aber wenn erkenn ich, dass es z.B gar kein Wende- sondern Sattelpunkt ist. Ich weiß nur, dass wenn man eine 3-fache Nullstelle hat, dass es ein Sattelpunkt ist (x³). Und wie noch?

Ich habe leider vieles, wegen meiner OP verpasst. Kann mir jemand die Eigenschaften und die Unterschiede zwischen dieser und der normalen Sinus Kurve nennen? Und woher man das wissen kann.
Bitte aufrichtig um Verständnis und Hilfe.
Gruß.

Hallo, diese Frage ist jetzt etwas dumm aber ich wollte wissen ob und wie man den Körper (Bild) bis zum Juni 2017 bekommen kann, wenn ich hart genug dafür arbeite. Ich bin 161 cm, 13 Jahre alt, wiege 47-52 Kilo und mein Oberkörper ist 81-65-81cm. Das Bild hab ich von Instagram, und ich weiß das es auch bearbeitet sein könnte, aber das stört mich nicht.

Hallo.. Also ich bin 14 und Araberin. Alle meine arabischen Freundinnen haben voll den großen a$$ und voll die schönen Kurven.. Ja, anscheinend haben das alle arabischen Mädchen außer ich.. Ich hab mich gefragt ob man durch bestimme Sportarten (wenn ja, welche?) Kurven bekommen kann? Zum Beispiel einen großen Ar$ch, größere Hüften, und das eine Ding bei der Taille, das so reingeht (ka wie man das nennt hahaha) oder ist das einfach angeboren und lässt sich nicht ändern? Ich weiß, dass man 'nen größeren Po durch Kniebeugen bekommen kann, aber kann man auch irgendwie seine Hüften durch Sport runder machen? Weil meine gehen irgendwie nicht nach außen, sondern nach innen, ich weiß nicht, wie man das erklären kann und das schaut so mega scheißee aus. Und das größte Problem ich kann auch irgendwie nicht zunehmen und bin einfach so dünn wie ein Stock. Wie kann ich das ändern?

Danke schon mal im Voraus für alle Antworten :)

Ich habe das Problem, dass mir die Kurven (Vektorgrafik), die ich in Affinity-Designer erstellt habe, immer noch als sehr "eckig" erscheinen. Gibt es da eine Möglichkeit, diese Kurve ausgewogen rund hinzubekommen? Auf "Glatte Kurve" klicken bringt überhaupt nichts; das wird noch eckiger.

Danke für eure Antworten!

Finden Männer (oder Frauen)es geil brüste anzufassen und wenn ja wieso?

Ich bin weiblich und 13 ich habe überhaupt keine Kurven ich habe keine Brust keinen Po und alle meine Freundinnen haben viel mehr ich habe noch nicht mal eine richtige Körbchengröße trage aber trotzdem frische Fische ob er einen Push Up BH A ich weiß ich werde auch nie viel Kuchen bekommen da meine Mutter auch nur Körbchengröße A hat wisst ihr ob das normal ist und es noch kommen kann oder was man dagegen tun kann

Hallo, ich habe so eine mega schwachsinnige Frage undzwar, wenn man Kursagen trägt (oder wie man das schreibt) trägt, dann kriegt mann ja schöne weibliche Kurven.. Kriegt man diese aber dann nicht auch, wenn man den eigenen Gürtel (von einer Hose) sehr straff trägt? Also so sehr eng und nicht nur so ,,normal"? Weiß das jemand? Weil das ist ja doch so ähnlich oder nicht? Danke für die antworten.

Bei nur ungeraden exponenten ist es eine punktsymmtrie und bei nur geraden exponenten eine achsensymmetrie. Gilt diese regel auch bei negativen exponenten, zum beispiel ist der exponent ,, (-2) " dann ist das gerade aber eine negativer exponent

Hallo,
Ich habe mich folgende Frage gefragt, brauchen Mädchen im Alter von 13-15 Jahren Kurven?

Ich bin 13 Jahre alt, ziemlich dünn, habe einen kleinen Po und somit keine Kurven.
Bei meiner Mutter sieht das alles nicht anders aus, bis auf das sie ein schlankes Normalgewicht hat.
Somit liegen meine Chancen auf schöne Kurven und einen normal/großen Po niedrig.

In meiner Klasse und meinem Freundeskreis werde ich als Stock ohne Asch und Kurven dargestellt!

Was sagt ihr dazu und hattet ihr das selbe Problem, habt aber durch Übungen oder Natur einen schönen "großen" Po bekommen?

Hallo liebe Community, wie haben folgene Aufgabe: die Wasserrutsche am Kinderbecken ist etwas in die Haare gekommen. Sie soll durch eine Rutsche mit dem graphischen Design eines Polynom 3. Grades ersetzt werden: die Rutsche schließt in C und B knickfrei an die waargerechten Stücke an. der Boden der Rutsche AB: 4m der kleine Rutschteil über dem Wasser: 0.5m vom boden zum Startpunkt der Rutsche: 2m Brauche nur Holfe Hilfe bei den Bedingungen. Danke schon einmal im Voraus!

was ist kurve schneiden

Hallo Leute. Ich wollte euch mal fragen wie ihr bei GTA 5 scharfe Kurven richtig nehmt, bremst ihr am Anfang oder gar nicht oder sonstiges? Schaffe die Kurven meistens nicht und hoffe deswegen auf eure Hilfe. (Spiele auf PC)