Problemstellungen bezüglich geschlossenen Kurven in Parameterdarstellung (Parameterkurven)?
Ich bin auf eine Kurve aufmerksam geworden :
x = 2 * cos(k) - cos(4 * k) + 4
y = sin(k) - sin(- 3 * k) + 2
Wobei k ein Parameter ist, der von - pi bis + pi läuft.
Hier mal ein schöneres Bild :
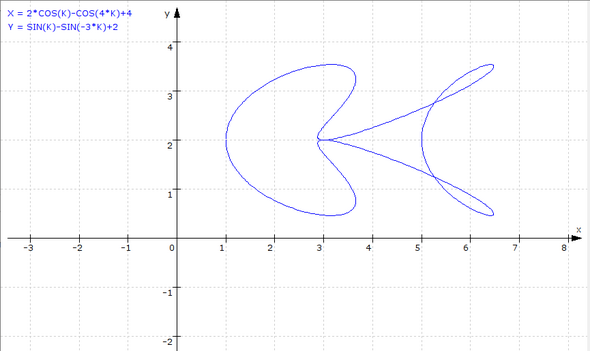
Jetzt habe ich mir dazu ein paar Gedanken gemacht :
1.)
Wenn man einen beliebigen Punkt P(x | y) im ersten Quadranten willkürlich wählt, wie kann man mathematisch berechnen, ob der Punkt innerhalb der Fläche liegt, den die geschlossene Kurve einschließt, oder außerhalb der eingeschlossenen Fläche liegt ?
Zum Beispiel ist es für das Auge ganz klar ersichtlich, dass der Punkt (2.5 | 2) innerhalb der eingeschlossenen Fläche liegt, aber der Punkt (2.5 | 4) außerhalb der eingeschlossenen Fläche liegt. Aber wie berechnet man das mathematisch ?
Es kann ja nur 3 Zustände geben : innerhalb der Fläche, außerhalb der Fläche, oder exakt auf der Kurve.
2.)
Wie kann man den Flächeninhalt der Fläche berechnen, den diese Kurve einschließt ?
3.)
Hat diese Fläche eigentlich sowas wie einen Mittelpunkt oder Schwerpunkt ?
2 Antworten
Vorneweg: Deine Kurve ist ein besonders schönes Exemplar einer Lissajous-Figur. Möglicherweise findest Du zu diesem Thema eine Veröffentlichung, die alle Deine Fragen beantwortet.
Es kann ja nur 3 Zustände geben
Deine 3 Zustände innen/außen/Rand gibt es nur bei geschlossenen Jordan-Kurven. Ansonsten sieht es bitter aus.
kann man mathematisch berechnen, ob der Punkt innerhalb der Fläche liegt
Bei einer konvexen, fast überall differenzierbaren Kurve x(t) ist das einfach: Berechne die Kurvennormale n(t) und teste dann, ob P immer auf der gleichen Seite der Tangente liegt. (Ich gehe davon aus, dass Du weißt, wie man die Tangente berechnet und mit der Hesseschen Normalform vertraut bist. Falls nicht, wirst Du ab jetzt nur "Bahnhof" verstehen.)
Läuft die Kurve gegen den Uhrzeigersinn, heißt das:
P liegt innen ⇔ ∀t: n(t)·P > n(t)·x(t).
(Bei Orientierung im Uhrzeigersinn vertauscht sich "innen" und "außen". Dann drehe oben einfach das Kleiner-Zeichen um.)
Sobald die Kurve "Dellen" hat, klappt das aber nicht mehr. Hier könntest Du z.B. erst einen festen Punkt P₀ wählen, von dem Du weißt, wo er liegt. Nun bestimmst Du alle Schnittpunkte der Strecke P₀P mit der Kurve x. Bei jedem Schnittpunkt wechselt die Strecke von "innen" nach "außen" oder umgekehrt. Ergo:
P liegt auf derselben Seite wie P₀ ⇔ | P₀P∩x | ist gerade.
Möglicherweise gibt es auch effizientere Verfahren (vgl. Jordan-Test). Super wäre es natürlich, wenn Du eine stetige Abbildung im ℝ² findest, die Deine Kurve konvex macht. Das gleicht aber wohl der Suche nach der Nadel im Heuhaufen.
Enthält die Kurve Doppelpunkte (=Schnittpunkte mit sich selbst), ist nicht einmal mehr klar, was "innen" und "außen" sein soll. Bei Deiner Kurve sind die beiden "Schwanzflossen" rechts gemeint: Zählen sie als "innen"? Dann müsstest Du die Kurve an ihren Doppelpunkten in mehrere Einzelkurven zerlegen. Ein Punkt liegt dann "innen", wenn er innerhalb (mindestens) einer Einzelkurve liegt. "Mindestens" deshalb, weil Du auch Überlappungen haben kannst: Male z.B. eine nicht ganz perfekte 8 ("oO") und klappe den kleineren Kringel in den großen hinein. Was ist hier innen und außen?
Wie kann man den Flächeninhalt der Fläche berechnen
Das ist ziemlich einfach: Bei einem Polygon nimmst Du einen beliebigen Punkt S im Innern und addierst dann die (orientierten) Flächen der Dreiecke zu allen Seiten. Das klappt auch, wenn S außerhalb des Polygons liegt, und sogar dann, wenn das Polygon nicht konvex ist: Mit den orientierten Flächen wird dann an manchen Stellen zu viel berechnet, was an anderen Stellen dann wieder abgezogen wird. In Summe passt's aber.
Bei einer differenzierbaren Kurve werden die Polygonseiten zu infinitesimalen Tangenten und aus der Summe wird ein Integral. Effektiv landest Du dann bei der Formel F=½∫ n(t)·x(t) dt (zumindest, wenn x(t) in Bogenlänge gegeben ist).
Aber Vorsicht bei Doppelpunkten: Teilflächen mit negativem Umlaufsinn haben auch eine negative Fläche. Hier muss das Integral wieder für jede Jordan-Kurve getrennt berechnet werden. Und bei der oben erwähnten "eingeklappten 8" würde der innere Kreis doppelt zählen. Solche Fälle können einem das Leben richtig schwer machen.
Hat diese Fläche eigentlich sowas wie einen Mittelpunkt oder Schwerpunkt ?
Jede beschränkte Fläche hat wohl einen Schwerpunkt. Allerdings hängt das auch hier massiv von der Definition für innen/außen ab. Man muss hier wieder aufpassen, dass man nicht einige Teilflächen mehrfach oder negativ bewertet.
Für Polygone ohne Doppelpunkte gibt es eine einfache Formel für den Schwerpunkt, aber schon bei einem Kreisbogen muss man sich offenbar mit einer Näherung zufrieden geben. Eine differenzierbare Jordankurve kannst Du aber auf jeden Fall durch Polygone annähern und damit ungefähr ihren Schwerpunkt bestimmen. Für eine exakte Berechnung müsstest Du die Polygonsummen durch Grenzübergang in ein Integral verwandeln; allerdings bezweifle ich stark, dass das Integral bei Deiner Kurve geschlossen lösbar ist.
Bei mehreren Jordan-Kurven berechnest Du jeden Schwerpunkt einzeln und bildest dann das mit seiner Fläche gewichtete Mittel.
Nur mal ein paar Gedanken, ohne selbst Mathe-Freak zu sein
zu 1) innerhalb der Kurve bedeutet, dass es sowohl rechts und links sowie oben und unten ein (x,y) gibt (wobei eigentlich noch zusätzlich zu prüfen wäre, ob die Figur um den Punkt geschlossen ist). Die Prüfung, ob rechts, links sowie oben und unten von dem Punkt ein (x,y) kann man wohl einfach per Gleichung herausfinden.
Die Prüfung, ob und wo die Kurve sich schließt, läuft wohl per Kurvendiskussion, also herausfinden, wo die Kurve von verschiedenen Richtungen zusammenläuft, also wo die Kurve nicht injektiv ist, wo sie nicht surjetiv ist, dasselbe für die "Umkehrfunktion", also Betrachtung von injektiv und surjetiv nach x,y-Vertauschung. Wenn man die Punkte hat, an welchen die Kurven nicht mehr Injektiv oder nicht mehr surjetiv werden, kann man natürlich auch sagen, ob der Punkt "in" der Figur ist.
zu 2) Fläche: Das wäre mich zu hoch. Ich würde Abschnitte bilden, daraus Funktionen ableiten und dann die Integrale ausrechnen.
zu 3) der Schwerpunkt ergäbe sich aus der Fläche. Da die Figur symmetrisch zu y=2 ist, muss man nur auf y=2 dasjenige x finden, bei welchem die Fläche rechts von x = Fläche links von x ist. Der Mittelpunkt ergibt sich leicht aus den x- und y-Längen.
Aber warte einfach nochmal einen Tag ab, bis sich die Mathe-Freaks auf GF gemeldet haben.
Ok, Danke für deine Antwort !
Ich werde mal drüber nachdenken.