Ich muss einen Argumentativen Text über Homeschooling schreiben habe auch einige Gute Punkte gefunden Für Homeschooling und gegen aber ich weiß nicht wie ich das in einem Text verfasse.
Habt ihr eine Idee?
These:Homeschooling ist eine Alternative zu realen Schule.
• Einige Lehrer Antworten nicht auf deine E-Mails
• Manche Schüler nehmen das Konzept nicht Ernst
• Im Homeschooling kriegt man manchmal viel zu viele Aufgaben
• Kann nicht direkt Fragen stelle und eine Antwort kriegen. Meist ist man schon mit was Komplet anderem beschäftigt
• Organisation ist schlecht (meinst nur bei nicht Digitalen Schulen)
• Man kann sich schnell ablenken lassen
• In der Schule gibt es einen Vorgeschriebenen Stundenplan damit lernt man viel mehr in kürzester zeit
• Zeit schlecht einteilen
• Von jedem Lehrer Aufgaben in der Schule
• Man muss sich einige Themen selbst aneignen
• Man sieht Mitschüler, Freunde und Lehrer
• Beim Besprechen von Aufgaben in der Schule fällt direkt auf wenn du die Aufgabe nicht hast
• Es gibt Kein besprechen von Aufgaben das bedeutet man kann die Aufgaben auch mal einen Tag später erledigen
• Kannst in bequemer Kleidung jeder Art rumlaufen
• Digitale Schulen haben vorteile:
👉🏻Die Schüler sind mit digitalen arbeiten schon länger vertraut(haben mehr Praxis erfahrung). Besitzen bereits gute Apps wo Aufgaben hingeschickt werden können. Da gab es auch im Unterricht einführung wie man sie benutzt.
👉🏻 Beispiel Onenote: Es gibt bereits Schulen die diese App benutzen und super zufrieden sind. Sogar die Scüler finden die App gut und nutzen sie gerne. Es gibt dort Ordner zum Beispiel Phisik 8.1 und wenn man dann da drauf klickt gibt es noch mehr Ordner zu diesem Fach zum Beispiel Notizen oder einen der ist so Ähnlich wie eine Whatsapp Gruppe. Es kann dort jeder Aus dem Kurz reinschreiben. Bei anderen Ordner Kanst nur du reinschreiben oder reischreiben. Außerdem gibt es ordner wo nur du und der Lehrer Reinschauen und Schreiben kann. Andere Ordner sind Hausaufgaben oder Vokabeln…
👉🏻Wenn man mit Ipads oder Ähnlichen Arbeitet kann man nie etwas vergessen denn du hast fast alles digital. Verloren geht auch weniger. Man hat auch vieles viel schneller grifbereit
• Man kann länger schlafen
• Selber einteilen wann man welches Fach machen möchste
• Spart den Weg zur Schule
• Man lernt eigenständiges Lernen
• Ansteckungsriesiko ist geringer
Ich muss einen Text verfassen.
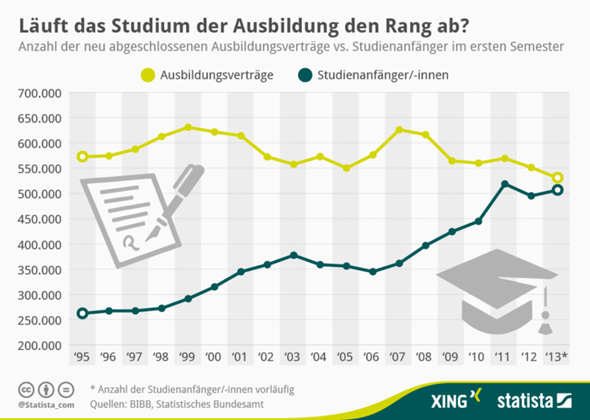
Weiß jemand wie viele Kinder 2020 oder 2019 statistisch im Hausunterricht Sind ?
Danke schon mal im Vorraus.