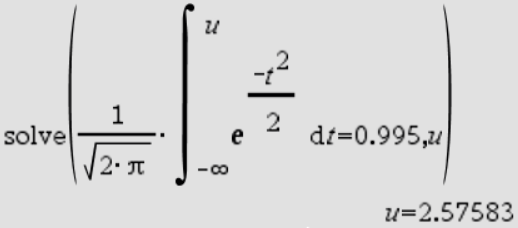Ein Student, der keine Zeit hat, sich auf einen 20-Fragen-Multiple-Choice-Test vorzubereiten, beschließt, bei jeder Frage aufs Geratewohl zu raten. Dabei besitzt jede Frage fünf ¨ Antwortmöglichkeiten, von denen jeweils nur genau eine richtig ist. a) Welche Verteilung hat die Zufallsvariable, die die Anzahl der richtigen Antworten angibt? Wie viele Fragen wird der Student im Mittel richtig beantworten? b) Der Test gilt als bestanden, wenn zehn Fragen richtig beantwortet sind. Wie groß ist die Wahrscheinlichkeit, dass der Student den Test besteht? Wo musste die Bestehens Grenze liegen, wenn die Chance des Studenten, die Klausur durch Raten zu bestehen, großer als 5% (50%) sein soll?
A habe ich verstanden aber Aufgabe B verstehe ich nicht. Lösung: b) Die Wahrscheinlichkeit, den Test zu bestehen: P(X ≥ 10) = 1−P(X < 10) = 1−P(X ≤ 9) = 1−FX(9|20; 0, 2) = 1−0, 9974 = 0, 0026. Die Wahrscheinlichkeit fur ¨ X ≤ 9 wird einer Tabelle entnommen. Die Grenze k, bei welcher die Wahrscheinlichkeit, die Klausur zu bestehen, mehr als 5% betr¨agt, berechnet sich wie folgt. P(X ≥ k) = 1 − P(X < k) > 0, 05. Umformung liefert: ⇐⇒ k = 7. Wenn die Chance der Studenten, die Klausur durch Raten zu bestehen, gr¨oßer als 5% sein soll, muss die Bestehensgrenze bei 7 richtigen Antworten liegen. Zusatz: P(X ≥ k) = 1 − P(X < k) > 0, 50. P(X < k) < 1 − 0, 5 ⇐⇒ k = 4. Die Grenze liegt bei k = 4. Wenn die Chance der Studenten, die Klausur durch Raten zu bestehen, gr¨oßer als 50 % sein soll, muss die Bestehensgrenze bei 4 richtigen Antworten liegen.
Kann mir das jemand erklären?