Formel der Standardabweichung/Varianz?
Die Standardabweichung lässt sie ja berechnen, indem man die Wurzel aus der Varianz zieht. So weit so gut.
Nun ist die Formel, die ich auf diversen Youtube Videos und Seiten finde die folgende:
Man teilt die quadrierten Abstände zum Mittelwert durch die Anzahl der Beobachtungen.
Nun habe ich auf in dem Skript meines Profs die Formel etwas abgeändert stehen. Und zwar teilt er nicht durch die Anzahl der Beochbachtungen, sondern durch die Anzahl der Beobachtungen - 1.
Ich lade die beiden Formeln auch nochmal als Bild hoch, damit es ein wenig anschaulicher wird.
Kann mir irgendjemand erklären, warum mein Prof durch "n-1" und nicht nur durch "n" teilt?

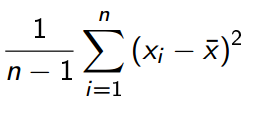
3 Antworten
Die Formel mit n BERECHNET die Varianz der Stichprobe und SCHÄTZT die in der Grundgesamtheit, sofern der Mittelwert dort bekannt ist (was so gut wie nie der Fall ist).
Die Formel mit n-1 SCHÄTZT die Varianz in der Grundgesamtheit aus der Stichprobe, wenn der Mittelwert dort nicht bekannt ist - und also auch geschätzt wird.
Es ist irgendwie einleuchtend, dass die geschätzte Varianz bei unbekanntem Mittelwert etwas größer ist.
Drainage hat übrigens recht mit seiner Aussage über die Erwartungstreue.
Ich kenne auch beide Varianten (wobei die mit n bei weitem häufiger benutzt wird). Auf einem meiner Taschenrechner sind auch beide Formeln hinterlegt.
Grund? Vielleicht soll so "künstlich" bei kleinem Wert von n die Varianz erhöht werden??
Auf jeden Fall ist es mit "n-1" unmöglich, die Varianz bei nur einem Messwert zu berechnen - aber wer will das schon?
Der Grund ist ganz simpel: Weil die naheliegende Formel mit 1/n nicht erwartungstreu ist, die mit 1/(n-1) hingegen schon.
Ich hoffe es und wenn nicht, googelt man mal eben den Wikipediaartikel. So schwierig ist das nicht zu verstehen.
Glaubst Du, dass einer, der die obige Frage stellt, mit Deiner Antwort etwas anfangen kann? Meinst Du, er weiß, was erwartungstreu ist?