Wertepaare Funktionsgleichung aufstellen?
links x, rechts f(x)
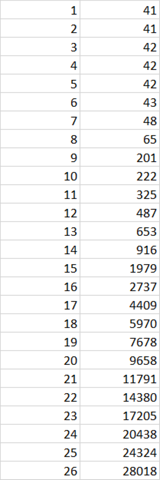
Kann mir jemand eine Funktionsgleichung aufstellen, die der Funktion, auf der die Punkte oben liegen, am nächsten kommt? Wer herausfindet, was das für Daten sind bekommt n Preis.
4 Antworten
Hallo Knochendochen13,
ich vermute, dass es sich bei der Wertetabelle um die Anzahl f der Infizierten des neuen Coronavirus handelt, welche in Abhängigkeit von der Zeit x in Tagen angegeben ist. Daher habe ich die Funktion mal mit Hilfe von folgendem exponentiellen Ansatz gefittet:
f(x) = a * e^(b*x)
Der Anfangsbestand a ist hier mit 41 Infizierten vorgegeben und der Fit ergibt für die Wachstumskonstante b einen Wert von 0,256074 [1/Tag]. Aufgrund einer relativ groß anzunehmenden Fehlertoleranz, die ich bei dieser Beispielrechnung mangels entsprechender Abschätzungen natürlich nicht berücksichtigen kann, sind die vielen Nachkommastellen allerdings eher irreführend als nützlich. Daher runde ich es mal ganz frei auf 0,26 [1/Tag] auf mit dem Hinweis auf eine große Fehlertoleranz, die ggf. bei entsprechend vorhandenen Daten noch zu bestimmen wäre.
Ich habe die Funktion zusammen mit den Werten mal geplottet:
-> https://www.bildhost.com/image/Yak1YJ
Ich hoffe, dass ich dir weiterhelfen konnte. Falls du noch weitere Fragen hast, dann schreibe einfach einen Kommentar! ;-)
Viele Grüße
Julian Schmidt
Danke für die Antwort!
Mit dem Coronavirus liegst du richtig.
Habe die Daten von dieser Webseite: https://wuhanviruslive.com/.
Naja, nachdem ich ein bisschen rumprobiert habe kam ich auf folgende 2 Möglichkeiten:
1: (1)/(990000) (x+2)^(7)+41.5
2: (1)/(990000)x^(8)+41.5
Ich habe hierfür ein Programm programmiert dass (fast) alle Möglichkeiten probiert hat. Das sind gerundete Werte die aber schon ziemlich genau sind. Das Programm rechnet graphisch... die Punkt und die werte sind rel. verscheiden, aber die Funktion schneidet knapp die Punkte (max 1 Einheit)... Ich weiß nicht wofür du die Funktion brauchst, aber ich hoffe ich konnte dir helfen...
Danke für die Mühe, aber die Funktionen sind schon ziemlich ungenau. Bei der ersten Funktionsgleichung ist zum Beispiel f(22)=4674,2994181818.... . Das ist schon ziemlich weit weg von 14.380 wie es sein sollte. Bei der Zweiten Funktionsgleichung ist f(22)=55471.67528888889. Auch ziemlich weit weg. Ich bin gerade darauf gekommen, dass ich die Wertepaare ja auch in Excel eingeben könnte und Excel spuckt mir da f(x) = 0,0011x^6 - 0,0971x^5 + 3,1779x^4 -45,44x^3 + 296,29x^2 - 796,48x + 665, 78 aus.
ich habe erwähnt, dass die werte nicht so übereinstimmen... Der Graph liegt in der nähe der Punkte... er ist sehr steil, sodass nur eine Einheit unterschied bereits 100K unterschied machen kann
Also Excel kann so etwas auch: Die blaue Linie sind deine Punkte. Die Punkte, sowie die Funktion die Annährung die Excel berechnet hat. Dies ist eine Annährung 3ten Grades. Bei Grad 6 ist es noch Deckungsgleicher. Ich tippe auf den Dow Jones Index.
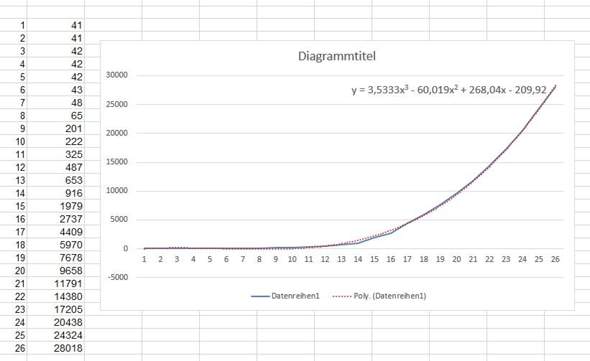
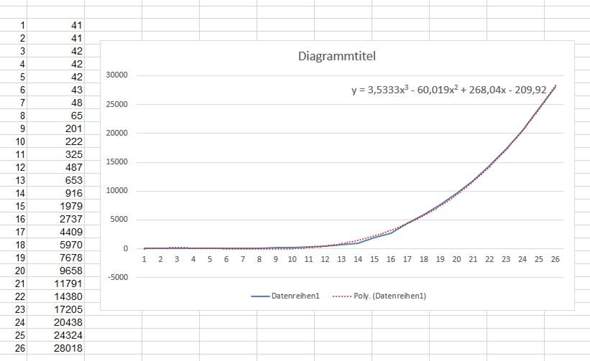
Danke, darauf bin ich auch gerade gekommen. Ich hab mal es mal mit verschiedenen Funktionstypen versucht und das genauste, was er mir ausgespuckt hat, war, wie du sagst, eine Polynomfunktion 6. Grades: f(x) = 0,0011x^6 - 0,0971x^5 + 3,1779x^4 -45,44x^3 + 296,29x^2 - 796,48x + 665, 78.
Sorry typo. DOW Jones. Amerikanischer "Haupt Aktien" Index. Start und Ende stimmen einigermaßen überein (je nach Zeitpunkt) Zwischenwerte habe ich nicht geprüft.
Nein, das ist es nicht. Es sind die Daten für die Zahl der mit dem Coronavirus infizierten Menschen in Abhängigkeit zur Zeit.
Du könntest die Punkte durch ein Polynom interpolieren. Und mit einem Poylnom vom Grad 25 solltest Du alle Punkte exakt treffen können. Mehr dazu findest Du hier:
https://de.wikipedia.org/wiki/Polynominterpolation
Wenn es nicht 100 Prozent exakt sein muss, dann könnte man Regressionsmethoden verwenden. Schon ein Polynom dritten Grades liefert Ergebnisse die sehr nah an Deinen Zahlen sind. Für die exakte Spezfikation siehe hier:
Oder alternativ eine Exponentialfunktion. Siehe hier:
Danke für die Antwort! Habs jetzt mal mit Excel versucht und es kam folgenden Funktion sechsten Grades heraus: f(x) = 0,0011x^6 - 0,0971x^5 + 3,1779x^4 -45,44x^3 + 296,29x^2 - 796,48x + 665, 78.
Diese Webseite spricht vor 26 Tagen von 41 Infizierten: -> https://www.dw.com/de/china-meldet-ersten-todesfall-durch-neue-lungenkrankheit/a-51964291
Diese Webseite spricht von aktuell mehr als 28000 Infizierten: -> https://www.businessinsider.de/international/china-virus-everything-we-know-deadly-2019-ncov-wuhan-spread-2020-1-2/
Dies entspricht sehr gut den Start- und Endwerten deiner Tabelle.