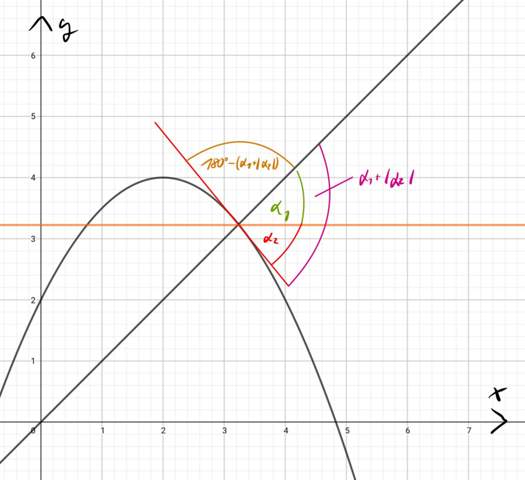
Flächenberechnung aber wieso die Formel?
Ich habe die Aufgabe soweit bearbeitet und auch verstanden aber wo ich einfach nicht drauf komme ist, wie man auf die Formel oder Gleichung der Fläche des Dreiecks in der Mitte kommt, also: „1/2k mal Wurzel k^2 - 1/4 k/2 = Wurzel 3/4 k/2“ ?
Und danach dann noch die Gleichung der blauen Fläche, wie man auf die Gleichung kommt :/
Im Grunde ab „Wichtig“ am Ende komme ich nicht mit bei der Rechnung.
Einmal die Bearbeitung: Gesucht ist der Flächeninhalt der blauen Fläche