Grenzverhalten von zusammengesetzten Funktionen?
Woran erkenne ich anhand dieser Funktion ohne Taschenrechner, ob sie gegen +-unendlich oder gegen 0 verläuft?
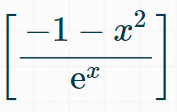
Also bei x-> +∞ verläuft sie gegen 0 und x-> -∞ verläuft sie gegen -∞. Ich verstehe das iwie nicht weil das in Bruch ist.. Wie kommt man drauf
2 Antworten
x gegen unendlich:
Die e-Funktion wächst schneller als jedes Polynom, also geht der Nenner schneller gegen unendlich als der Zähler, der Brich geht also gegen 0.
x gegen -unendlich:
Schreibe es um zu e^-x*(-1-x^2)
Der erste Faktor geht gegen unendlich, der zweite gegen -unendlich, somit geht das Produkt gegen -unendlich.
e^-x geht für x gegen unendlich gegen 0, aber nihct für x gegen -unendlich.
e^x wächst für x gegen unendlich schneller als jede Potenz. Damit sollte eine qualitative Betrachtung des Verhaltens für x gegen +/-unendlich (das ist kein "Grenzwert") kein Problem sein.
e^-x geht doch gegen 0 oder nich hää