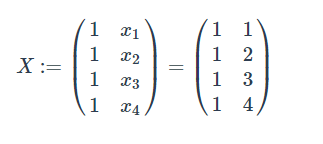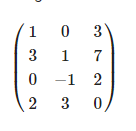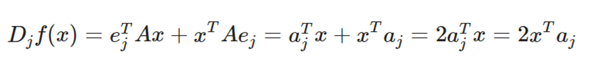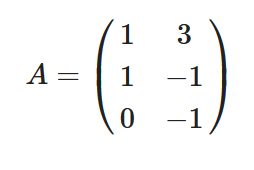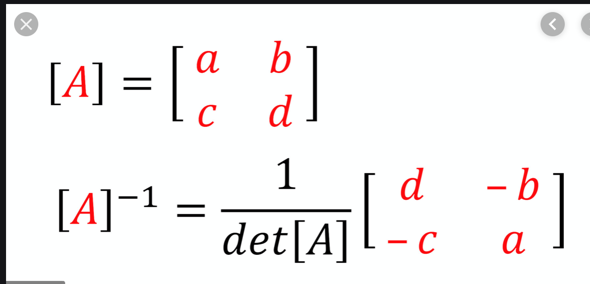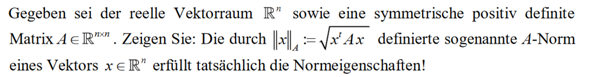Matrix – die neusten Beiträge

Guten Abend liebe Community, ich habe folgendes Problem. Nämlich komme ich bei einer Aufgabe nicht weiter.

Berechnen sie die fehlenden Werte a, b, c, und d

Leslie-Matrix=

0 0 a

b 0 0

0 c d

Gegeben sind Folgende Startwerte: 1200 Eier im ersten Jahr, 250 Larven und 65 Bienen.

Im zweiten Jahr: 780 Eier, 480 Larven und 132 Bienen.

und im 3. Jahre 1584 Eier, 312 Larven und 255.6 Bienen.

Ich soll herausfinden wie viele Bienen aus den Larven entstehen und wie viele Überleben habe aber leider keinen Ahnung wo ich dort ansetzten soll.

Ich bin momentan soweit, dass ich die einzelnen Vektoren der Basis b in die Funktion eingesetzt habe und nun drei Polynome erhalten habe. Ich weiß nun nicht, was ich mit diesen drei Polynomen anfangen soll...

Ich konnte der letzten Übung nicht teilnehmen und mein Partner hat das nicht verstanden. Soweit ich sehen kann, kommt als Ergebnis eine 4x3 Matrix raus. Momentan finde ich nicht heraus, wie man aus den drei Polynomen die vier Einträge einer Spalte erhalten kann.

Hall0!

Angenommen man habe die Matrix der Form

Wie berechnet man davon ausgehend den Spann dieser Matrix?

Danke im Voraus!

2018 hatte ich die meisten Deja vus gehabt, genau diese Situationen muss ich mit 4 Jahren geträumt haben.

Jeder Mensch hat Deja vu Erlebnisse, könnte es sein, das wir alle mit 4 Jahren eines Nachts von Ausschnitten aus unseren jetzigen Leben träumen?

Mal angenommen, wir träumen in dem ersten 4 Lebensjahren von z.B. 1.000.000 verschiedenen Leben, das wir in dem 4. Lebensjahr eines Nachts die letzten solcher Träume haben und kurz vorm Aufwachen wir von diesen Leben träumen, falls es alles unsere vergangene Leben sind und alles schon mal erlebt haben und wir all diese Leben auch immer und immer wieder bekommen.

Beispiele:

• 4jähriger A: träumt von dem Zeitraum 2015 - 2024 und erlebt in Laufe des Lebens einige Situationen in dem Zeitraum 2015 -2024 tatsächlich.
• 4jähriger B: träumt von dem Zeitraum 1990 - 1995 und erlebt in Laufe des Lebens einige Situationen in dem Zeitraum 1990 -1995 tatsächlich.
• 4jähriger C: träumt von dem Zeitraum 2002 - 2005 und erlebt in Laufe des Lebens einige Situationen in dem Zeitraum 2002 -2005 tatsächlich.

usw.

Was meint Ihr? Könnten Träume die Ursache für Deja vu Erlebnisse sein?

Hallo,

ich wollte fragen, welche die wohldefinierten Produkte sind und wie man darauf kommt? Danke im Vorraus!

Ich muss für eine Aufgabe erklären was eine Dioden Matrix ist

Hat jemand vielleicht eine einfache Erklärung?

Aufgabe:

Robinson Crusoe ist auf einer Insel gestranded, auf welcher die folgenden Wetterregeln gelten:

1. Der Übergang von schönem Wetter auf schlechtes Wetter sei genauso wahrscheinlich wie der Übergang von schlechtem auf schönes Wetter.

2. Ist es heute schön, so ist es in zwei Tagen mit einer Wahrscheinlichkeit von 68% wieder schön.

Wie groß sind die Übergangswahrscheinlichkeiten auf dieser Insel?

Problem/Ansatz:

Habe folgende Matrix :

soll die Determinante in Abhängigkeit von x bestimmen, nur sehe ich hier keinen Weg mehr nullen in eine Zeile oder Spalte zu bekommen. (übersehe ich was ) ? um dann den Entwicklungssatz durchzuführen ?

hat jemand eine Idee :) Danke

Hallo zusammen.. die Frage steht ja eigentlich schon oben.

Habt ihr noch Vor- und Nachteile parat?

Kann man z. B. bei der Matrix LED auch ohne den Matrix-Einsatz fahren? Also kann man das manuell einstellen?

Kann das Fernlicht manuell gesteuert werden?

danke und viele Grüße

Die Matrix ( 2 1) ist nicht diagonalisierbar, da die algebraische Vielfachheit vom

( 0 2)

Eigenwert 2 nämlich 2 ist, die geometrische jedoch 1.

Also algebraische ist größer als geometrische. Aber Ich kann doch theoretisch die 2. Zeile mal -0,5 nehmen und auf die erste draufrechnen, dann steht (2 0) in der Matrix. . (0 2)

Hier ist die Matrix ja dann wiederrum diagonal, sprich Ich hab Sie dann doch diagonalisiert. Irgendwas hab Ich falsch verstanden.

Danke im vorraus

Ich habe die Übergangsmatrix "P" gegeben, welche das Kaufverhalten aufzeigt und mit welcher Wahrscheinlichkeit die Kunden zu einem anderen Laden wechseln. Nun lautet die Aufgabe: Bestimmen Sie eine Gleichgewichtsverteilung für die Kundenzahlen, wenn die Supermärkte insgesamt 16000 Kunden haben.

Was wäre hierfür der Ansatz?

Wo würdet ihr die folgenden Punkte einordnen:

1. straßenbauunternehmen 
2. Wasserversorger in einer Gemeinde
3. Autos 
4. Benzin
5. Möbel 
6. Lokomotiven für deutsche Bahn

Nr 1 würde ich bei zweiseitiges polypol einordnen

Nr 2 : Angebotsmonopol 

Nr 3/4: Angebotsoligopol

Nr. 5: zweiseitiges polypol

Nr. 6: Nachfragenmonopol mit oligopolistischem Angebot 

Stimmt das so? 

Hallo,

ein arbeitskollege von mein vater meinte ich hätte matrix scheinwerfer im Passat.

Denn mein Vw passat hat DLA und sobald ich das fernlichtnach vorne drücke steht ein kleines A im fernlichtsymbol.

Was ich schon erfahren habe ich habe die High Vollled scheinwerfer.

Vw Passat 2x rline ez 11/2017 ist modell 18 190 PS DSG TDI

Letzte Frage.

Ich habe es mit Laplace versucht, aber ich habe am ende immer noch das a drinnen. Wie löse ich das? Wie berechne ich in diesem Fall die Determinante?

Hallo miteinander!

Wir haben gerade in Mathe Lk das Thema Matrizen bzw stochastische Prozesse.

Wir haben schon etliche Aufgaben darüber gemacht. Mein Problem an dieser ist, dass hier keine Wahrscheinlichkeiten oder so angegeben sind wie soll ich denn dann die Matrix aufstellen? Oder das Prozessdiagramm? Ich bekomme ja noch nicht Mal Nummer 1 hin.

Ich habe wahrscheinlich gerade einfach nur einen Denkfehler und stehe auf dem Schlauch, wäre lieb wenn mir jemand helfen könnte.

Lg

Wir haben dieses Thema erst seit gestern.

Was ich weiß ist, dass man von 2 Punkten die Vektoren berechnen kann, aber hier sind ja Punkte gesucht.. wie findet man die?

Bitte keine vollständigen Lösungen angeben, außer vielleicht bei einem Punkt als Beispiel. Ich will das können.

Danke für jede Hilfe.

kann man diese Matrix durch Apps lösen ? und bekommt die Ergebnisse

Ich habe mich mit existenziellen Fragen beschäftigt. Ob wir in einer Simulation leben und was passiert wenn diese Welt Fehler aufweist.

Und um herauszufinden wer uns simuliert hätte.

Es heißt ja, dass Tensoren die "Verallgemeinerung von Vektoren" sind.

Wir hatten auch, dass sich ein Tensor 2. Stufe als Matrix darstellen lässt und z. B. das Levi - Civita - Epsilon als Tensor 3. Stufe, was sich ja aber im Endeffekt auch als Hypermatrix verstehen lässt.

Was mir jetzt nicht so richtig klar geworden ist, ist:

1. In Welchem Sinne hat jetzt ein Tensor "mehrere Richtungen"? Kann man sich das z. B. für einen Tensor 2. Stufe wie einen Eigenvektor der dazugehörigen Matrix verstehen?
2. Kann man Tensoren nur als Vektor/Matrix/Hypermatrix darstellen, oder sind Vektoren/Matrizen/Hypermatrizen tatsächlich Tensoren 1./2./n. Stufe?

Wäre jeden dankbar der/die sich sich die Mühe macht es zu rechnen.

Ich habe mich gefragt ob es im dem Film die Matrix einen Gott gibt und wie dieser dargestellt ist. Ist es vielleicht Morpheus, oder doch Neo?

Kann mit jemand erklären wieso die 2. Lösung hier die richtige ist?

Hallo,

Wie genau wendet man die Matrix auf k an? (händisch)

Was passiert, wenn ich bei einer Matrix den Kern berechne und alle variablen sich als 0 ergeben? ist dann die Lösung also der Kern die leere menge? oder ist dann der Kern(A)=0 ?
Und was ist dann der rang des kerns?

Kann mir jemand den genaueren Unterschied erläutern? Beide werden ja benutzt, um Verformungen, Krümmungen oder Rotationen von Objekten zu beschreiben (z. B Relativitätstheorie-> raumzeitkrümmung tensoren). Gibt es da wesentliche unterschiede oder sind tensoren einfach Matrizen höherer Stufe?

Hey Leute,

ob eine 3x3 Matrix invertierbar ist oder nicht, finde ich ja herraus durch Betrachtung ob es quadratisch ist und ob die Determinante ungleich Null ist.

Wie kann ich eine NICHT invertierbare 3x3 Matrix OHNE herumzuprobieren finden?

Ich meine, ich könnte beliebig Zahlen finden und anschließend mit der Sarrus Regel die Determinate ermitteln, aber es gibt doch sicherlich einen effizientern Arbeitsweg ;)

Schon mal vielen Dank im Voraus

Ich stecke bei einer Aufgabe leider etwas fest.

Schreiben Sie ein Programm  Matrix, welches ein zweidimensionales Array übergeben bekommt und die Summe aller Werte in diesem Array berechnet.

Das erste, von der Konsole übergebene Argument, ist die Anzahl der Zeilen. Das zweite die Anzahl der Spalten des Arrays. Die restlichen Argumente sind Werte, mit denen das Array gefüllt werden soll. Gehen Sie davon aus, dass nur ganze Zahlen (positiv und negativ) übergeben werden.

Ihr Programm soll erst die Summe und anschließend die gesamte Matrix zeilenweise ausgeben. Falls zu wenige, oder zu viele Argumente von der Konsole übergeben werden oder die übergebenen Größenwerte negativ sind, soll Ihr Programm eine Fehlermeldung ausgeben, welche das Wort  ERROR enthält.

Eine Matrix der Größe 0 x 0

0×0 zählt als valide Matrix und hat die Summe $0$.

Ich habe bereits einen Ansatz zum Einlesen der Matrix. Dieser funktioniert aber nicht so ganz und ist noch unvollständig, da ich bei einigen Sachen nicht weiter komme.

Zum Beispiel, wie ich die Werte einlesen soll, nachdem ich die Spalte und Zeile eingelesen habe.

public class Matrix {
  public static void main(String[] args) {
    int zeile = Integer.parseInt(args[0]);
    int spalte = Integer.parseInt(args[1]);
    int Werte = Integer.parseInt(args[2]);
    int sum = 0;

    int[][] matrix = new int[zeile][spalte];

    for (int i = 0; i < zeile; i++) {
      for (int j = 0; j < spalte; j++) {
        matrix[i][j] = ???
        sum = matrix[i][j] + matrix[i][j];
      }

      System.out.println(sum);
      System.out.println(matrix[i][j]);
    }            

Hi Leute,

Was meint ihr? Ist die Welt, die wir glauben zu sehen wirklich echt oder nur fake?

Ist das was wir erleben vllt gar nicht echt, sondern nur vorprogrammiert? You know?

Wie steht ihr zu der Matrix-Theorie von Elon Musk und Nick Bostrom? ;-)

Was spricht dafür und was spricht dagegen? Welche Vor-/ Nachteile hat es? ._.

Vielen Dank für informative, interessante, hilfreiche, tolle & ausführliche Antworten! <3

Beim Multiplizieren von Matrizen muss ja die Anzahl der Spalten der ersten Matrix die gleiche Anzahl haben wie die Reihe der zweiten. Nun ist es aber so dass ja Einheits- und Nullmatrizen im Lehrbuch wie der Wert 1 oder 0 betrachtet wird. Aber Einzelwerte bzw. Einzelvektoren kann man ja mit einer Matrix multiplizieren unabhängig von ihrer Dimension.

Wäre cool wenn mich da jemand aufklären könnte.

hi,

was ist eigentlich der Unterschied zwischen Cytoplasma und Matrix? Ist das Cytoplasma ein allgemeiner Begriff für den Innenraum von Zellorganellen und Matrix ist dann spezifisch für die Mitochondrien?
Schonmal danke im Vorraus!!🙏🏻

Wenn man bei folgender Matrix den Rang bestimmen muss, gilt ja Zeilenrang=Spaltenrang. Alle Zeilen sind ja linear unabhängig und alle Spalten sind linear unabhängig. Zeilen gibt es jeweis 4 und Spalten 2 woher weiss man dann welches davon der Rang ist?

Ich muss diese Matrix in ELementarmatrizen (Produkt) umwandeln. Ich komme auf:

1. Vertausche 1 und 2
2. 2 = 1 + 2
3. 1 = 2 + 1
4. 3 = 3 * (1/2)
5. 3 = 3 - 2
6. Vertausche 3 und 2

In Elementarmatrizen wäre das:

1. P12
2. T21(1)
3. T12(1)
4. D3(1/2)
5. T32(-1)
6. P32

Und deren Produkt (von 6 zu 1) wäre dann meine Matrix. Stimmt das, oder gibt es im Internet online-Rechner dafür?

Wir sollen a und c machen. A habe ich fertig und mit einer Matrix a, b und c ausgerechnet und dann in eine Funktion geschrieben. Ich glaube zwar, dass mein Ergebnis ( f(x)= -2X^3+5X^2+X ) falsch ist, aber das ist gar nicht das Problem. Ich verstehe absolut nicht, was ich bei C machen soll. Ne Matrix werde ich ja offenbar nicht brauchen, sonst würde da ja nicht in der Aufgabe stehen, dass ich einen GTR bräuchte. Und selbst wenn, wie soll ich den Hochpunkt mit der X-Koordinate 2 verarbeiten?

Die Pillen:

Schluckst Du die blaue Pille, kehrst Du zurück in die heile Traumwelt, die die Matrix für Dich konstruiert hat. Die rote Pille dagegen wird Dir die Augen öffnen für die Welt, wie sie tatsächlich ist. ... Mit der roten Pille wachen wir auf. Wir sehen die ungeschminkte Realität, das echte Leben hinter der Scheinwelt.

Aufgabenteil a) und b) sind mir völlig klar.

Aber wie wird c berechnet, finde dazu nichts ähnliches in den Unterlagen. Besonders unklar ist mir der zweite Teil mit der Diagonalmatrix.

Ich habe die letzten Tage den Film Matrix gesehen und in der einen Szene, wo Morpheus erklärt, dass die Menschen nur noch Batterien für die Roboter sind, habe ich mich gefragt, wie das funktioniert. Laut dem Energieerhaltungsgesetz wird keine neue Energie erzeugt und auch keine verloren. Der Mensch selbst braucht aber Energie, um zu leben. Wie soll dieses Prinzip der menschlichen Batterie denn bitte funktionieren?

Hallo!

Wenn nach Eigenvektoren v zu einem Eigenwert w einer Matrix A gefragt wird suche ich zunächst immer nach kern(A-wE), also dem Eigenraum. (E ist nxn Einheitsmatrix). Danach suche ich mir einen der Basisvektoren des Eigenraums raus und habe einen Eigenvektor.

Jetzt habe ich im Internet verschiedene Notationen gesehen... Beim aufschreiben des Eigenraums: Beispiel: Eig(w)={t*v | t aus C}. t=0 wurde NICHT ausgeschlossen. Jemand anderes wiederum hat nach einem Eigenvektor gesucht und kam durch das lösen des LGS auf t*v und hat gesagt, dass t nicht Null sein darf... Deswegen bin ich ein bisschen verwirrt... ist die Null im Eigenraum, darf aber nicht als Eigenvektor gewählt werden?

Ich stieß eben auch auf eine Aufgabe, bei welcher ich sagen sollte ob es richtig oder falsch ist, dass (0,0,0)^T aus Q^3 Eigenvektor einer gegebenen Matrix ist...

Danke und LG

Hallo,

wie würde man den Drehwinkel errechnen, wenn man die Drehmatrix und die Drehachse gegeben hat?

Hallo.

Könnte mir jemand kurz erklären, wie man erkennt, ob eine Matrix diagonalisierbar ist und wie man sie, sofern sie diagonalisierbar ist, diagonalisiert?

Kann man etwas unendliches als "Unendlichkeit" definieren? Sobald man es definiert ist es etwas greifbares und nicht mehr unendlich. Kann man also sagen dass die Unendlichkeit ein Zustand ist oder nicht? Gibt es überhaupt eine Antwort darauf?

https://m.youtube.com/watch?v=m-nPQQWIf3c

Hallo. Das Orakel in Matrix soll ein Zeitvorherseher sein. Sie kennt die Zukunft... Ich hab mal reingeschaut. Sie sitzt da tatsächlich aus einem Grund, nämlich um von Smith absorbiert zu werden und wie wir später sehen, wird dieser neue Smith gegen Neo antreten und siegen, was Smith mit der "Source" (lol) verbindet und einen Neustart der Matrix auslöst...

Oder so in der Art hab ich es auf Englisch gelesen unter einem Video, das hieß Smith is the One (Not Neo). Also hatte Smith Recht, das Orakel saß da aus einem Grund. Aber warum zum Teufel hat sie die Kekse gebacken, die Smith 'zerstört' hat. Ahh wisst ihr was ich glaube ich kenn die Antwort. Sie mag es einfach Kekse zu backen. Aber wusste sie nicht, dass Smith sie zerstören wird? Ich weiß es ist nur ein Film, aber in Matrix hat alles versteckte Bedeutung.

Stehen die Kekse für freien Willen, die sie gebacken hat einfach so zum Spaß? Aber wie kann es freien Willen geben, wenn Smith und der ganze Film die Devise lauten wollen, dass Determinismus oder halt Kausalität alles beherrscht?

Hallo,

nehmen wir an ich habe so eine Matrix in Zeilenstufenform

Kann ich dim(Kern A) direkt ablesen, oder wie rechnet man das aus?

Danke im Vorraus, tue mich schwer mit dem Thema

Hallo,

Zu (2) fehlt mir irgendwie ein Ansatz. Ich muss doch nicht etwa die ganze Rechnung nur mit Variablen durchführen, oder doch? Gibt es eine Art "Diagonalisierbarkeits-Kriterium", d.h. bestimmte Eigenschaften, die mir die Diagonalisierbarkeit schenken, ohne, dass ich die diagonalisierte Matrix explizit angeben muss?

Hallo,

Was wäre dann hier die ZSF? Ich weiß, dass alles unterhalb der Hauptdiagonale 0 sein muss, das kriege ich auch hin. Nur bin ich mir bei nicht-quadratischen Matrizen nicht immer sicher.

Die Hauptdiagonalelemente sind ja 1, 1, 2

muss dann das Trapez unten (bestehend aus dem Block 0,-1,2,3 und 0).

Hallo,

hier die Definition...

Ich habe mal versucht, das nachzuvollziehen. Denn es soll dann später gelten, dass:

wobei v_B der Koordinantenvektor bezüglich der Basis B sein soll.

Mein Beispiel:

Ich wähle als Basis des V=IR² einmal die Standardbasis B=((1,0),(0,1)) und einmal W=IR² mit C=((1,2),(-1,1)).

Meine Lineare Abbildung F ist {{1,-1},{2,0}}·v (Matrix-Schreibweise wie in WolframAlpha). Ich verstehe das nun so:

F((1,0))=(1,2)

F((0,1))=(-1,0)

Nun frage ich mich, wie ich das in W mit den Basisvektoren aus C linearkombinieren kann:

(1,2)=ß_(1,1)·(1,2)+ß_(2,1)·(-1,1) => ß_(1,1)=1 und ß_(2,1)=0

(-1,0)=ß_(1,2)·(1,2)+ß_(2,2)·(-1,1) => ß_(1,2)-1/3 und ß_(2,2)=2/3

Dies fassen wir in eine 2x2-matrix zusammen: {{1,0},{-1/3,2/3}}.

Was soll nun bedeuten?

Ich verstehe das so, dass ich auf irgendeinen VEktor aus V die lineare Abbildung anwenden kann und das dann gleich der beschreibenden Matrix mal dem Koordinantenvektor ist.

v=3·(1,0)+2·(0,1)

F(3·(1,0)+2·(0,1))=3·F(1,0)+2·F(0,1)=3·(1,2)+2·(-1,0)=(1,6)

{{1,0},{-1/3,2/3}}·(3,2)=(3,1/3) und nicht (1,6). Was mache ich falsch?

Woran erkennt man hier an den Koeffizienten, dass Lambda 2 Null ist?

Hallo,

ich recherchiere gerade über Dreiecksmatrizen und habe auf Wikipedia folgende Aussage gefunden:

Kann man dass für alle n irgendwie induktiv zeigen? Mich würde ein Beweis interessieren ,der sich der Induktion bedient.

Wenn ich zum Beispiel herausfinden will, ob die vektoren eine Linearkombination bilden, dann muss ich ja eine Matrix bilden. Jedoch verstehe ich nicht, wie man diese deuten soll. Also angenommen da steht in der letzten zeile 0,0,1 oder 000 , was bedeutet das? Oder muss man gar nicht auf die letzte zeile gucken, sondern nur auf die Lösungen?

Danke im Voraus

Hallo,

undzwar wollte ich fragen wofür inverse Matrizen gebraucht werden?
Im Alltag oder in bestimmten Fachgebieten oder so...?

lieben Gruß !

Guten Abend,

ich habe in der Schule rechnen mit Matrizen gelernt und jetzt in meinen Studium wird das gerade erneut durchgenommen. Allerdings ist mir nicht ganz klar, wofür man das braucht. Könnte mir das bitte jemand erklären?

Ich bräuchte die einzelnen Umformungschritte

Hallo Leute,

ich lerne für einen Aufnahmetest. Die richtige Antwort ist das zweite Kästchen. Kann mir jemand erklären, warum? bin leicht verzweifelt.

Danke :-)

Ich Frage mich gerade folgendes:

Geben sei ein lineares Gleichungssystem:

(I) 3x + 2y + z = 4

(II) 3x + 2y + 0z = 5

(III) 3x + 2y + z = 4

Es stimmen (I) und (III) überein, darum gilt 0=0, dass GLS ist unterbestimmt und hat unendlich viele Lösungen.

Wenn ich das ganze jetzt geometrisch mit einer Matrixtransformation darstelle ergibt sich:

3 2 1

3 2 0 * (x|y|z) = (4|5|4)

3 2 1

Also suche ich den Vektor, der nach der Raumtransformation der Matrix gleich (4|5|4) ergibt.

Dafür brauche ich die Inverse Transformation der Matrix --> M^-1.

Da jedoch die Determinante DET(M) = 0 ergibt, da der Raum von 3d auf einen 2 oder 1 D Raum verzerrt wurde kann man diese Matrix nicht ermitteln.

Das lässt aus geometrischer Sicht ja jetzt die Frage offen, ob das GLS garkeine Lösung hat oder halt unendlich viele oder? Und wenn ja, lässt sich irgendwie bestimmen was von beiden der Fall ist?

Hallo zusammen,

ich habe eine klassische Turniertabelle, da je Excel leider nur Eingabe oder Ausgabefeld sein kann und niemals(zumindest nicht variierend) beides lässt sich nur eine Seite berechnen, während die andere eingetragen werden muss, somit habe für mein "Problem" beschlossen den gelben Bereich händisch einzutragen...

....und den anderen Bereich berechnen zu lassen. Nun gibt es bei dieser Tabelle nur 3 Möglichkeiten entweder Sieg (1), Niederlerage (0) oder Unentschieden (0,5), klar könnte ich das über eine simple WENN Abfrage erledigen, allerdings muss ich dabei fest auf eine Zelle festlegen, ich würde aber gerne eine Formel entwickeln mit der dynamisch unabhängig von der Spieleranzahl, also auch bei 6 oder 8 oder 10 Spielern das ganze eintragen kann ohne die Formel für jede Zelle erneut anzupassen.

Ich dachte somit an eine Forme die die Anhand eine Bezugszelle (in meinem Falle die erste oben links) die Position im Bereich kennt und nun ist es ja bei einer Kreuztabelle so dass die beiden von einander abhängigen Ergebnisse immer an der gleichen Stelle liegen nur Spalte und Zeile sind vertauscht.

Sprich wenn Spieler 2 gegen Spieler 3 spielt und gewinnt und dann trage ich in der 2 Zeile und in der 3 Spalte eine 1 ein und an der 3 Zeile und der 2 Spalte eine 0 - versteht ihr was ich meine?

Nur bin ich leider daran gescheitert, ich habe schon ein wenig versucht mit Indirekt und Index oder Vergleich herumzufummeln, ggf. Bereich verschieben, aber bin bisher kläglich gescheitert, da ich ja kein Ergebnis haben sondern eine aktuelle Position und die daraus resultierende Gegenposition.

Wenn ich das anschaulich nochmal darstellen soll, dann kann ich das gerne nochmal nachreichen, aber ich habe gehofft, dass man mir mit den Infos schon ein wenig weiterhelfen kann.

Kann mir da einer einen Tipp geben, wo ich ansetzen könnte, ich brauche keine vorgekaute Lösung, wenn jemand einen guten Ansatz hat, den er mir schmackhaft machen kann wäre mir schon sehr geholfen.

Vielen Dank schonmal an alle helfenden

Hallo,

Ich denke, dass es die Kardinalität dieser Teilmenge 3 ist, denn:

Nach welcher Logik wählt WolframAlpha die Basisvektoren aus?

Hi, Leute. Ich liebe die John-Wick-Filme und eigentlich generell Streifen mit Keanu Reeves. Wie findet ihr ihn? Mögt ihr seine Filme und wenn ja warum?

Danke im Voraus für eure Antworten :)

Hi Leute, meine Frage bezieht sich auf den Übergang wo ich ein Fragezeichen gezeichnet habe. Links davon steht ja was gemacht wurde von der originalen matrix zur zweiten. Aber dann steht da nichts mehr..

Vllt habt ihr ja einen Tipp.

Und hier steht ja oder; -a+b-2c..

Gibt es da zwei Formeln um das zu berechnen? Ich dachte alles wird mit dem erzeugendensystem berechnet.

Vielen Dank

Ich komme nicht mehr klar, kann mir jemand helfen, der weiter ist als ich?

er sollte eine psychedelische Substanz genommen haben(z.b.L...) und die Matrix Filme gesehen haben.

Das habe ich und ich habe viele Antworten bekommen, die aber wieder neue Fragen aufstellten!

Was soll ich tun? Ich weiß schon stellst nicht mehr, ob ich nun an einen Gott glauben soll, oder ob wir uns alle selbst geschaffen haben.

ich weiß nicht mehr,... ob Zeit existiert oder nicht, ob wir in der Matrix für immer feststecken?, weil die Menschheit es geschafft hat ewig zu leben, durch Maschinen, und die Simulation nun das ewige Leben darstellt, oder ob wir wirklich Batterien für die AI sind, die die Menscheit versklavt hat, also ob der Film nun eine Methaper ist, oder wirklichkeit. Ich bin mir 99,99999 prozent sicher dass wir in der Matrix leben, ich habe sie selbst gesehen.

Ich weiß nicht, welche Einstellung ich haben soll. Wenn der Mensch es weiter so macht wie bisher... dass wir versuchen uns weiter zu entwickeln, solange bis wir die schlauste künstliche Intelligenz erschaffen haben, dann wird die Matrix Realität, ob wir wollen oder nicht.

Ich weiß nicht ob wir es verhindern müssen oder nicht.

So viele Fragen, weiß jemand weiter?
Geht es jemandem genauso?

Glaubt ihr an die Matrix oder ist das für euch nur ein Schauermärchen der Science-Fiction-Literatur??

Ich möchte es wissen!

Ich bitte wie immer um ehrliche & schöne, ausführliche & interessante Antworten! <3

Ist alles nur ein Gedankenspiel. Also:

Angenommen, wir leben in einer Matrix (also alles was wir kennen, was wir sind usw. ist nur eine Simulation), gäbe es dann irgendeine Möglichkeit, wie man durch Zufall eben genau das herausfinden/beweisen könnte? Also dass wir in der Matrix leben?

PS: Grundvoraussetzung für diesen Gedanken ist natürlich, dass wir in einer Simulation leben.

Auf YouTube gibt es etliche Videos über Mandelbrot. Konnte jedoch leider nichts zu den Videos herausfinden... Wozu dient dieser schier endlose Zoom in etwas und warum brauchen Computer dafür mehrere Monate?

Hallo,

sei f(x)=x^TAx , A∈ℝ^(nxn). Ich möchte nun D_j f(x) bestimmen. Ich habe mir gedacht, dass man auf f(x)=(x^T)(Ax) die Produktregel anwenden kann. Das ist auch in der Musterlösung so, die da lautet:

Ich habe verstanden, warum die j-te Ableitung von x dann e_j ist. Aber das ganze Hin und Her mit dem Transponierten, was auch lustig von a_j^T auf x^T überspringt, komme ich nicht klar. Außerdem verstehe ich nicht, dass Ae_j=a_j^T ist - könnte da jemand vielleicht etwas Licht ins Dunkle bringen?

Frage steht oben, ich komme nicht weiter

Lg

Hallo! Ich habe nun schon ein paar Fragen zu Gerschgorin-Kreisen gestellt, jedoch hab ich immernoch offene Stellen bei denen ich Aufklärung benötige...

Ich habe also nun die Zeilen- und Spaltenkreise berechnet. Was genau nun? Ich wurde sagen: Vereinigung der Spaltenkreise bilden und die Vereinigung der Zeilenkreise bilden. Nun diese Beiden Vereinigungen schneiden und ich habe eine Menge in welcher die Eigenwerte liegen.

Möchte ich nun genauere Aussagen treffen bilde ich jeweils den Schnitt des ersten Spaltenkreises mit dem ersten Zeilenkreises. Dann den Schnitt des zweiten Spaltenkreises mit dem zweiten Zeilenkreis. ... Dann den Schnitt des n-ten Zeilenkreises mit dem n-ten Spaltenkreis. Jetzt habe ich diese n-vielen Schnitte und schaue mir an welche mit welchen disjunkt oder eben nicht disjunkt sind. Sind nun m- viele dieser n- vielen Schnitte nicht disjunkt liegen in der Vereinigung dieser m-vielen Schnitte genau m-viele Eigenwerte. Richtig?!?!? Und wie ist es mit der Algebrischen vielfachheit? Angenommen es überlappen sich 3 Kreise und die Eigenwerte sind a, b und nochmal b und c. In der Vereinigung dieser 3 Kreise liegen also 3 Eigenwerte. Kann es sein, dass a, b und wieder b in der Vereinigung liegen oder nicht, da b=b?

Vielen Dank und LG MAx Stuthmann

Der Körper muss ja zuerst schlafen, damit man weiter machen kann, aber ich hab so schiss davor (Schlaflähmung).

Ich merke wie mein Körper zuckt und alles richtig schwer wird und dann, wenn ich ´´schwebe´´, mach ich die Augen auf, und versuche so schnell wie möglich aus ihr rauszukommen.

Ich hab immer Angst, dass irgendein Typ etc mich anschaut, oder jemand mich an den Beinen packt!(Ich weiß, dass es nur in meinem Kopf spielt, aber trotzdem ist das gruselig)

Hi, könnt ihr mir vielleicht sagen, wieso diese Matrix den Rang 2 haben soll. Ich dachte es gilt Zeilenrang= Spaltenrang, wieso ist der Rang nicht 3?

Und ich wollte euch auch noch fragen, ob ich nicht für die Basis von im(f) auch einfach die beiden Spaltenvektoren als Basis verwenden dürfte ((1,1,3)^T,(3,-1,-1)^T), weil in den Lösungen auch hier etwas umständlicher vorgegangen wurde.

VG:)

Hallo

Ist die folgende Matrix mit Gaus ohne Pivoting lösbar?

Pivoting bedeutet ja, dass man die Zeilen so tauscht, dass das größte Element der Spalte (jeweils unter den Diagonalelementen) mit den Diagonalelement der Spalte getauscht wird und somit das neue Pivotelement wird.

Hier mal an dem Bsp ausgeführt:

Nun könnte ich per Rückwärtseinsetzen lösen

Nun haben wir aber nur das Gauß Verfahren und nachdem ich etwas umforme folgt

Wie würde es nun ohne Pivoting weitergehen? Geht es überhaupt weiter?

Hallo. Wenn eine Matrix von rechts/links invertierbar ist , ist dann die Abbildung injektiv oder sujektiv? Ich weiß wenn die Matrix invertierbar ist gilt bijektivität. Danke

Hi Leute, und zwar muss ich einen Wert für den Parameter C angeben, sodass das LGS bzw die Matrix keine Lösung, genau eine Lösung und unendlich viele Lösungen hat. Ich habe es bereits in Zeilenstufenform gebracht aber habe keinen Schimmer wie ich das ausrechnen soll .. habe versucht es mit der pq Formel zu berechnen aber es kamen komische bzw. Falsche werte heraus. Wenn mir jmd helfen könnte wäre ich euch sehr dankbar.

Hallo wie kann man bei einer Inversen Matrix überprüfen ob sie richtig ist, da man sich dort sehr schnell verrechnen kann. Danke im Voraus

Also ich hab es mit dem Entwicklungssatz gemacht, was ist denn aber das hier?

Ich bin echt lost und weiß schon beim 2. Schritt nicht weiter...

Wie soll ich denn 2 + i mit 4 + i eliminieren?

Darf man so die Spalten vertauschen?

Hallo,

sagen wir mal ich habe eine 3x2-Matrix, nennen wir sie A.

Für den Kern muss ja Ax=0 gelten. Ist das dann ein Vektor x derat, dass x=(u,v,w)? Wie geht das in diesem Fall?

Hallo, alle. Ich hätte eine Frage bezüglich einer Matheaufgabe. Wäre bitte jemand so nett und würde mir helfen? Sie lautet so:

"Gegeben ist f, ein Endomorphismus von IR^4, das folgendermaßen definiert ist:

f ist eine Projektion auf eine Hyperebene, gefolgt von einer Homothetie. Frage: Was ist das homothetische Verhältnis?" In anderen Worten, um wie viel wird hier vergrößert/verkleinert?

(Falls dies hilft, man kann die vierte Gleichung oben im Bild mithilfe von einer Linearkombination der anderen drei bekommen.)

Könnte mir jemand bitte helfen? Ich weiß hier leider nicht weiter…

Vielen Dank im Voraus!

Hallo! Ich habe letztens eine Frage zum Satz vin Courant-Fischer über Eigenwerte gefragt:

Jetzt habe ich noch eine Frage dazu: undzwar zum Teil:

min_(X aus X_i) max_(x aus X ungleich 0) [...]

Das ganze macht für mich keinen Sinn irgendwie... wäre beides max dann könnte ich mir das vorstellen im sinne von ich nehme den Unterraum sodass der Ausdruck für ein x aus diesem Unterraum maximal wird. Aber mit dem min über X aus X_i verstehe ich das nicht... ich würde gerne genauer fragen aber es fällt mir schwer das zu formulieren. Ich kann das min einfach nicht in einen Zusammenhang bringen hier...

Danke!! LG Max Stuthmann

Ich bin die Rechnung mehrmals durchgegangen und finde den Fehler nicht. Ein paar Einträge stimmen sogar :)

Vom Ansatz her stimmts aber, oder?

Hey, hierbei handelt es sich um eine Programmieraufgabe, und zwar soll eine 33x33 Matrix deklariert werden. Das hab ich so gemacht :

int test[33][33];

nun soll ich einen code schreiben wie die diagonalen der Matrix mit einander addiert werden und das Ergebnis soll ausgegeben werden. Kann mir jemanden sagen wie sowas aussehen soll?

Hallo,

wie würde ich von der Matrix {{1,1},{1,-1}} die Operatornorm berechnen?

Ich frage mich wie ich in Python ein Graphen als Adjazenzmatrix darstellte. Es sollte nicht in Listenform ( Liste=[ [2, 3] [6,8]] ) sein, wobei der äußere Listenindex eine Nummer für einen Knoten darstellt dem eine adjazenz zu geordnet werden soll.

Hallo, ich habe zu der angehängten Aufgabe eine Frage:

Zur Lösung dieser Aufgabe habe ich die Determinante von A in Abhängigkeit von Alfa und Beta berechnet und als Lösungssatz

"A ist surjektiv für alle Alfa, Beta aus R für die gilt 3Alfa-2Beta ungleich 0"

geschrieben.

Frage:

1. Reicht bei dieser Aufgabe der Ansatz, dass die Matrix surjektiv ist, sofern die Matrix regulär ist ( det(A) ungleich 0 )

2. Ist der Lösungssatz wie oben beschrieben ausreichend, oder muss ich das anders formulieren?

Für mein Studium muss ich zwei 8x8 Matrizen in ein Diagramm umwandeln, leider habe ich keine Ahnung, wie sowas funktioniert.

Das wären die Werte, welche ich umwandeln muss.

So sollte das Diagramm aussehen, wenn es fertig ist.

Ich hoffe, Ihr könnt mir helfen. Bin verzweifelt.

Danke im Voraus für eure Antworten.

Frage steht oben. (im R^n,n)
Kann mir jemand das Verfahren erklären? Wie gehe ich vor? Ich weiß wie diese Matrizen aussehen aber wie steht Dimension und Matrix überhaupt in Verbindung?

Gruß

Hallo Leute,

Ich habe folgende Aufgabe gemacht undzwar diese:

Ich muss nun die Anzahl der folgenden Lösungen angeben.

Wie geht das?

Hier ist die Zeilenstufenform von 1)-4)

1) (3 2 2)

(0 0 0)

(0 0 0)

(0 0 0)

2) (2 1 0)

(0 0 0)

(0 0 0)

(0 0 0)

3) (1 1 1 1)

(0 1 0 0)

4) (3 2 3)

(0 1 4)

Danke im Voraus

Am 21. Mai 2021 ist es dann soweit. Beide Filme werden am selben Tag gleichzeitig in den Kinos veröffentlicht. Auf welchen Film freut ihr euch mehr? Für mich ist Matrix 4 aufregender.

Hallo,

Ich suche eine Methode um den Index des Maximalwertes einer NP-Matrix-Reihe zu finden.

Bei einer Liste wuede ich ja einfach:

max_value = max(my_list)
max_index = my_list.index(max_value)

verwenden, bei einem Array/Matrix ist das jedoch nicht moeglich.

Kennt jemand einen Weg mein Problem zu loesen ohne jede einzelne Reihe in eine Liste umzuwandeln?

snr = ist in meinem Fall eine [512,6] Matrix
snr_list = []


for i in range(0,6):
  max_snr = max(snr[:, i])
  max_snr_index = ???
    
    
  snr_list.append(np.mean(snr[int(max_snr_index)-10:int(max_snr_index)+10, i]))
    
    

Dankeschoen.

Hallo ich stehe gerade ziemlich auf dem Schlauch, und finde auch im Internet nichts was meiner Aufgabe ähnlich ist.

Und zwar soll ich überprüfen ob 6 Vektoren:

v1= 1, -1, 0, 0 / v2= 1, 0, -1, 0 / v3= 1, 0, 0, 1 / v4= 0, 1, -1, 0 / v5= 0 ,1, 0, -1 / v6= 0, 0, 1, -1

eine Basis des R^4 bilden.

Wären es 3 oder 2 Vektoren hätte ich kein Problem damit, aber wie geht man bei 6 Vektoren vor? Alle in eine Matrix packen und dann Gaußverfahren?

Danke schonmal!

Jo habe gerade teil 1 gesehen, was haltet ihr von Teil 2 und Teil 3? Lohnt es sich sie anzugucken ? Habe oft gehört sie seien nicht so gut, deswegen die Frage.

Heute habe ich zufällig in der Stadt einen 10er und 20er Euro-Schein gefunden - beide ineinander gewickelt.

Als ich dann hinterher nochmals draußen war, bin ich nur durch Zufall über eine kleine Wiese gelaufen und dort habe ich dann einen 10er und 20er Zloty Schein (polnische Währung) gefunden - beide ineinander gewickelt.

Ist das ein Indiz, dass wir uns in einer Matrix befinden? Oder ist das nur ein Zufall? Falls es ein Zufall ist, wie wahrscheinlich wäre es dann, erst einen 10er- und 20er Euro-Schein auf einem Fleck, und hinterher dann noch einen 10er- und 20er Zloty-Schein auf einem Fleck zu finden?

Also es ist schon eine Weile her seid ich den Film gesehen habe und eigentlich fand ich ihn sehr schlecht, anders als alle anderen (besonders die so berühmte Zeitlupen Schuss Szene) aber egal UND ich habe bisher NUR den 1. Teil gesehen

Ich weiß, dass alles in der Welt nur virtuell ist und die Guten Neo als den Auserwählten halten und ihn deshalb in die wirkliche reale Welt rausholen.

Aber am Anfang in Büro warum wollen die Neo verhaften ? Wussten die Roboter zu der Zeit schon, dass er was besonderes ist.

Am Ende wird Neo doch erschossen und kurz danach steht er einfach wieder auf. Wie kann das sein ?? Sind das seine Superhelden Fähigkeiten welcher er ab dann hat ?

Werden in den anderen Teilen meine Fragen beantwortet ?

Kann mich evtl. jemand auf Quellen verweisen, die erklären, wie man solche Aufgaben löst?



Hallo zusammen,
weiß jemand wie diese Aufgabe zu lösen ist?

Hallo liebe Community,

es geht um die folgende Aufgabe:

Kann mir jemand sagen, welche Determinanten Umformregeln ich hier sinnvoll anwenden kann?

Eigentlich dachte ich, die Umformregeln bei Determinanten ganz gut drauf zu haben, aber hier macht doch weder das Ausklammern noch das Addieren/ Subtrahieren einzelner Zeilen bzw. Spalten Sinn.

In der Zeit hat man doch schon ganz schnell über den Laplace'schen Entwicklungssatz und dann die Sarrus'sche Regel die Determinanten berechnet...

Springt Euch eine Regel ins Auge, deren Anwendbarkeit Sinn macht?

Besten Dank im voraus!

Grüße carbonpilot01

Sorry wenn ich so oft nachfrage, ich verstehe es aber einfach nicht. Diese Aufgabe soll wohl sehr einfach sein, ich verstehe aber trotzdem nicht wie sie geht :(((

Ich hätte mir folgendes gedacht: Um die Abbildungsmatrix zu bestimmen, schau ich mir einfach die Bilder der Basisvektoren an. Leider verstehe ich nicht so ganz, was z denn jetzt sein soll. Einerseits wird z bei der Definition von IQ(3wurzel(5)) verwendet, andererseits ist das jetzt aber auch ein Element von IQ(3wurzel(5)). Das sind doch hoffentlich zwei unterschiedliche z, oder? Wenn z ein Element aus IQ(3wurzel(5)) ist, dann bedeutet das ja, dass z das hier ist:

 α,β,γ€IQ. Danach wird aber erst IQ(3wurzel(5)) als Vektorraum über IQ gesehen, dann wird die Abbildung Tz Endomorphismus vom IQ-Vektorraum IQ(3wurzel(5)) definiert, und wenn das z so wäre, wie ich es gesagt habe, dann wäre es ein Skalar, also kann das mit dem z ja schonmal nicht hinhauen, weil z ja kein Element aus IQ ist somit kein Skalar sein kann. Ich checke einfach nicht, wie dieses z denn nun aussehen soll. Das x ist ein Element aus dem Vektorraum, also ist x ein Vektor, der somit wiefolgt aussieht:

Wenn x jetzt ein Basisvektor ist, dann wären zwei Unbekannte 0, die übriggebliebene wäre 1. Und was nun? Ich verstehe einfach nicht, wie so ein z aussieht und was dann in der Abbildung mit den x und z passiert, kann mir das jemand erklären, danke :(

Kann mir hier bitte jemand helfen? Das wäre echt nett!☺

Ich schreibe nächstes Jahr mein Abitur und unser Lehrer lässt uns entscheiden ob wir das Thema Vekotorgeometrie oder Matrizen behandeln.
Ich habe mich schon umgehört und unsere Lehrer meinen Matrizen wäre um einiges kürzer vom stoff her und auch einfacher aber Freunde die beide Themen behandelt hatten meinten, dass Vektoren zwar mehr Stoff wäre aber leichter zu verstehen.

Was würdet ihr nehmen? Oder empfehlen?