Analysis – die neusten Beiträge

Hey liebe Community,

undzwar kann ich diese beiden Regel in der Differentialrechnung nicht voneinander unterscheiden, für mich sieht beides wie eine einfache Potenzregel aus.

Ich hoffe das mir jemand den Unterschied der beiden Regeln genau und möglichst einfach erklären kann.

Schon mal Danke im voraus!

Hallo liebe Community,

für das nachstehende Bild wollte ich die Wendepunkte berechnen. Da ich mir den Graph auch mal zeichnen lassen habe, ist für mich nur im Ursprung (0/0) ein Wendepunkt. Nachdem ich aber die 2. Ableitung = 0 gesetzt habe und x ausgeklammert habe, habe ich nicht nur 0 rausbekommen, sondern ~ +/- 3,46. Aber wo soll hier beim Graph ein Wendepunkt bei 3,46 und -3,46 sein?
Die Ableitung dürfte nicht falsch sein, denn ich habs nochmal mit einem Ableitungsrechner überprüft.

Wäre schön, wenn mir jemand auf die Sprünge helfen könnte :-) Danke!!

Und hier der Graph:

Hallo liebe Community,

ich verzweifle gerade an dieser Aufgabe:

Ich habe schon folgendes gelöst:

und hätte nun ein paar Fragen:
Könnte ihr generell mal schauen, ob das so passt?
Dann zu Aufgabe d) Vorzeichentabelle: So wie auf dem 4. Bild ganz oben haben wir immer eine Art Tabelle gemacht, z. B. die hier (ganz unten):

Aber kann ich hier überhaupt eine Tabelle machen? Ich habe ja ausgerechnet, dass ich keine Extremwerte habe, da der Graph so aussieht:

Dann wollte ich die Wendepunkte ausrechnen, obwohl das in der Aufgabenstellung nicht explizit stand. Wenn ich auf dem Graph schaue, liegt ja der Wendepunkt im Ursprung bei (0/0), denn da ändert sich ja das Richtungsverhalten der Kurve. Ich hatte eigentlich erwartet, dass ich 0 rausbekomme, aber da ich keine Lösung rausbekomme, heißt das doch so viel wie (wie auch bei den Extremstellen hier), dass ich keinen Wendepunkt habe.
Denke ich jetzt falsch oder habe ich mich verrechnet oder wie?
Wäre schön, wenn ihr mir das erklären könnt, ich sitz schon 2 Stunden hier und es ist schon nach halb 5 :-(

Dankeschön für alle Mühe und gut's Nächtle!

Wie berechne ich den Schnittpunkt dieser Funktionen? (Ich hab ein Bild angehängt)
Ich weiß, dass man gleichsetzen muss und dann nach x auflösen muss, aber wie das bei e Funktionen geht weiß ich nicht.

Danke im Voraus!:)

Hab zuerst Partiell integriert: arcsin(x)x - "integral"(x / Wurzel(1-x²))

Dann habe ich substituiert und bekam dann raus : - 1/2 * "integal" 1/ Wurzel(u) du

Als letzes habe ich aufgeleitet : -1/2 * [ x / Wurzel(u) ], dann halt rück-substituiert...laut meinem Lösungsheft ist mein Ergebnis falsch, kann mir einer die Aufgabe vorrechnen ? Danke

Tach,

ich bin letztens auf eine interessante Entdeckung gestoßen, nämlich folgendes:

Sind y = f(x) und y = g(x) zwei Funktionen, dann ist



die aus aus den Graphen von f und g entstehende Kurve.

Heißt so viel wie: Ich kann zwei Funktionsgraphen "aufeinanderkleben", indem ich die Funktionsgleichungen in die obige Gleichung einsetze. Veranschaulicht dargestellt:



Es ist eine Kurve, hier zusammengesetzt aus der Sinus- und der Kosinuskurve.

Warum aber funktioniert das - wie könnte man das erklären? Es ist leider etwas, an dessen Erklärung ich ein kleines bisschen verzweifle ;-)

Liebe Grüße.

Ich erlebe mich mal wieder total überfodert vom deutschen Bildungssystem und krieg nach mehrstündiger Recherche die einfachsten Grundlagen nicht auf die Kette.

Ich weiß, dass eine Abbildung linear ist, wenn gilt:

L1: f ( v + w) = f(v) + f(w)
L2: f ( λ * v) = λ * f(v)

So, jetzt bild ich aber vom R³ in den R² ab. Wie soll das denn bitte gehen?! Da bekommt doch jedes Element von R³ gar nicht alles aus R² zugewiesen. Soll ich jetzt x mit (x-z) addieren und y mit (z - y). Oder x mit 'x - z' und 'z-y' und danach y mit 'x-z' usw.? Oder soll man bei der b) den einen Vektor in den anderen reinpressen, weil sie miteinander verknüpft? Oder soll ich am besten gleich mein Traumstudium aufgeben und lieber zur Jura wechseln? Hilfe..:(

Weiß nämlich nicht was stetig heißt und Daniel Jung hats diesmal auch nicht gut erklärt.

Ich sitze schon seit 2 Stunden an der Aufgabe und brauche sie für morgen, kann mir eventuell jemand helfen?
Aufgabenstellung: Bestimmen Sie zu den abgebildeten Graphen jeweils eine mögliche Funktionsgleichung. Überlegen Sie zunächst, welchen Ansatz Sie für die Funktion wählen und welche Symmetrieeigenschaften Sie ausnutzen können.

Hallo,

bei einer Übungsaufgabe für die Uni geht es darum, ob gewisse Funktionen injektiv und surjektiv sind.

Dass f(x) = sin(x) nicht injektiv ist, ist mir klar. Das Problem ist, dass wir gegeben haben Q --> R. Und in den rationalen Zahlen gibt es ja kein Pi.

Oder kann ich mir einfach einen anderen beliebigen ganzzahligen x-Wert nehmen und für das resultierende f(x) einen weiteren x-Wert suchen? Bloß ich glaube dann komm ich wieder auf unendliche Zahlen und die sind glaube ich nicht in Q enthalten.

Also ich wäre dankbar für Hilfe

Hi, ich bin in der 11. Mathe LK

Und wollte mal fragen was ganzrationale Funktionen sind, wie ein Graph einer ganzr. Funktion aussieht und was keine ganzrationale Funktionen sind.

Danke.

n,m,k Element von den natürlichen Zahlen: n( m+k) = nm + nk.

Dabei darf nur das Assoziativgesetz und das Kommutativgesetz der Addition verwendet werden.

Ich habe überhaupt keine Ahnung, wie ich die Aufgabe 5b berechne... Ich brauche eure Hilfe! Könnte mir jemand rechnerisch zeigen, wie es geht?

Hallo Freunde, ich muss die gegebene Menge ( siehe Bild) als Vereinigung von Intervallen darstellen. Jedoch weiß ich absolut nicht wie das geht. Könnt ihr mir weiterhelfen

Man sagt ja immer, wenn bei f''(x) 0 rauskommt, lässt sich nix über f an dieser Stelle sagen, man greift also zum Vorzeichenwechselverfahren. Aber weiß jemand ein Beispiel, wo eben dieses f''(x) etwas anderes als einen Sattelpunkt bei f anzeigt?

Danke im Voraus (:

Ich frag mich wieso auf manchen Seiten im Internet bei der Fourier Transformation der Faktor 1/2sqrt(pi) vor der Formel steht und bei anderen nicht. Was ist der unterschied und wann sollte man es mit dem Faktor oder ohne berechnen?

Bei der Aufgabe Nr.4?

Untersuchen Sie die folgenden Mengen unter Verwendung von A = B ⇔ (A ⊂ B) ∧ (B ⊂ A) für zwei Mengen A und B auf Gleichheit:

(i) A = {z ∈ Z | es existiert ein m ∈ Z mit z = 7m + 4}, B = {z ∈ Z | es existiert ein m ∈ Z mit z = 7m − 3},

(ii) A = {z + z 0 ∈ Z | z, z0 ∈ Z}, B = {2z ∈ Z | z ∈ Z},

(iii) A = {(x, y) ∈ Q × Q | x + y = 3 und x − y = −5}, B = {(−1, 4)}.

Ich habe keine Ahnung wie ich bei solchen Aufgaben vorgehen muss. Könnt ihr mir für den Anfang helfen

Hallo zusammen,

stehe vor folgendem Problem:

Ich soll den/die Schnittpunkte der folgenden Funktionen miteinander berechnen.

f(x)= -3x^2+2x+4

g(x)= 2.wurzel(2x)

Ich habe die Funktionen wie gewohnt gleichgesetzt:

2.wurzel(2x) = -3x^2+2x+4

Dann habe ich beide Seiten quadriert:

(-3x^2+2x+4)(-3x^2+2x+4) = 2x

Ergibt:

9x^4-12x^3-20x^2+16x+16 = 2x

gekürzt:

9x^4-12x^3-20x^2+16x+16 = 2x

Dann ganz klassisch die 2x auf die andere Seite bringen:

9x^4-12x^3-20x^2+14x+16 = 0

Nun weiß ich nicht mehr weiter...

Polynomdivision? Aber ich kenne keine Nullstelle geschweige denn 2 Nullstellen...

Übersehe ich etwas ? gibt es einen Trick?

Freue mich auf eure Antworten!

Ist übrigens eine Aufgabe von meinem Bruder aus der 11. Klasse =)

Hab echt kein Plan wie ich die Aufgabe lösen kann.

Hallo zusammen,

ich möchte ein paar wenige Daten (Zahlen) von einer Excel Tabelle in eine andere kopieren, selbes Format. Eigentlich sollte es funktionieren. :)

Stattdessen taucht die Fehlermeldung "Mircosoft Excel kann die Datei nicht einfügen" auf. Was mache ich falsch?

Viele Grüße und Besten Dank!

Ich schreibe morgen Kurztest in Mathe über gebrochene rationale Funktionen und fürs faktorisieren mancher Terme habe ich bis jetzt nur Mitternachtsformel, Binomische formeln und allgemeines faktorisieren verwendet. Nun habe ich aber eine Funktion die lautet f(x)= 3x / x^3 - 3x +2 Und mir scheint's als könnte ich da eine Polynom Division durchführen. Leider finde ich meine alten Arbeitsblätter vom letzten Jahr dazu nicht und ich bin mir nicht ganz sicher ob dies nur für ein Polynom mit vier Termen gilt oder nicht. Und ob ich ein x^2 in meinen Polynom brauche. Welche sind überhaupt die allgemeinen Voraussetzungen für Polynom Division? Danke im Vorraus

Funktion: fa(x)=2ax^3+2x-4a*x

Nehmen wir an wir haben ein Funktion f(x)=x+1. das ist ja das gleiche wie f(x)=x^1+1x^0 wenn wir jetzt ableiten teilt man ja durch x bzw x^1 doch statt 1 wie es sein sollte kommt jetzt 1,1 raus! Wie kann das sein? (x^1+1x^0)/x^1

Hey wir sollen Nr. 4 machen, jedoch weiß ich nicht wie ich die Punkte ablesen soll. Also welche Maße die Achsen haben.  

Danke für Hilfe

Hallo Leute! Habe mega Schwierigkeiten bei der Lösung folgender Aufgabe:

Eine Kugel der Masse m trifft (zur Zeit t = 0) mit der Geschwindigkeit v0 senkrecht auf eine „kugelsichere Weste“ auf, ein viskoses Medium, d.h. die Abbremsung der Kugel soll ausschließlich durch Reibung erfolgen. Die Reibungskraft ist proportional zur Geschwindigkeit der Kugel: Fr = −k * v (k = Reibungskoeffizient).

a) Stelle Sie die Differentialgleichung für v(t) auf!

b) Wie lautet die allgemeine Lösung dieser DGL?

c) Wie lautet die spezielle Lösung?

d) Wie groß ist die Eindringtiefe s(t) der Kugel in Abhängigkeit der Zeit t?

e) Wie dick sollte die kugelsiere Weste mindestens sein?

Vielen Dank im voraus!

Dies ist keine Hausaufgabe, sondenr lediglich eine Vorbereitungsaufgabe auf eine Klausur. Ich habe noch nie so einen Typ von Aufgabe bearbeitet!

Folgene Aufgabe: Wie kommt man drauf?

f(t) (t in Jahren, f(t) in Millionen) beschreibt die Zahl der Einwohner in Deutschland seit 1995.

Interpretieren Sie f(5)=82,0 und f(6) - f (5,5) : 6 -5,5 = -0,1 

Geben Sie jeweils die Einheit an.

Antwort:

Im Jahr 2000 hat Deutschland 82 Millionen Einwohner. Zwischen 2000 und 2001, genauer gesagt in der zweiten Hälfte des Jahres 2000, ist die Bevölkerung durchschnittlich um 100.000 (0,1 Millionen) Einwohner gesunken

Doch wie kommt man darauf ?

Ich bedanke mich im Voraus!!!

hier ein Bild zur Verdeutlichung! Bitte sagt mir, ob ich es richtig gemacht habe!

Danke schonmal :).

Hallo Leute

Wir haben gerade ein neues Thema und ich versuche es gerade zwei Aufgaben zu lösen allerdings habe ich ein paar Probleme könntet ihr mir bitte helfen ich und mir das auch vielleicht erklären?

Ich soll nächste Woche diese Aufgabe vorrechnen und ich habe keine Ahnung, wie ich da ran gehe. Könnt ihr mir helfen?

Die Aufgabe lautet:

Eine Boje soll aus Stahlblech zu einer Hohlkugel geformt werden. Die Dichte beträgt 7,8 g/cm³ und der Innendurchmesser 40cm. Sie soll 30 cm in das Wasser eintauchen. Die Frage lautet: Welche Wandstärke muss gewählt werden?

Ich weiß wir müssen das Volumen berechnen, welches in das Wasser eintaucht. Und dann die Masse.

Ist das richtig? Wie muss ich weiter rechnen?

Hallo zsm,

Ich möchte versuchen diese Gleichung in eine Scheitelpunktsform bringen:

0,5x^2+x-2,5

Ich weiß dass man es mithilfe quadratischer Ergänzung lösen kann. Ich habe allerdings versucht es so zu lösen bzw. umformen. Das Problem ist, ich komme zum falschen Ergebnis wobei ich denke, dass ich doch richtig rechne, kann es mir aber nicht erklären. Ich werde 2 Rechenwege aufschreiben (ich weiß, im Prinzip ist es fast das gleiche, aber es macht schon einen Unterschied für mich ob ich es auf eigene Faust lösen möchte oder blind einem System folge).

Meine Versuchung:

1. 0,5x^2+x-2,5 | /0,5 (x^2 muss stehen, deshalb teilt man den Rest auch durch 0,5)

2. x^2+2x-5 | aus x^2+2x mache ich ein Binom.

3. (x+1)^2 -1-5 | Doch aus dem Binom verbleibt die 1, die ziehe ich von der Gegenseite (5) ab, ich meine was ich von x was wegnehme muss ich es auch bei 5 auch tun.

4. (x+1)^2-6

Scheitelpunk (-1|-6)

Nun jetzt aber alles nach Regeln der Quadratischer Ergänzung:

1. 0,5x^2+x-2,5 | /0,5
2. 0,5(x^2+2x-5) | quadratisch ergänzen
3. 0,5((x+1)^2+1-1-5) | klammer auflösen
4. 0,5(x+1)^2-3

Scheitelpunkt (-1|-3)

Wie ihr erkennt ist, ist mein S falsch. Die -6 müsste noch mit 0,5 multipliziert werden damit ich auf -3 komme. Ich verstehe aber nicht warum muss ich das tun, wenn ich am Anfang doch schon alles mit 0,5 dividiert habe, ich meine die 0,5 habe ich somit eliminiert, warum muss ich dann wieder mit 0,5 multiplizieren, es entsteht doch eine Ungleichheit??

Ich bitte um eine gute Erklärung, wäre dafür sehr sehr Dankbar.

Hallo!

Leider habe ich eine etwas knifflige Aufgabe vor mir. Es geht um das Stoßprozess zweier Teilchen und ich muss den Winkel des ersten Teilchens nach dem Stoß und die jeweiligen Geschwindigkeiten rausfinden.
Ich habe jetzt ein lineares Gleichungssystem erstellt mit den drei Variablen. Nur blöderweise kann ich das LGS nicht lösen!

Ich wäre euch sehr dankbar, wenn ihr mir helfen würdet.

Danke!

Ist der Unterschied erheblich?

Gegeben ist eine Zeit-Ort-Funktion [m] in Abhängigkeit von t [s].

Aufgabe: Näherungsweise die momentane Geschindigkeit bei t=3 berechnen!

s(t)=0,6t^2+2t

Bitte kann mir jemand den Rechenweg erklären, denn ich verstehe nicht, wie man den Limes "händisch" berechnet. Den Trick mit den binomischen Formeln habe ich schon ausprobiert:/.

Als Lösung sollte 5,6 m/s rauskommen.

Liebe Grüße und es wäre echt cool, wenn jemand die Frage heute noch beantworten könnte:)

LG <3

Hallo Leute :) ich habe angefangen für die Matheklausur zur lernen (Abitur) und zum erstenmal habe ich eine Aufgabe wo ich wirklich garnichts weiß was ich machen muss noch nicht mal den Ansatz. Kann mir jemand die Aufgabe erklären bzw sagen was mann in den einzelnen Teilaufgaben machen muss . Wäre Lieb danke. Aufgabe 1 auf dem Bild

Hallo, mache demnächst mündliches abitur und wollte mal fragen, wie man solche Aufgaben löst. Es geht hier um Schnittpunkte von Funktionen. Ich weiß den Ablauf und brauche keine Erklärungen, jedoch habe ich noch nie verstanden, wie man sowas wie im Bild nach X auflösen kann. Würde mich über Hilfe freuen (: Lg

Gegebene Funktion: fa(x) = a(x^3 + 2x^2 - 7x + 4) mit Dfa= R, a=R und a>0. Folgende Aufgabe: Berechnen Sie den Wert für a so, dass die Tangente an den Graphen der Funktion fa an der Stelle x=-3 die y-Achse bei y=5 schneidet.

Kann mir jemand erklären wie man das angeht? Danke!!! :)

Ich soll bei Aufgabe b eine ganze Reihe ableiten. Hat jemand eine Idee wie das funktioniert 🤔

Hallo, Community,

morgen ist bundesweit das Matheabitur und ich habe nach 2 Jahren immernoch wenig Ahnung von Analysis. Kann mir jemand, z.B. in der Kurvendiskussion Stichwörter geben, die einem zeigen, was man machen soll? "Wann kann ich z.B. f (x) nullsetzen, oder wann soll ich f(x) immer ableiten? Je mehr "Stichwörter", desto besser!
Mit lieben Grüßen

HowtoIQ

Hey , kann mir jemand sagen wie man die Folge auf Konvergenz untersucht? Die Sache, die ich nicht verstehe: ist die Folge überhaupt konvergent und wenn ja, was ist ihr Grenzwert?
Lg und Danke im Voraus

Was mache ich falsch? Danke an die Mathebrains..

Hey!

Ich frage mich, ob es denn eine Funktion gibt, welche monoton fallend und stetig ist, welche aber nicht differenzierbar ist.

Gibt es solch eine Funktion?

Hallo zusammen,

seit langem schon stört mich diese Frage: Es heißt immer bei Funktionen/Abbildungen etc., dass einem x-Wert genau ein y-Wert zugeordnet wird usw..

Warum aber geht dann der Pfeil von x nach y? Das macht doch keinen Sinn, schließlich wird der y-Wert doch dem x-Wert zugeordnet.

Hat das jemand von euch vielleicht besser verstanden als ich? :D

Kann mir jemand die Zwischenschritte zur Bildung der Ableitung dieser Funktion nennen? Hab es jetzt mit der Produktregel versucht und es stimmt nicht mit der Lösung überein, kann jemand helfen?

Vom Koordinaten Ursprung (0/0) Wird die Tangente an den Graphen der Funktion f mit f(x)=x^2 +2 gezeichnet.

Laut Lösung ist die Tangentengleichung y=2 X Wurzel2 X x.

Wie kommt man darauf?

Kann ich beim Betrachten einer Koordinatenform für eine Ebene, beispielsweise 5x+2y+4z=12, an der Zahl 12 bereits irgendeine Information gewinnen?

Kann mir jemand sagen wie ich die Funktion unterteilen soll? Ich habe ja keine konkrete obere Grenze, sondern nur ein x 🤔?

Ich schreibe morgen Klausur und es wird sehr wahrscheinlich diese Textaufgabe mit anderen Zahlen dran kommen.

Ich hab zwei Bilder angehangen und bei beiden verstehe ich das mit der Zeit nicht.

Bei Aufgabe 5: da steht das die Zeit von 10:00 bis 19:30 geht. Wenn ich dann bei a) das nach 3 Stunden berechnen soll, muss ich dann 13 einsetzen oder 3 und warum?

Bei Aufgabe 4 dasselbe ich weiß nicht ob ich den Zeitpunkt oder die Stunden eintragen soll

Könnt ihr mir vllt erklären wann da jetzt als Beispiel 3 hin müsste und wann 13?

Ich hoffe man kann mein Problem verstehe. 😅

Wie soll man das bitte beweisen? Wie kann man überhaupt einen Beweis aufstellen?

Hallo! Hab mir dazu paar Überlegungen aufgeschrieben. (Aufgabe 6)

Hallo Leute,

bedauerlicherweise, habe ich als ich diese Aufgabe durchgerechnet habe sehr spät realisiert, dass ich keine Lösungen habe...

http://ne.lo-net2.de/selbstlernmaterial/m/abi/BB/12_Ma_Aufgaben_LK.pdf die 4. Seite die Raubvogelaufgabe

meine lösungen:

zu a.) die geschwindigkeiten sind klar... für den Abstand habe ich 22,1 m raus

b.) habe auch das Kontrollergebnis, nur es hat mich verwirrt weil da stand das die Ebene e orthogonal zu dem Vektor ist, d.h ja eigentlich das diese ebene einen normalenvektor besitzen muss der im skalarprodukt mit dem gegebenen vektor 0 ergibt... naja jedenfalls habe ich das ergebnis r= 300 dh 300s und der winkel ca 1,26*

bei c.) habe ich den abstand 90 m raus, da habe ich für die geradengleichung des raubvogels auch r=300 eingesetzt, weil in der aufgabe stand ''in diesem moment'

bei dem winkel war ich mir nicht ganz sicher.. ich habe den rv des raubvogels und den rv des singvogels gewählt, dh den schnittwinkel der geraden... ca 20,83

bei d.) wusste ich nicht recht, wie ich es berechnen soll... als ansatz hatte ich die geschwindigkeiten für den raubvogel 183.6 km pro stunde weil der ja 3 mal so schnell fliegen kann und der singvogel 27 km pro stunde

Ich habe die Funktion x/x^2-k gegeben.
Die Ableitungen hab ich schon berechnet und zwar
1.te Ableitung : (-x^2-k)/(x^2-k)^2
2.te Ableitung : (2x^5+4kx^3-6k^2x)/(x^2-k)^4
Nur leider weiß ich nicht wie man mit einem Parameter erkennen kann, was der Hochpunkt und Tiefpunkt ist. Man muss ja den x-wert, den man in der ersten Ableitung herausbekommen hat, in die zweite Ableitung einsetzen, um herauszufinden , was Hoch und was Tiefpunkt ist, aber ich kann das irgendwie nicht. Kann mir da jemand helfen?

Hallo:)

wir machen im Moment Analysis also Bestimmung der Extrempunkte und das Vorgehen verstehe ich schon, aber ich frage mich, wozu man die hinreichende Bedingung nun benötigt?

Also bei der ersten Ableitung untersucht man doch, an welchen Stellen man eine Nullstelle, also eine waagerechte Tangente, hat (und an den Stellen muss dann ja bei f eine Extremstelle vorliegen).

Aber warum darf bei der zweiten Aböeitung diese Stelle nicht gleich 0 sein? Wahrscheinlich ist die Frage eh ur blöd, aber ich steh grad völlig auf dem Schlauch. Danke schonmal:)

Wenn das hinreichende Kriterium nicht erfüllt ist, also die kritischen Punkte in der Hessematrix z.B. die Nullmatrix ergibt, heißt das, dass wir keine lokalen Extrema haben oder, dass wir lediglich keine Aussagen über lokale Extrema treffen können?

Lg

Siehe Bilder

Hallo, ich schreibe morgen Mathe Abitur und bin mir nicht sicher, was die Definition des Operators "bestimmen" meint.

Kann ich das Integral einfach in den Taschenrechner eintippen oder muss ich noch eine Stammfunktion angeben als Zwischenschritt?

Die stärkste Abnahme einer Funktion würde ich mithilfe der zweiten (und dritten) Ableitung ausrechnen, da die stärkste Abnahme ein Wendepunkt ist und f''(x) = 0, f'''(x) =/= 0 gilt.

Nun muss ich die stärkste Abnahme der momentanen Änderungsrate ausrechnen. Heißt das, ich gehe wie oben vor, nut mit f'''(x)=0 und f''''(x) =/= 0 der originalen Funktion?

Ich weiß, wie man die Nullstellen dieser funktion berechnet sin(2x) = 0 --> 2x = k × Pi x = k/2 × Pi (k element von ganzen Zahlen) wenn die NST jetzt imIntervall von (0;Pi) sein müssten wäre die Nullstellen ja 1. für k=0 --> x=0 2. für k =1 --> x=0,5 Pi 3. für k=2 --> x = Pi

wie geht das ganze bei dieser funktion 2sin (2x+1) +1 =0

kann mit jmd helfen?

Ist es möglich, bei einer beliebigen, periodischen Funktion f(x) die Nullstellen in einem bestimmten Intervall [a;b] zu berechnen?

Z.B. bei der Funktion f(x) = 2+cos(x)/sin^2(x) im Intervall [0;π]

Ich wollte gerne wissen, wie man beispielsweise bei einer Polynomdivision die erste Nullstelle errät, wenn man immer diese Parameter dabei hat, deren echte Zahl man natürlich nicht kennt.

Wenn ich mir die Funktion (-log(x))^-1 im halb offenen Intervall anschaue (1,e] dann ist ja der Grenzwert fuer x->1 -unendlich. Ist das dann auch ein lokales Minimum?

Wenn man z.B. eine Funktion hat und zeigen soll, dass diese stetig ist, dann fängt man ja meistens so an, dass man sich das aufschreibt, was kleiner sein soll als Epsilon und dann formt man um und schätzt ab, bis da irgendwas steht , wie

Ix-x0I<... und dann setzt man diesen Term, welche größer ist als Ix-x0I als Delta. Je nach dem, ob dann der Term nur von Epsilon oder von Epsilon und x0 abhängt, ist die Funktion dann stetig oder gleichmäßig stetig. Geht das immer nach diesem Schema ?

1) Bestimmen sie alle tanzrationalen Funktionen vom Grad 3, deren Graphen symmetrisch zum Ursprung sind und die x-achse an der stelle x = 2 schneiden

2) Bestimmen Sie eine ganzrationale Funktion dritten Grades, deren Graph durch die Punkte A(2|6), B(0|4), C(3|5,5) und D(–2|8) geht. 

wie funktioniert das ?

Ich habe eine Frage zu folgender Aufgabe: Bestimmen Sie näherungsweise die Ableitung der Funktion f(x)=x^2 an der Stelle x0=2 mithilfe des Differenzenquotienten für kleine Werte von h.

Bitte dringend um Hilfe, vielen Dank im Voraus!

Hallo,
ich bräuchte Hilfe, wie ich davon die Ableitung bilde, ich hab es schon länger versucht, aber irgendwie bekomme ich nicht das richtige Ergebnis heraus. Bitte mit Rechenweg, denn die Lösung weiß ich schon, nur noch nicht, wie ich dahin komme.
Vielen Dank im voraus

Hallo Leute, ich brauche dringend Hilfe bei dieser Aufgabe:

https://www.iqb.hu-berlin.de/abitur/pools2017/abitur/pools2017/mathematik/erhoeht/2017_M_erhoeht_B_6.pdf

also bei e.) habe ich es verstanden, nur warum wird da durch cos geteilt?

bei f.) hatte ich überhaupt keine Ahnung, da würde ich ja eigentlich etwas mit dem Mittelpunkt anfangen können, also ich dachte das ich einfach die Strecke von A zu M als radius angebe mit dem Betrag..

g.) Es gab noch eine Zusatzaufgabe unzwar: Ermitteln Sie die Koordinaten des Eckpunkts A, nachdem das Metallrohr um 180 grad gedreht wurde. Ein möglicher Normalenvektor der ebene, in der sich die Modulfläche in der Ausgangsposition befindet ist (3/-1/5) Ermitteln Sie einen Normalenvektor für die Modulfläche nach einer Drehung von 180 Grad.

Aufleitung mit Integration

Hi,

ich muss eine Matheaufgabe lösen die so lautet:

Eine ganzrationale Funktion 4. Grades verläuft durch den Punkt P(-2/4) und besitzt im Ursprung des Koordinatensystem ein relatives Minimum. Die Steigung der Tangente an der Stelle Nullstelle x=-1 beträgt 3.

Jetzt brauche ich ja die Bedingungen um die Gleichung zu lösen. Eine davon ist ja einfach der gegebene Punkt aber ich verstehe das mit dem Minimum und der Steigung nicht. Kann mir jemand das erklären bzw in welche Formel (Ausgangsformel, Ableitung oder 2. Ableitung) muss ich das einsetzten? Und brauche ich 3 oder 4 bedingungen?

Danke im voraus

Hallo Leute,

in diesem Link http://lucaslucas.org/data/documents/Langzeit-Klausur-Mathematik-2017.pdf die 5. Seite Teilaufgabe b.) sieht ihr eine Tabelle, in der man die prozentualen Abweichungen bestimmen soll, bzw. ergänzen soll... ich komme nicht auf die in der Tabelle bereits ausgefüllten prozentualen Abweichungen.. Wie kommt man auf diese Prozentwerte?

Ich habe eine Funktion f(x,y), die R^2 nach R abbildet. Ist die Aussage, dass für ein bestimmtes (x_1,y_1) zwei Richtungsableitungen null sind, äquivalent zu der Aussage, dass der Gradient an der selben Stelle (x_1,y_1) null ist?

Hallo ihr Lieben,

in Mathe haben wir letzte Stunde das Globalverhalten besprochen.

Leider verstehe ich dies überhaupt nicht und bald steht auch schon die Matheklausur an...

Könnte mir eventuell jemand dies anhand der beiden unten stehenden Funktionen erklären?

f(x)=e hoch 3x

g(x)=xe hoch x

Liebe Grüße und danke im Voraus!

flowerpowerfee

Ein Fixpunktsatz

Es sei f: [0,1]-->R eine stetige Funktion, so dass für alle x ist element von [0,1]: 0 ist kleiner-gleich f(x) ist kleiner-gleich 1.

Beweisen Sie, dass es eine Zahl x0 ist element von [0,1] gibt, für die f(x0)=x0 gilt

Hallo Leute,

ich rechne gerade die IQB Aufgaben durch und bin bei einer total verzweifelt, sie lautet:

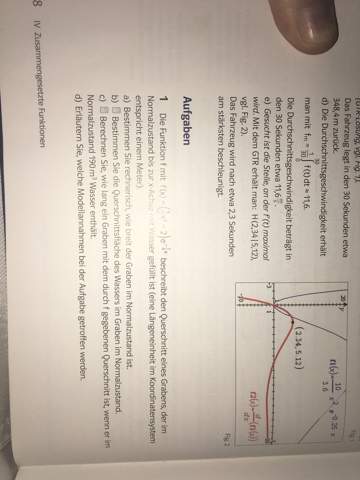
2 Für ein anderes Becken wird die momentane Änderungsrate des Volumens des enthaltenen Wassers für 0 ≤ t ≤ 15 durch die Funktion g mit g(t)= 0,8t^3- 15,6t^2 +72t beschrieben. Dabei ist t die seit Beobachtungsbeginn vergangene Zeit in Stunden und g(t) die Änderungsrate in Kubikmeter pro h . Die Funktion G(t)= 0.2t^4 - 5,2t^3+36t^2 ist eine Stammfunktion von g.

a Berechnen Sie für den beschriebenen Zeitraum denjenigen Zeitpunkt, zu dem die momentane Änderungsrate des Wasservolumens maximal ist.

b Ermitteln Sie rechnerisch den Zeitraum, in dem das Volumen des Wassers abnimmt.

c Drei Stunden nach Beobachtungsbeginn sind im Becken 350 Kubikmeter Wasser enthalten. Bestimmen Sie das Volumen des Wassers zu Beobachtungsbeginn.

d Untersuchen Sie rechnerisch, ob es nach Beobachtungsbeginn einen Zeitpunkt gibt, zu dem das Wasservolumen ebenso groß ist wie zu Beobachtungsbeginn. 

zu a.): ich bin so vorgegangen, dass ich die Extrempunkte ausgerechnet habe mithilfe der 1. Ableitung, bei t=3 ist ein HP, ich habe auch die funktion gezeichnet, aber in der Lösung steht, dass es der Zeitpunkt t=15 ist was ich absolut nicht nachvollziehen kann. Bei t=15 beträgt die mom. Änderungsrate 250, beim Hochpunkt nur 97,2..

b.) dort, habe ich direkt an das Monotonieverhalten gedacht, deshalb hab ich mithilfe der 1. Ableitung ermittelt, wann die Funktion steigend bzw fallend ist. In der Lösung haben die jedoch die grundfunktion also g(t)benutzt.. liegt es daran, dass die Funktion schon die Steigung also die mom. Änderung angibt?

c.)

bei c stand in der Lösung dass die 350 - das Integral mit den Grenzen 0 bis 3 verwendet haben.. liegt es daran weil, der Flächeninhalt eigentlich zwischen 0 und 3, 199,8 beträgt, aber es 350 betragen muss und die deswegen die 199,8 von der 350 abziehen?

d.) bei d haben die das uneigentliche Integral verwendet, bei dem die obere Grenze fehlt. Bis hier hin konnte ich es nachvollziehen, aber die haben es nicht mit der 150 gleichgesetzt sondern mit der 0.. obwohl man in Teilaufgabe c ermittelt hat, dass das Volumen zu Beginn 150 FE beträgt..

Man berechnet ja mit all diesen Methoden die Stammfunktion. Aber was sind die Anzeichen einer Funktion wann ich welche der oben genannten Methoden nehme ?

Ich habe folgende Funktion zu lösen:

f: (-3, -1] -> IR

f(x) = |2x+3|

Ich habe schon bewiesen, unter welcher Bedingung die Funktion diff'bar ist.

Nun stell man bei der Berechnung der ersten Ableitung, dass es ungleich null ist. Wie kann man dann weitermachen? btw. was lässt sich denn behaupten?

Ich bedanke mich bei euch im Voraus

Tschüß!

Hallo ihr Lieben,
Ich sitze gerade mal wieder über meinen Mare Sachen und versuche die Aufgabe 11 zu lösen. Ich habe bereits Punkte markiert, bei denen ich dachte, dass sie mir helfen könnten, die kubische Parabel zu rekonstruieren. Nur komme ich einfach nicht weiter und verzweifle. Es wäre ganz lieb, wenn mir jemand Helfen könnte. Danke schon einmal im Voraus.

Ich habe eben schon mal eine Frage dazu gestellt.. jetzt hat unser Lehrer eben per Mail eine Zusatzinformation geschickt, weil die Aufgabe sonnst nicht stimmt (typisch Schulbuch :D)

Die Aufgabe nochmal:

Paul trinkt seinen Tee am liebsten 80°C heis, die Raumtemperatur beträgt 20°C.Die Temperatur von dem Tee sinkt im Raum um 10% der Differenz zwischen aktueller Temperatur und Raum temperatur pro Minute.

Stelle einen Finktionsterm auf und berechne die Temperatur von dem Tee nach 10 Minuten.

Meine Überlegungen:

Formel Begrenztes Wachstum: f(x)= S+(f(0)-S)·e^(-k·x)

s= 20

f(0)= 80

x= 10 (Minuten)

Was wäre dann in diesem Fall k?

Danke nochmal :)

Hallo,

wie genau integriert man diese Funktion? dx/(√x +1 /(√x)). Macht man das mit Substitution und wenn ja wie?

Danke im Voraus;)

Ich hab eine Reihe, welche die folge An aufsummiert. diese Folge ist 1/n falls n ungerade und 1/n^2 falls n gerade.

Somit ist die Teilreihe mit 1/n harmonisch und somit divergent.

Die Teilreihe mit 1/n^2 ist eindeutig konvergent.

was gilt nun für die gesamte Reihe?

Soweit ich weiß ist eine Folge eine spezielle Funktion mit der Definitionsmenge der natürlichen Zahlen, der Graph besteht also aus Punkten.

Soweit ich dass jetzt verstanden habe werden bei einer Reihe alle Folgenglieder aufaddiert * , also wäre eine Reihe ja letztlich nur eine einzige Zahl.

also: Glied 1 einer Folge + (Glied1+Glied2) + (Glied1+Glied2+Glied3)...

Stimmt das?

und warum injektiv wenn sie linksinvertierbar ist?

..eurer Meinung nach?

Hallo liebe Community, als Hausaufgaben sollen wir folgende Aufgabe erledigen: Wenn ein Becherglas in Rotation versetzt wird, dann drückt sich die Flüssigkeit am Rand Rand hoch und es bildet sich ein Paraboloid aus. Die Gleichung lautet: f (x)=0.5x^2+2. Bestimmen Sie das Volumen des Wassers im Becherglas. Wie hoch stand das Wasser im Becherglas im Ruhestand. Nun haben wir noch folgenden Tipp bekommen: Die Integralfunktion für das Rotationsvolumen gilt nur für die Rotation um die x-Achse. Deshalb muss man die Umkehrfunktion zur quadratischen Funktion finden. Bestimmung der Umkehrfunktion zu y=ax^2+b. 1. Gleichung nach x auflösen: x=(y/a-b/a)^1/2 und als zweites tauscht man die Variablen x und y aus. Kommen wir nun zum meinem Lösungsansatz. Bei der ersten Fragestellung hätte ich gesagt, dass man nun die Gleichung, die man erhält, wenn man y und x umtauscht in die Gleichung die man hat, wenn ein Rotationskörper um die x-Achse rotiert. Also pi mal das Integral von (f (x))^2 dx. Macht das Sinn? Bei der zweiten Fragestellung habe ich leider keinen Ansatz. Ich hoffe meine Frage ist auf Grund der Schreibweise der Formeln trotzdem einigermaßen klar. Danke schon einmal im Voraus!

Ich komme leider nicht weiter.. ich brauche die Nullstellen von f‘(x) = 0,25e^(0,25x) - e^(0,5x)
Ich habe bereits durch 0,25 und 0,5 geteilt und es bleibt e^(0,25x) - e^(0,5x) = 0
Ich weiss nicht wie man das löst mit dem ln..bzw ich verstehe es einfach nicht.

Wie ist die erste Ableitung von dieser Funktion und wie vereinfacht man diese dann? Ich verstehe das absolut nicht...
f(x)=-x-2+e^(0,5x)

Kann mir jemand helfen? Ich habe hatte die Aufgabe Extremstellen der Funktion
f(x)=2xe^x zu berechnen.
Nur leider scheiterts bei mir bei der Produktregel. Ich habe die erste Ableitung bereits unzwar
f‘(x)=2e^x(x+1)
Ich bin nun bei der Zweiten aber weiss leider nicht wie ich das richtig zusammenfassen und ausklammern soll. f‘‘(x)=e^x • (x+1) + 2e^x • 1

Kann mir das jemand erklären?

Gegeben ist eine Schar von Funktionen fa mit der Gleichung fa= -1/3x^3+x^2+a×x. Berechnen Sie den Wert von a für den Fall,dass die Tagente im Wendepunkt an den Graphen von fa die x-Achse unter einem Winkel von 60 Grad schneidet.

Ich hab das echt lange versucht, aber ich komm einfach nicht auf die Lösung!

Hallo könnt ihr mir bei dieser aufgabe weiter helfen hab wirklich schon alles probiert die aufgabe lautet: beim Weitsprung beschreibt die Flugbahn eine Parabel a) wie weit springt eine Sportlerin (in metern) wenn ihre Sprungparabel mit der Gleichung y=-0, 1xhoch2+0,4x+0,5 beschrieben werden kann (NULLSTELLE) DANKESCHÖN vorraus!

Hey, Ich verzweifle grade ein bisschen an einem "Mathe Problem." Ich brauche die Stammfunktion von 0,5x also die funktion, die abgeleitet 0,5x ergiebt. Dankeschön:)

Stammfunktion von -x hoch 2 gesucht.. vielen dank! Ich verzweifle

Hallo erstmal.

Ich halte heute in 2 Wochen meine PL (S3) in Mathe und in heute einer Woche muss ich meine Dokumentation abgeben. Ich muss nur erstmal die Aufgabe verstehen... Vielleicht kannst du mir ja helfen. :) Diese Informationen und Aufgaben habe ich dazu bekommen.

Das Wachstum zweier Populationen lässt sich durch die Funktion f bzw. g beschreiben. Die Funktion f beschreibt exponentielles, die Funktion g lineares Wachstum. Dabei bezeichnen f(t) bzw. g(t) die Anzahl der Individuen der Populationen zum Zeitpunkt t (t in Jahren).

1. Stelle die Gleichungen für f(t) und g(t) auf, wenn der Anfangsbestand zum Zeitpunkt t = 0 jeweils 1500 Individuen und der Bestand nach zehn Jahren jeweils 2000 Individuen beträgt.

2. Berechne den Zeitpunkt innerhalb der ersten zehn Jahre, bei dem der Unterschied zwischen linearem Wachstum und exponentiellem Wachstum am größten ist.

3. Bestimme näherungsweise den Zeitpunkt, an dem eine Population doppelt so viele Individuen hat wie die andere.

Damit du jetzt nicht denkst, ich würde die ganze Arbeit von mir schieben! Meine Ansätze:

Formel für lineares Wachstum: B(t)= p x t + B(0) und exponentielles Wachstum: B(t)= B(0) x a^t

B(0) ist der Anfangsbestand, also 1500 Individuen; p ist die Änderungsrate; t ist die Zeit, hier in Jahren, a ist der Wachstumsfaktor (a=1+p)

Für Aufgabe 1: 2000 - 1500 = 500 also 500 : 10 Jahre = 50 pro Jahr. 50 ist für das lineare Wachstum also die Änderungsrate (p)

Damit kann ich die Gleichung aufstellen: B(10)= 50 x 10 + 1500 = 2000

Für das exponentiellen Wachstum: Zuerst muss ich nach a auflösen.

Allgemeine Formel zum auflösen von a:

B(t) = B(0) x a^t -> durch B(0)

B(t)/B(0) = a^t

t Wurzel von (B(t)/B(0) = a

Für meine Aufgabe:

g(10)= 1500 x a^10 -> durch 1500

g(10)/1500 = a^10 -> die 10. Wurzel von a

1. Wurzel von g(10)/1500 = a = 1.029186009

Damit komme ich dann auch ungefähr auf 2000 Individuen nach 10 Jahren.

Habe ich bis hier hin alles richtig gemacht? Bei den nächsten beiden Aufgaben bin ich dann gescheitert. Ich weiß nur, dass es sich bei Aufgabe 2 nur um den Intervall [0;10] handelt und ich denke ich muss die Differenz berechnen mit einer senkrechten Geraden, wenn ja: Wie finde ich heraus, wo ? Bei Aufgabe 3 denke ich wegen "Bestimme näherungsweise.." daran x gegen einen Wert zu stellen. Außerdem habe ich mir die Graphen mit den Daten aufgemalt und das heißt g(t) =1/2 f(t), da g(t) deutlich schneller ansteigt als f(t).

Ich weiß, dass war jetzt echt viel Text, aber ich hoffe Ich könnte wenigstens schon mal einen Teil klären.

Schreibe demnächst eine Arbeit und es hieß es kommt nur Analysis 1 dran^^

ich versteh die folgende aufgab nicht:# berechnen sie die Steigung der Funktion f im Punkt p

f(x) = x + 32/x, P (4/12)

Ich habe mir bei einer Matheaufgabe diese Frage gestellt.

Ich verstehe nicht wie man in der 4. Aufgabe die Nullstellen bestimmt, kann mir das bitte jemand mit Zwischenschritten erklären?

Hallo, ich bin gerade dabei meine Schulmathematikreste zusammen zu kratzen, aber die Extremwerteaufgaben verstehe ich leider nicht mehr. Aufgabe: U f(×)=x^2-3x+3 P(0/0) An welchem Punkt von f ist der Abstand zu P minimal? Ich habe die beiden jetzt in die Abstandsformel eingesetzt und in Abhängigkeit von u gestellt. Da kam ich dann auf d(u)= Wurzel u^2+(u^2-3u+3)^3 Für u müsste ich jetzt ja jeden beliebigen Wert einsetzten können, um den Abstand von P zu bekommen, oder? Aber wie bekomme ich denn jetzt den richtigen Punkt heraus(also den mit dem minimalsten Abstand zu P) ? Mit herumprobieren wäre man da ja ne Weile beschäftigt... Oder geht das irgendwie mit dem Taschenrechner? Ich habe einen Casio fx-991DE Plus.

Danke im voraus:)

Ich bin verwirrt. Ich verstehe nicht wie man auf diese Ergebnisse kommt. Ich habe eine Funktion gegeben. Und bereits Tangenten und Normalengleichung am Punkt P(2/f(2)).
Die Frage ist jetzt welche Normale an K ist parallel zur y-Achse?

Bei der Lösung verstehe ich nicht woher und wie msn auf die x = 1,5 kommt und y = 4,5? Oder woher man überhaupt weiss wo der Scheitelpunkt liegt?