Mathematik Konvergenz Frage?
Hey , kann mir jemand sagen wie man die Folge auf Konvergenz untersucht? Die Sache, die ich nicht verstehe: ist die Folge überhaupt konvergent und wenn ja, was ist ihr Grenzwert?
Lg und Danke im Voraus
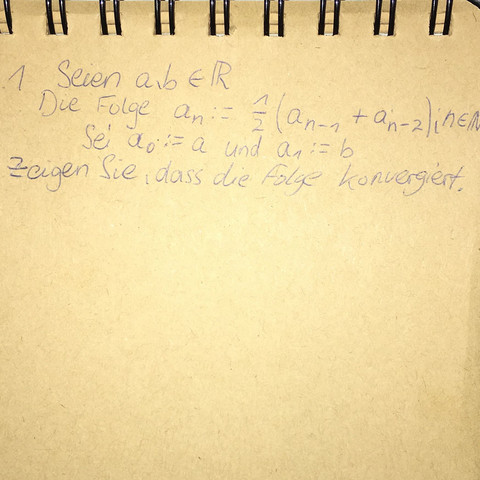
5 Antworten
Zerlege a_n in zwei Teilfolgen mit geraden und ungeraden Folgengliedern und zeige, dass die beide gegen die Grenzwerte g und u konvergieren. Dann ist 2g = 2lim a_{2n} = lim a_{2n-1}+a_{2n-2} = lim a_{2n-1} + lim a_{2n-2} = u+g und folglich g = u. Somit konvergiert deine Folge ebenfalls gegen diesen Wert.
ist die Folge überhaupt konvergent?
Ja.
und wenn ja, was ist ihr Grenzwert?
Konvergiert gegen a.
Der Grenzwert liegt bei (2a+b)/3. Für a=b ist a also doch der Grenzwert :-P
ist die Folge überhaupt konvergent
Benachbarte Folgenglieder haben immer die Differenz
- | aₙ₊₁ - aₙ | = | b - a | / 2ⁿ
Damit hast Du
- ∀k: | aₙ₊ₖ - aₙ | < | b - a | / 2ⁿ⁻¹
Das ist Dein roter Teppich zum Cauchy-Kriterium.
was ist ihr Grenzwert?
Danach wird ja eigentlich nicht gefragt. Aber was soll's: Das Vorzeichen der obigen Differenzen alterniert:
- aₙ₊₁ - aₙ = (b-a) / (-2)ⁿ
Schreibe die Folge aₙ als Reihe
- aₙ₊₁ = a + Σ (aₙ₊₁ - aₙ) = a + (b-a) Σ (-2)⁻ⁿ.
und nutze
- S := 1 - ½ + ¼ - ⅛ + … = Σ (-2)⁻ⁿ = ⅔ (wegen S+S/2=1)
Der Rest ist einfach!
Die Folge konvergiert. Der Grenzwert ist (a+2b)/3.
Hier habe ich einen recht ausführlichen Beweis aufgeschrieben, dass die Folge konvergiert. [Siehe: Seite 1 und Seite 2]
https://www.dropbox.com/s/dt029vdw5a8xtpn/Folgengrenzwert.pdf?dl=0
Auf den Seiten 3 und 4 habe ich eine explizite Formel für die Folge berechnet und den Grenzwert der Folge berechnet.
Anstatt den Konvergenzbeweis wie auf den Seiten 1 und 2 beschrieben mit Cauchy-Kriterium durchzuführen. Kann man natürlich auch sofort eine explizite Formel herleiten, und dann anhand der expliziten Formel nachweisen, dass der Grenzwert existiert.
Letztendlich habe ich dann das folgende Ergebnis erhalten:
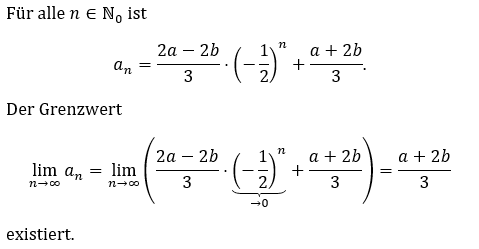
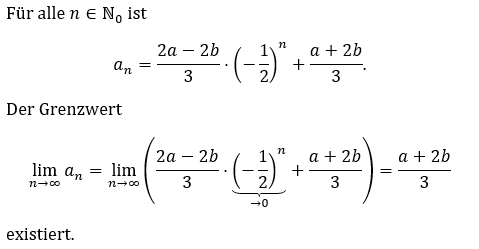
Der Grenzwert liegt irgendwo zwischen a und b (a ist es nicht), wirklich berechnen kann man den vermutlich nicht.
Wenn man Konvergenz zeigen möchte, ohne den Grenzwert zu kennen, bleibt eigentlich nur noch das Cauchy-Kriterium übrig. Veruch es mal damit.
Korrektur: a ist nicht der Grenzwert.