Lineares Gleichungssystem mit drei Unbekannten; Schaffe es nicht zu lösen?
Hallo!
Leider habe ich eine etwas knifflige Aufgabe vor mir. Es geht um das Stoßprozess zweier Teilchen und ich muss den Winkel des ersten Teilchens nach dem Stoß und die jeweiligen Geschwindigkeiten rausfinden.
Ich habe jetzt ein lineares Gleichungssystem erstellt mit den drei Variablen. Nur blöderweise kann ich das LGS nicht lösen!
Ich wäre euch sehr dankbar, wenn ihr mir helfen würdet.
Danke!
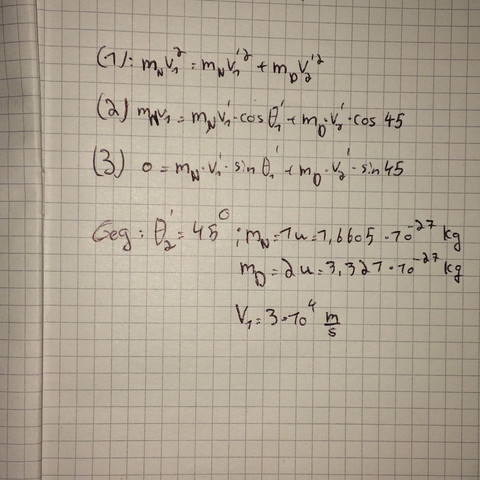
3 Antworten
Ich befürchte, gesucht sind v₁', v₂' und 𝜃₁'. Dann ist das System nicht linear: es enthält Quadrate, Produkte und trigonometrische Funktionen über diesen Variablen.
Falls ich mich nicht verhauen habe, findest Du so eine Lösung (ich schreibe N und D statt m_N und m_D):
aus (3):
- (3.1): v₂' = √2 N/D v₁' sin 𝜃₁'
(2) minus (3) nach v₁' auflösen:
- (2.1): v₁' = v₁ / (cos 𝜃₁' - sin 𝜃₁')
Bemerkung: cos 𝜃₁' ≠ sin 𝜃₁', da sonst Widerspruch zwischen (2) und (3).
(3.1) und (2.1) in (1) einsetzen:
N·v₁² = N·v₁²/(cos 𝜃₁' - sin 𝜃₁')² + 2N²/D·v₁²·sin² 𝜃₁' / (cos 𝜃₁' - sin 𝜃₁')²
⇔ -cos 𝜃₁' = N/D·sin 𝜃₁'
⇔ tan 𝜃₁' = -D/N
Das gibt 2 Lösungen für 𝜃₁'. Für jede kannst Du v₁' aus (2.1) und v₂' aus (3.1) bestimmen und die Werte zur Sicherheit in (1) prüfen. Aber ich denke, dass ich nur Äquivalenzumformungen gemacht habe. Deshalb sollten beide Lösungen passen.
Vermutlich werden die Lösungen (𝜃₁', v₁', v₂') und (𝜃₁'+π, -v₁', -v₂') lauten, was in der Praxis wohl aufs selbe hinausläuft (negative Geschwindigkeit in Gegenrichtung).
nur Äquivalenzumformungen
wie peinlich: kurz vor Schluss habe ich leichtsinnig durch sin 𝜃₁' dividiert. Dabei sind mir Lösungen verlorengegangen: 𝜃₁'=0+kπ, v₁'=±v¹, v₂'=0
Und auch die finale Division durch cos 𝜃₁' muss man noch getrennt untersuchen (liefert aber keine weiteren Lösungen).
Lesen kann ich es nicht.
Aber man hat nicht viele Chancen, wenn man sich um das Additionsverfahren (oder ein ähnliches) herumdrückt.
Empfehlung: Speck die Gleichungen ab. Keine Indizes mehr! Alles reduzieren auf einfache Namen (du kannst ja hinterher zurückbenennen).
Bei dreizeiligen LGS musst du erst I mit II sowie I mit III so zusammenfügen, dass du eine Unbekannte eliminierst. Aus den entstehenden 2 Gleichungen schmeißt du die zweite Unbekannte raus. Und danach ist dann alles klar.
Wenn du die LGS abgespeckt hier hereinstellst, zeige ich es dir an deinem Beispiel.
Eintippen! Nicht fotografieren!
siehe Mathe-Formelbuch "lineares Gleichungssystem" (LGS)
Das Bild kann ich nicht laden,weil mein Datenvolumen verbrauchst ist und die Zahlen und Buchstaben kann ist so nicht lösen.
Am einfachsten geht das mit einen Graphikrechner,(GTR,Casio),wie ich einen habe.
Zahlenbeispiel: x=1 und y=2 und z=3 LGS ist
1) 2*x-3*y+4*z=8
2) 1*x+4*y-10*z=-21
3) -2*x+6*y+7*z=31
Lösung nach den Verfahren:
1) "Additionsverfahren"
2) "Einsetzverfahren"
3) "Gleichsetzverfahren"
4) "Gaußscher Algorithmus"
Hinweis: Die Lösung kennst du ja und so kannst du jeden deiner Rechenschritte auf Richtigkeit kontrollieren.