Ganzrationale Funktionen bestimmen - HILFE?
Ich sitze schon seit 2 Stunden an der Aufgabe und brauche sie für morgen, kann mir eventuell jemand helfen?
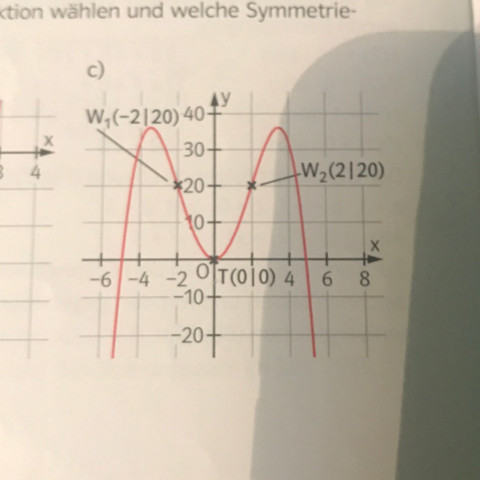
Aufgabenstellung: Bestimmen Sie zu den abgebildeten Graphen jeweils eine mögliche Funktionsgleichung. Überlegen Sie zunächst, welchen Ansatz Sie für die Funktion wählen und welche Symmetrieeigenschaften Sie ausnutzen können.
2 Antworten
Der Graph ist symmetrisch zur Y Achse und damit gilt:
f(x) = f(-x)
ax^4+bx^3+cx^2+dx+e = a*(-x)^4+b*(-x)^3+c*(-x)^2+d*(-x)+e
ax^4+bx^3+cx^2+dx+e = ax^4-bx^3+cx^2- dx + e
2bx^3+2dx = 0 für b = 0 und d = 0 gilt = 0
Daher: f(x) = ax^4+cx^2+e
Gesucht sind also 3 Bedingungen:
Kommst du jetzt weiter?
Vergiss nicht hat f einen Wendepunkt so hast du gleich mehrere Informationen gegeben.
Man sieht ja schon, dass es eine achsensymmetrische Funktion 4. Grades ist, alsogelten muss.
Das heißt man braucht drei Bedingungen, um die Parameter herauszufinden.
Mit dem Wendepunkt bei (2|20) und dem Tiefpunkt bei (0|0) hätte man sogar vier.
"hätte man sogar vier."
Jain, f'(0)=0 ist keine neue Information, das ist schon durch die Achsensymmetrie gegeben.