Bernoulli – die meistgelesenen Beiträge

Hallo,

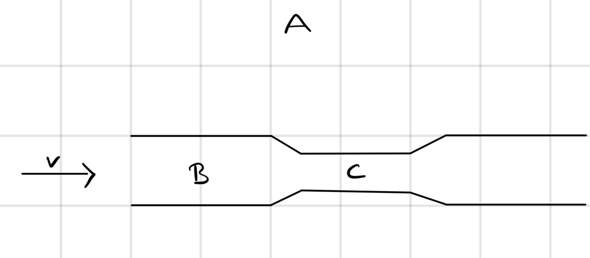
ich versuche eine Erklärung zu diesem Thema zu finden und frage mich wieso der Druck an Stelle A am größten sein soll.

Die Bernoulli-Gleichung unterscheidet in diesem Fall zwischen zwei Druckarten. Einmal dem statischen und dem dynamischen Druck.

An Stelle B müsste aufgrund des hohen Volumen der größte statische Druck herrschen.

Ich frage, wieso Stelle A richtig sein soll, denn schließlich gilt die Bernoulli-Gleichung nur für strömende Fluide in einem Rohr.

"Die Gleichung gilt so nur für Strömungen in Rohren!^[2] Wenn es keine Wand gibt, dann kann sich der Druck an die Umgebung anpassen.^[3] Viele Beispiele für falsche Anwendung der Bernoulli-Gleichung beruhen auf Missachtung dieser Voraussetzung. Eine Wand ist nur dann nicht erforderlich, wenn die Strömung durch ein passives Hindernis umgelenkt wird: Dann kommt es lokal zu Druck- und Geschwindigkeitsänderungen, die der Bernoulli-Gleichung gehorchen"(Quelle:https://sedl.at/Bernoulli-Gleichung)

Komme bei dieser Aufgabe nicht weiter:

eine Münze wird sechsmal geworfen. Mit welcher Wahrscheinlichkeit fallen folgende Ereignisse?

1) genau dreimal wappen

2) weniger als dreimal wappen

3) mehr als dreimal wappen

habe angefangen ein baumdiagramm zu machen, aber schnell gemerkt, dass dies zu groß sei, was soll ich stattdessen tun?

Liebe User, ich habe ein Problem bei meinen Mathe Hausaufgaben und komme nicht weiter. Wir behandeln im Moment Stochastik, Bernoulli-Ketten und Binomialverteilung. Kann mir jemand einen Lösungsansatz für die Aufgabe 2 im Bild geben? Liebe Grüße, eure Maren

Guten Abend, folgende Bernoulli Aufgabe: Auf einer Baustelle werden Klemmen benötigt. Diese sind in Schachteln zu 50 Stück abgepackt und die Wahrscheinlichkeit, dass eine Klemme brauchbar ist, beträgt 90%. Fehlerhafte Klemmen werden weggeworfen und gelten als verbraucht.

1.) Eine angefangene Packung enthält noch 24 Klemmen und es werden genau 20 Klemmen benötigt. Berechnen Sie die Wahrscheinlichkeit P(E1), dass die Packung komplett aufgebraucht wird.

Mein Ansatz: Es gilt: B(n/k/p), sprich B(24/4/0,1)

Meines Wissens nach, müsste ich nun im Tafelwerk die Seite suchen, bei der gilt p=0,1, n=24 sowie k=4, das Ergebniss lässt sich einfach ablesen.

Jedoch folgendes Problem: p=0,1 finde ich, k=4 auch. Jedoch kommt im Tafelwerk n=24 nicht vor. Lediglich 20 und 25 (siehe Foto).

Was mache ich falsch?

Trefferwahrscheinlichkeit 12% Versuche: 10

Bitte unbedingt mit Rechenweg und nicht einfach so die Lösung hinschreiben

Hi,

ich sitze gerade an einer Aufgabe zur Bernoulli-Kette und kenne soweit auch den Rechenweg (sofern richtig), die Aufgabe samst Lösungsweg möchte ich präsentieren, bevor ich zur Erläuterung meiner Frage komme:

Aufgabe: Die Mitglieder der deutschen Tischtennis-Nationalmannschaft gewinnen gegen chinesische Spitzenspieler 15% der Spiele. Mit welcher Wahrscheinlichkeit gewinnen die Deutschen von 10 Einzelspielen mehr als 2?

p=0,15; n=10, k=2, k=3, k=4, ..., k=10

Nun würde ich normal die Rechnungen mit den verschiedenen Anzahlen an Treffern k addieren, sprich

P(x>2) = (10 über 2)0,15^2(1-0,15)^10-2 + (10 über 3)0,15^3(1-0,15)^10-3 + ...

Da k allerdings für mich optisch nichts anderes als 10! ist, nur eben, dass jeder neue Wert einzeln berücksichtigt wird, frage ich mich, ob man die Rechnung nicht abkürzen kann, damit man nicht neun Teilrechnungen hat oder in anderen Fällen vielleicht sogar noch mehr.

Heyyy,

ich habe in Mathe eine Hausaufgaben, welche ich leider so gut wie gar nicht verstehe. Vielleicht kann mir jemand von euch einen Anstoß geben:

51,4% aller Neugeborenen sind Knaben. Eine Familie hat sechs Kinder. Wie groß ist die Wahrscheinlichkeit, dass es genau drei Knaben und drei Mädchen sind?

Vielen Dank für eure Unterstützung, Wahrscheinlichkeiten kann ich wirklich gar nicht :)

Habt ihr eib schlüssiges Beispiel für die komplette berechnung eine Problems und wie gibt man beispielsweise 5 über 2 auf einem taschenrechner ein?

2. Ein Flugzeug hat 174 Plätze. Die Fluggesellschaft verkauft 179 Tickets, weil nicht alle Gäste, die gebucht haben, zum Flug erscheinen. Mit höchstens 1 %iger Wahrscheinlichkeit muss die Fluggesellschaft mehr als zwei Fluggästen eine Entschädigung bezahlen, weil ihr gebuchter Platz nicht verfügbar ist. Wie groß ist der Anteil der Gäste, die gebucht haben und zum Flug erscheinen, höchstens?

Mein Ansatz hier:

p ist gesucht

X: Anzahl erscheinender Gäste

n=179

P<=0,01

k>176

Wie könnte man hier jetzt weiter rechnen?

Man kann von einer Wahrscheinlichkeit von 1/3 von einer Infektion ausgehen.

Um valide Ergebnisse bei Studien zu erhalten, benötigt man ausreichend infizierte Personen.

Ermitteln Sie, wie viele Teilnehmer*innen mindestens befragt werden müssten, damit mit einer Wahrscheinlichkeit von mindestens 95% mindestens 200 Infizierte dabei sind?

Berechne die Werte der einfachen Binomialverteilung im TR

B(10;0,5;6)

B(10;0,75;3)

B(20;0,25;7)

B(8;0,1;2)

Wie gebe ich das in meinen Taschenrechner ein? Habe einen Casio fx-991DEX. Ich weiß leider nur, wie man es kummuliert im TR eingibt. 

Bei einer Fluglinie erscheinen durchschnittlich 95 % der Passagiere, die gebucht haben, zum Flug. Ein Flugzeug hat 174 Plätze. Die Fluggesellschaft möchte so viele Tickets verkaufen, das mit höchstens einprozentiger Wahrscheinlichkeit mehr als zwei Fluggäste wegen eines nicht vorhanden. Sitzplatz ist trotz Buchung entschädigt werden müssen. Wie viele Tickets auf die Fluggesellschaft höchstens verkaufen?

Meine Ansätze:

n ist gesucht

X: Anzahl erscheinender Fluggäste 

p=0,95

k=>177

P=<0,01

Ergeben diese Ansätze Sinn und wie könnte ich bei dieser Aufgabe vorgehen?

In meinem Mathematikbuch steht folgende Aufgabe: Der Wochenspiegel ist eine kostenlose Werbezeitung mit einer Auflage von 5000 Exemplaren. In 80% aller Haushalte wandert sie ungeöffnet in die Mülltonne.[Frage in der Überschrift].

Ich hatte gedacht, dass es sich hierbei um eine binomialverteilte Wahrscheinlichkeit handelt mit dem Parameter n = 5000 und der Trefferwahrscheinlichkeit p = 0,2. Mein Ansatz ist in dem von mir beigelegtem Bild, welcher handelsüblicher Taschenrechner jedoch kann denn die Fakultät von 5000 berechnen?

Gibt's da irgendwie einen anderen Lösungsweg? In den Lösungen steht nämlich leider nur das Ergebnis, 24,6%. Wenn ihr mir helfen könnt, wäre ich euch sehr verbunden.

wenn ich die wahrscheinlichkeit von einem ereignis oder die wahrscheinlichkeit eines anderen ereignises berechen soll und beides steht in einer aufgabe bzw satz ist dann das ergebnis die vereinigung der beiden lösungen ?

Bin bei Wahrscheinlichkeit bei den Bernoulli Ketten und weiß nicht mehr wie man das eintippt kann mir bitte jemand helfen

Diese Aufgabe ist über Laplace zu lösen. Ich verstehe jedoch nicht, wieso mal die Wiederholung zu berücksichtigen ist und mal nicht.

Wer kann mir das erklären?

Hallo,

wie löse ich folgenden Aufgabentyp, illustriert anhand anschließenden Beispielen:

1.Wie oft musst du eine Münze mindestens werfen, um mit einer Wahrscheinlichkeit von mindestens 95% mindestens 4-mal "Zahl" zu werfen?

2.Eine neue Diät soll erprobt werden. Dabei dürfen in einer Stichprobe von 80 Frauen mit einer Mindestwahrscheinlichkeit von 95% maximal 6 Frauen mit erhöhtem Blutdruck sein. Wie hoch darf bei der Anmeldung zur Diät-Erprobung der Prozentsatz der Frauen mit erhöhtem Blutdruck maximal sein?

Viele Grüße und danke im vorraus!

Hallo,

ich haben mir gerade im Internet ein Video zur Formel von Bernoulli angesehen und es soweit verstand. Jetzt habe ich aber eine Aufgabe und es sieht ganz anders aus als in den Beispielen im Internet. Hier wurden die Wahrscheinlichkeiten eine 6 zu würfeln als Bruch geschrieben oder?

Aus dem Internet. 5 Torschüsse, 2 Treffer

Ist das genauso wie oben nur mit Brüchen geschrieben?

Hey, ich hab ein Problem mit folgender Aufgabe aus dem Lambacher Schweizer 12. Klass Buch: Für eine Sorte von Blumenzwiebeln gibt es eine Keimgarantie von 90%. a) In einer Packung sind 20 Zwiebeln. Mit welcher Wahrscheinlichkeit keimen mindestens 16 Zwiebeln (höchstens 14 Zwiebeln; alle 20 Zwiebeln). b) Ein Hausbesitzer möchte, dass mit mindestens 95% Wahrscheinlichkeit wenigstens 12 Blumen in seiner Rabatte blühen. Begründen Sie, dass er mindestens 16 Blumenzwiebeln pflanzen muss.

Ich muss über diese Aufgabe ein Referat halten, heißt möglichst detailliert erklären. Nun hab ich mit der Aufgabe allerdings Verständnisprobleme. Ich weiß, dass bei a) n=20 und p=0,9. Ich weiß allerdings nicht, wie man "mindestens" bzw. "höchstens" Wahrscheinlichkeiten berechnet. Das gleiche Problem habe ich auch mit Teilaufgabe b).

Wir haben das Thema erst angefangen, und unser Leher hat gleich Referate dazu verteilt. Zeit, um nachzufragen und Verständnisschwierigkeiten zu lösen gab es keine. Ich hoffe wirklich ihr könnt mir hier helfen. Vielen Dank schon mal im voraus!

-Samuel

Ich habe eben meine Stochastik Prüfung gehabt und die erste Aufgabe war:

Wir werfen einen Würfel 4mal. Wir addieren alle Würfe wobei wir einmal die größte und die kleinste geworfene Zahl abziehen von der Summe. Berechnen Sie die Wahrscheinlichkeit eine Augensumme größer als 10 zu erhalten.

Ich habe so ein bisschen vor mich hingerechnet und mir paar Dinge überlegt. Aber das war eher so ein bisschen "ich mach jetzt was und hoffe es ist richtig". Mein Ergebniss war 12/60 = 1/5.

Vllt kann mir ja jemand mal erklären wie man hier zu einer schönen Lösung kommt. Vielen Dank schonmal im voraus

Hallo, ich wollte mal nach dem Unterschied vom Zusammenhang des Binomialkoeffizienten und der Bernoulli Formel. Der Binomialkoeffizient gibt doch an, dass ein Experiment ohne Zurücklegen geschieht. Dieser ist jedoch auch bei der Bernoulli Formel enthalten. Das Bernoulli Experiment ist jedoch dafür bekannt, dass es mit Zurücklegen ist, 2 Ausgänge und ohne Reihenfolge. Wieso ist es trotzdem in der Formel enthalten.

Wäre dankbar für Antworten😊

Ich bräuchte einmal Hilfe bei folgender Aufgabe:

"In einer Urne befinden sich 3 rote und 7 weiße Kugeln.

Zweimal nacheinander wird jeweils eine Kugel zufällig entnommen und wieder zurückgelegt. Berechne die Wahrscheinlichkeit dafür, dass höchstens eine der entnommenen Kugeln weiß ist."

Bräuchte einmal einfach nur einmal Rechenweg mit Lösung.

Vielen Dank im Vorraus

Hallo zusammen, zu aller erst ich weiß dass das hier keine Hausafgaben Hilfe oder sonstiges ist, ich bitte nur um Hilfe da ich überhaupt nicht weiter weiß und nicht darum dass mir jemand die komplette Lösung sagt :)

Meine Aufgabe: Wie viele Deutsche muss man mindestens zufällig auswählen, um mit mindestens 99,99% Wahrscheinlichkeit mindestens einen Mann gewählt zu haben? Das Verhältnis der männlichen zur weiblichen Bevölkerung beträgt zurzeit 0,96 zu 1.

Was ich verstanden habe ist, dass die 99,99% meine Wahrscheinlichkeit sind, und das "mindestens ein Mann" mein k. Aber was genau ist das p bzw. n und welches muss ich dann berechnen?

Hallo,

da meine Schulzeit schon viele Jahre zurückliegt, habe ich - wie es scheint - leider die einfachsten Stochastik-Basics vergessen :-(

Könnte mir evtl. bitte jemand bei folgender Aufgabe helfen?

Wenn man eine Münze n mal wirft (sagen wir 10) und mindestens k mal (sagen wir 7) eine bestimmte Seite möchte (sagen wir Zahl), wie rechnet man dann die Wahrscheinlichkeit dafür aus?

Es müsste ja irgendwie so gehen, dass man von 1 den Wert für 6 mal oder weniger subtrahiert, oder? Aber wie kommte ich denn dann auf die Wahrscheinlichkeit für 6 mal oder weniger?

Ich hoffe man versteht, was ich meine, und dass ich die Buchstaben korrekt benutze.

Freue mich über jede Hilfe :-)

Ich check einfach nicht wann was verwendet wird. Klar Bernoulli ist mit Zurücklegen und Lottomodell ohne. Das hilft mir auch net weiter

Hey,

Ich verstehe gerade nicht was ich falsch mache und zwar lautet die Aufgabe:

Das Glücksrad wird sechsmal gedreht.Wie groß ist die Wahrscheinlichkeit, dass höchsten 2 mal grün erscheint.

Die Grüne Fläche nimmt 3/4 ein und die orange 1/4

Ich habe folgendes berechnet

1-P(X=3)=0,868164 jedoch steht in der Lösung dass es 0.0376 ergeben muss.

Was habe ich falsch gemacht?

Wie wahrscheinlich ist es das man mindestens 1 mal Zahl würfst.

Ich habe zu den beiden unten markierten Aufgaben eine Frage.
1) Wie soll ich bei nicht kumulierten Wahrscheinlichkeiten eine Schätzung machen? Ich habe da leider garkeine Ahnung wie ich vorgehen muss
2) Ich hätte die Wahrscheinlichkeit auf 50% getippt, weil der Erwartungswert 10 ist und alle Werte links daneben sind bei p=0,5 ja die Hälfte. Die Lösungen sagen aber 58,81%?

Ich habe mir eine Aufgabe angesehen, und ich versteh halt gar nicht, wie ich K im Taschenrechner eingebe.

Ich weiß n über k, aber welche Tastenkombi muss ich für K drücken? Ich finde da nichts in der Anleitung, was mir schlüssig klingt.

Hallo, ich muss für einen Mathe Test lernen und wir behandeln zurzeit das lotto Modell. Dabei bin ich zu dieser Aufgabe gekommen, jedoch weiß ich nicht wie ich sie lösen soll (Aufgabe 2d)

Hallo, ich lerne gerade für meine Mathearbeit und habe mal eine Frage. Ist meine Lösung zu der folgenden Aufgabe richtig?
Ein idealer Würfel wird zehn mal geworfen, wie hoch ist die Wahrscheinlichkeit, dass genau vier Sechsen dabei rauskommen?

Folgendes Bild ist meine Lösung:

In einem Kinderparadies steht eine große Kiste mit 15 goldenen, 20 roten und 25 blauen

Ballen, aus der die Kinder mit geschlossenen Augen einen Ball herausgreifen dürfen. Anschließend wird er wieder zurückgelegt. Wenn ein Kind zum dritten Mal einen goldenen Ball gezogen hat, darf es ihn behalten.

Wie oft muss es wohl ziehen, um mit mehr als 50 %iger Wahrscheinlichkeit einen goldenen Ball behalten zu können?

Meine Ansätze:

n ist gesucht

k=3

p=0,25

P>0,5

Also:

P(x=3)>0,5

Mein Problem jetzt: Für kein eingesetztes n erhalte ich eine Wahrscheinlichkeit von über 50%

Danke im Voraus!

Bei der Stochastik gibt es ja den bernoulli versuch mit dem man wahrscheinlichkeiten berechnen kann. wann benutzt man aber die punktwahrscheinlichkeit bzw. die inervallwahrscheinlichkeit, und wann die bernoulli formel? danke

Eine Münze wird n=100 mal geworfen. X sei die Anzahl der kopfwürfe. Berechne die Wahrscheinlichkeit dass X in einer 2 Sigma Umgebung des Erwartungswerts liegt. Bestätigt das Ergebnis die 95,5 % Sigmaregel angenähert?

Kann mir bitte einer erklären wie ich bei dieser Aufgabe vorgehen soll?? ich bin voll am strugglen

Hallo,

hab die Aufgabe erfolgreich bis zur c) durchgerechnet. Bei der c) und d) ging es dann nicht mehr. Lösungen vorhanden aber ohne einen ausführlichen Weg. Kann mir da jemand helfen?
Aufgabe 5

Hallo, ich komme bei der Aufgabe 5 nicht weiter… Meine Lehrerin hat uns die Formel 1-P(X<k) vorgegeben, jedoch weiß ich nicht was ich für k einsetzen soll.
Wäre über Lösungsansätze dankbar :)

Meiner Meinung nach ist die Antwort in der a) falsch bzw. so grob formuliert, dass man sagen könnte, dass sie falsch ist. Weil die, die dort nicht gehen haben auch keine 94% Wahrscheinlichkeit auf einen Platz am Flughafen. Das heißt nur die, die dort ihr Ticket später einlösen möchten haben eine 94% Wahrscheinlichkeit auf einen Platz. Da aber niemand weiß, ob er zu den 90 % gehört, die dort tatsächlich auch ankommen zur Ticketeinlösung kann niemand bzw. man kann nicht behaupten, dass jeder eine 94% Wahrscheinlichkeit auf den Platz hat. Nur bei den 100 Ticketkäufer insgesamt kann man sagen, dass da eine 94% Wahrscheinlichkeit für einen Platz bei dieser 100 Mann großen Gruppe besteht besteht.

Könnt ich nachvollziehen, was ich meine...

Das hat mich wirklich beschäftigt.

Guten Tag, ich muss gerade ein Physikreferat vorbereiten und habe als kleines Experiment eine Wasserrakete gebaut. Nun will ich die Flughöhe berechnen und habe dazu eine Anleitung gefunden. Man benötigt für die Berechnung die Geschwindigkeit des ausströmenden Wassers aus der Rakete. Diese soll man mit der Bernoulli-Gleichung berechnen können. Nun verstehe ich aber den letzten Schritt bei der Herleitung der Formel nicht.

Wie kommt man von der Gleichung darauf, dass p + 1/2 * p * v^2 konstant ist?

Sind folgende Experimente Benoullie Experimente?? 1) Reißzwecke werfen 2) Aus Gefäß Lose ziehen, die entweder Nieten oder Gewinnen sind 3)Kugel aus Gefäß ziehen mit roten, grünen und weißen Kugeln --> Darauf achten, ob die gezogene Kugel rot ist 4) Gleichzeitig 2 Münzen werfen und gucken ob die oben liegenden Seiten gleich sind

Sind folgendne Experimente Bernoulli Ketten? 1) Würfel wird sieben mal nach einander geworfen und die Augenzahl wird jeweils notiert 2) Aus einer Urne mit 20 schwarzen und 10 weißen Kugeln werden 12 Kugeln gezogen. Die gezogene Kugel wird jedesmal in die Urne zurückgelegt (nicht zurückgelegt). Gucken, ob die gezogenen Kugel weiß ist.

Wenns geht mit Begründung

Moin,

Wir schreiben demnächst eine Klausur über unter anderen binomialverteilte Wahrscheinlichkeiten.

Ich kenne 3 Möglichkeiten, diese zu berechnen:

Bernulli-Formel: P(x=k)= (n über k) * p^k *...

Taschenrechner: Binomial-Dichte bei (x=...) und Kumul.-Dichte bei (x>/<...)

Summenformel mit Bernulliformel

Wann wende ich welche Methode am besten an?

LG Max

Gibt es hier einen Unterschied oder ist es dasselbe? Mein Lehrer verwendet es Synonym.

Hallo, ich schreibe bald mein Abitur und komme bei folgender Aufgabe nicht weiter ? 

Bei einem Interview werden 20 Schüler befragt ob sie ein Handy besitzen.

a) Berechne die Wahrscheinlichkeit das keiner der Schüler ein Handy hat.

b) Berechne die Wahrscheinlichkeit das mindestens 2 Schüler ein Handy besitzen.

Die Trefferwahrscheinlichkeit beträgt 1/9.

Laut Lösungsbuch kommt bei a 9,48%raus und bei b 66,81%.

Meine Frage wäre wie ich das mit der Bernoulli Formel berechnen kann ?

Ich komme leider nicht auf das richtige Ergebnis? Die Lösung lautet cRohr= 12,91 m/s und meine Lösung lautet cRorhr= 14,35 m/s.

Wäre sehr dankbar, wenn mir jemand sagen könnte, wo ich einen Fehler gemach habe.

Guten Tag,

Ich bräuchte mal Hilfe im Latex Format

Ich möchte n mit 150 ersetzen und k mit 30, aber wenn ich es versuche kommt das dabei raus.

Kennt sich damit jemand gut aus? wäre sehr dankbar.

Hi hat jemand einen Ansatz für D und E?

Deutsche Euro-Münzen werden an funf Standorten geprägt. 21% aller Münzen tragen ein „J", was auf die Prägung in Hamburg hinweist. Ein Erwachsener hat in seiner Geld- börse 46 Münzen. Die Zufallsgröße X zählt die Anzahl der in Hamburg geprägten Münzen in der Geldbörse des Erwachsenen und wird als binomialverteilt angenommen.

d) Eine weitere Prägeanstalt befindet sich in Karlsruhe. Es ist bekannt, dass die Wahrscheinlich- keit, dass sich mindestens 5 Münzen aus Karlsruhe unter den 46 Münzen befinden, 79,04% beträgt. Bestimmen Sie auf Basis dieser Angabe die Wahrscheinlichkeit dafür, dass eine deut- sche Euro-Münze aus Karlsruhe stammt.

e) 2€-Münzen werden von Banken in Rollen von 25 Stück verpackt. Eine dritte Prägeanstalt ist in Stuttgart beheimatet. Es ist bekannt, dass die Wahrscheinlichkeit, dass von 20 Rollen min- ⚫ destens 10 Rollen mindestens 6 Münzen aus Stuttgart enthalten, 82, 17% beträgt. Bestimmen Sie die Wahrscheinlichkeit dafür, dass eine Münze aus Stuttgart stammt.

hab bis jetzt nur für Werte

p =79,04%

n 46

x =5

wenn überhaupt richtig (?)

aber keine Ahnung was ich wie wo einsetzen muss.

Hallo, die Aufgabe lautet:

Das Gewicht von Eiern freilaufender Hühner auf eine, Bauernhof ist normalverteilt mit Erwartungswert E(x)= 55g und Standardabweichung Sigma=5g. Das Gewicht der Eier wird auf volle Gramm-Zahlen gerundet.
Bestimmen Sie die Wahrscheinlichkeit, dass ein beliebig aus diesen Eiern ausgewähltes Ei

(1) mindestens 45g, höchstens 53g;

(2) mindestens 45 g;

(3)höchstens 50g;

(4)genau 60g wiegt.

als Hinweis steht da noch: „Beachten Sie: Das Ergebnis in Teilaudgabe 1 bedeutet, dass das Gewicht mindestens 44,5 g aber weniger als 53,5g beträgt.“

ich würde jetzt denken, dass man da ja keine Stetigkeitskorrektur mit +- 0,5 braucht, da man das ja nur benutzen muss, wenn in der Aufgabe steht, dass es binomialverteilt ist, d.h. man braucht die Stetigkeitskorrektur nur wenn man durch die Normalverteilung die Binomialverteilung annähern will. Also muss man diese Werte einfach in den Taschenrechner ohne Stetigkeitskorrektur eingeben, weshalb dieser Hinweis eigentlich keinen Sinn ergibt.

was ist nun richtig?

Kann mir jemand sagen ob es richtig ist?

Zwei Würfel werden geworfen.

b) Mit welcher Wahrscheinlichkeit treten die folgenden Ereignisse ein? 

Frage: „Augenprodukt < 10“ 

also ich habe so gerechnet : 31/36

Hallo Community,

als Vorbereitung auf die anstehende Mathe-Klausur habe ich nochmal ein paar komplexe Aufgaben durchgerechnet, wobei ich bei einer Aufgabe echt ratlos war:

Es wäre nett, wenn jemand die komplette Aufgabe überprüfen kann und mir mitteilt, wo ich Fehler gemacht habe. Der eigentliche Grund, warum ich diese Frage stelle, ist aber die Aufgabe c). Ich habe zwei verschiedene Ansätze, von denen ich nicht weiß, welcher richtig ist oder ob überhaupt einer der beiden richtig ist.

Es wäre sehr nett, wenn ihr euch diese Aufgabe anschauen könntet und mir sagen könnt, was genau hier zu tun ist.

Vielen Dank!

Grüße und ein schönes Wochenende

carbonpilot01

Ich habe bzgl. folgender Aufgabe eine Frage: Eine verbogene Münze mit der Wahrscheinlichkeit p=0,4 für Zahl wird zehnmal geworfen. Mit welcher Wahrscheinlichkeit fällt

a)in den ersten drei Würfen "Zahl" und in den restlichen "Kopf"?

b) höchstens dreimal "Zahl"

c) in den ersten drei Würfen jedes Mal "Zahl", insgesamt aber viermal "Kopf"

d) in den ersten drei Würfen höchstens einmal "Kopf" und unter den letzten 5 Würfen mindestens zweimal "Kopf"?

Es geht mir nicht um die Lösung, ich brauche den Rechenweg. Ich war leider in den letzten Stunden nicht da, alleine dies nachzulernen hat mich nur noch verwirrter gemacht. Wäre schön, wenn mir jemand helfen könnte. Binomialverteilung hatten wir bisher noch nicht, also fällt dies als Lösungsmöglichkeit weg. DANKESCHÖN im Voraus! :)

Hallo

was ist die Formel für ein duales Urnenmodell bei dem 6 Kugeln auf 3 Urnen verteilet sind, wobei die Kugeln unterscheidbar sind aber die Urnen nicht?

Hi!

Handelt es sich bei diesen Fragen um eine Bernoulli-Kette oder nicht? Am besten mit kurzer Erklärung dazu…

Handelt es sich bei dem Zufallsexperiment um eine Bernoulli-Kette?

1. Fünffaches Werfen einer zerbeulten Münze
2. Das Werfen von fünf verschieden verbeulten Münzen hintereinander
3. Ziehen von fünf Namenskarten aus einer Lostrommel mit Zurücklegen der Karten
4. Fünffaches Setzen auf Rot beim Roulette spielen
5. Ziehen von fünf Namenskarten aus einer Lostrommel ohne Zurücklegen der Karte

Danke im Voraus

Liebe Community,

für Mathe muss ich u.a. zwei Aufgaben lösen, jedoch weiß ich nicht, wie der Ansatz aussieht:

Vignette Wer in der Schweiz die Autobahn gefahren will, muss eine Vignette kaufen, die für das laufende Jahr Gültigkeit besitzt. Die Wahrscheinlichkeit dafür, dass ein Autofahrer noch eine Vignette kaufen muss, sei p.

d) Bei bekannter Wahrscheinlichkeit p=15% beobachtet man einreisende Fahrzeuge so lange, bis man eines ohne Vignette entdeckt, höchstens aber 10 Fahrzeuge. Bestimmen Sie die Wahrscheinlichkeit, dafür, dass tatsächlich 10 Fahrzeuge beobachtet werden müssen.

e) Das Ereignis, dass bei einer Einreise von 10 Fahrzeugen die ersten 4 Fahrzeuge mit Vignetten bestückt sind, aber trotzdem unter den 10 Fahrzeugen genau 2 Fahrzeuge noch eine Vignette benötigen, werde mit B benannt. Bestimmen Sie die Wahrscheinlichkeit P(B) allgemein in Abhängigkeit von p.

Bei der letzten Aufgabe irritiert mich auch "in Abhängigkeit von p". Was kann damit gemeint sein?

Ich vermute, hierfür die Bernoulli-Formel verwenden zu müssen, bin mir jedoch nicht sicher.

Könnt ihr mir dabei helfen, die jeweiligen Ansätzen zu finden und die Problematik mit der Abhängigkeit zu klären?

Vielen Dank im voraus.

Alles Liebe, Kiliara

Binomialverteilung verstehe ich. Aber ich finde keine Aufgabe in meinem Mathebuch zu einem nicht binomial verteilten Zufallsexperiment. Wie könnte so eine Aufgabe aussehen? Gibt es einen anderen Begriff für nicht binomial verteilt?

Hallo liebe Matheprofis,

ich rechne gerade diese Aufgabe:

Bei c) habe ich die Gleichung so in den Taschenrechner eingeben:

Doch leider erhalte ich immer die Meldung „Argumentfehler“. Ich habe mir dann damit beholfen, die Bernoulli-Ketten für k=0 und k=1 manuell einzugeben. Doch dies wird entsprechend aufwendig, wenn k größere Werte annimmt. Weiß jemand warum bei der ersten Gleichung diese Meldung erscheint?

Bei ähnlichen Aufgaben, bei den nach k oder p gefragt ist, habe ich hingegen keine Probleme, wenn ich mit dem gleichen Taschenrechnerbefehl vorgehe.

LG

Hallo,

lerne gerade für meine Klausur. Mein Lehrer meinte, dass das obige Symbol „das Spiel“ ist. Das kann ich aber nicht nachvollziehen. Kann mir das jemand bitte umschreiben? Ich glaube mir fehlt einfach eine richtige Definition, damit ich die Aufgaben besser rechnen kann. So kann ich dann auch mal verstehen, wie man P(X<n) liest.

außerdem: Ich bin in der Q2 NRW auf dem Gymnasium. Vielleicht, weiß ja jemand, was genau ich brauche

Danke im Voraus

Zwei Würfel mit den abgebildeten Netzen werden geworden. Ich habe jetzt diese Tabelle erstellt. Wie erkenne ich in der Tabelle einen Pasch?

Hallo, ich komme bei folgender Aufgabe nicht weiter. Wäre nett, wenn mir da jemand helfen könnte. Danke schonmal im Voraus.

Bei einer Service-Hotline einer großen Firma stehen immer 4 Leute zur Verfügung Ein Gespräch dauert in der Regel ca. 5 Minuten. Pro Tag (Anrufzeiten von 8 - 18 Uhr) rufen etwa 300 Kunden an. Wenn zu viele Kunden bei ihrem Anruf warten müssen, wirkt sich dies negativ auf die Kunden-zufriedenheit aus. a) Wie groß ist die Wahrscheinlichkeit, dass mindestens ein Kunde in der Warteschleife warten muss? b) Lohnt es sich für die Hotline das Personal um eine Person aufzustocken? Tipp: Die Zeiteinheit 10 Stunden wird in 5 Minuteneinheiten eingeteilt. Die Wahrscheinlichkeit, dass in einer Zeiteinheit ein Kunde anruft, betagt dann p= 5/600

(Ich benutze einen GTR)

Kann mir jemand bei der Beantwortung von Aufgabe 13a) helfen ?

Ich hätte gedacht, dass man das mit dem Taschenrechner unter binomcdf(8,3.33,2) berechnen kann, jedoch zeigt dieser mir die ganze Zeit „Error“ an. Habe ich vielleicht die Wahrscheinlichkeit, dass überhaupt gelb fällt (ich habe eins geteilt durch sechs gerechnet, was ungefähr 33.3 ergeben hat) falsch gerechnet, oder was habe ich falsch gemacht ?

Danke im Voraus! :)

Die Zufallsgröße X ist binomialverteilt mit n=60 und p=0.20. Bestimmen Sie, wie groß der Parameter k mindestens sein muss, damit Folgendes gilt:

a) P(X≤ k) ≥0,5

b) P(X≤ k) ≥0,8

c) P(X≥k)≤ 0,2

d P(X ≥ k)≤ 0,4

Wie rechne ich hier k aus?

Ich habe eine Frage zu der 4b: wenn die Wahrscheinlichkeit für Wappen zunimmt, müssten dann nicht auch die Wahrscheinlichkeit für dreimal Wappen und so weiter auch größer werden?

Danke im Voraus

Aus einer Urne mit 15 weißen und 15 schwarzen Kugeln werden blind nacheinander 50 Kugeln mit Zurücklegen entnommen. Wie hoch ist die Wahrscheinlichkeit dass mehr weiße als schwarze Kugeln gezogen werden.

Komme iwie nicht drauf

Hallo,

Ich benötige etwas hilfe bei dieser Aufgabe.

Bei a würd ich gern wissen was mit modellieren gemeint ist

Bei b: muss ich so ein diagramming machen ?

Weil mir kommt es so vor als müsste ich z.b. 375 -90% Rechnung

Und was verstehe ich unter P (X > 360) ~5%

Ist sehr dringend

Wenn ein Flug 100 gebuchte Passagiere hat und im durschnittliche 2 Leute nicht erscheinen. Mit welcher Wahrscheinlichkeit kommen alle 100, bzw. Was ist überhaupt die Wahrscheinlichkeit für das Fehlen von 2 passagieren

Guten Abend an alle,

könnte mir bitte jemand diese Aufgabe erklären?

Normalerweise ist immer p gegeben, aber bei dieser Aufgabe ist es andersrum, man muss p herausfinden.

Den Rechenweg im Buch hatte ich nicht verstanden könnte es bitte jemand für Dummies erklären?

vielen Dank im Voraus

Hallo, leider habe ich Schwierigkeiten diese Aufgabe zur Binomialverteilung zu lösen. Wie müsste man hier denn vorgehen?

Formulieren Sie ein Zufallsexperiment und ein Ereignis, dessen Wahrscheinlichkeit mithilfe des Terms

(15 nCr 4) •0,25⁴ • 0,75¹¹ berechnet werden kann.

LG

Hallo alle zusammen,

Ich brauche mal Hilfe bei Aufgabe 9. Ich weiß nicht was k(=Trefferwahrscheinlichkeit) ist.

Ich freue mich auf eine Antwort.Dankeschön im vorraus

Lg

Hallo, kanm mir jemand bei dieser Aufgabe (Aufg.2) helfen? Ich schreibe heute Klausur und weiß einfach nicht wie man das löst.

Danke im Voraus

Hallo,

ich habe von einem kleinen Experiment gehört:

man nimmt ein DIN A4 Blatt, und hält es ca. 1cm über den Tisch mit den Fingern. Dann pustet man (kräftig) zwischen das Blatt und die Tischplatte.

Man Beobachtet, dass das Blatt recht laut raschelt und mit einer recht hohen Frequenz flattert.

Scheinbar kann man dies mit dem Bernoulli Effekt erklären - ich verstehe jedoch nicht so ganz, wie das funktioniert.

Ich würde mich sehr über eine Antwort freuen!

Zwei Würfel werden geworfen. Die Augenzahlen werden addiert. Ist es wahrscheinlicher, dass die Summe der Augenzahlen kleiner als fünf ist oder dass man zwei gleiche Augenzahlen wirft?

Begründe!

danke schön!

Ich versuche gerade, Aufgabe 12 zu lösen:

a) habe ich gut hinbekommen: 1-P(X<=1) (mit n=5 und p=0,4)

Bei b) allerdings habe weiß ich nicht genau, wie ich vorgehen soll. Das ist ja nicht dasselbe wie P(X=2) (n=5 und p=0,2), da ich ja hier die Reihenfolge beachten muss. Ich könnte auch so rechnen: 1/5 * 4/5 * 4/5 * 4/5 * 1/5, aber da beachte ich ja auch nicht die Reihenfolge wegen dem Kommutativgesetz, außerdem soll ich das wahrscheinlich mit der Bernoulli-Formel ausrechnen.

Bei c) muss man, nehme ich an, so rechnen: P(X<=1) + P(X>=4) (n=5 und p=9,4)

Und bei d) habe ich wieder das gleiche Problem wie bei b).

Ich weiß dass es mit Binomialverteilung gemacht wird, aber ich hab mich gefragt ob es nicht auch mit Normalverteilung geht…

weil man sucht ja einen Wert der genau unter diesen 5% liegt oder über und die obere und untere Schranke würde sich ja auch berechnen lassen

Hallo, suche eine komplette Herleitung der Bernoulli-Formel/Kette, am besten mit Erklärungen. Das was ich im Internet finde ist entweder was anderes oder zu kompliziert. Bitte schnelle Antwort, danke!

Die Wahrscheinlichkeit für die Geburt eines Jungen bzw. eines Mädchens ist ungefähr 0,5. Wie groß wird bei Familien mit 3 Kindern der Anteil?

Also da weiß ich, man muss P(1,2,3..) rechnen und da kam sicherlich 37,5%, 37,5%, 12,5% raus. Aber die darauffolgende Aufgabe versteh ich nicht. Kann wer helfen?

Bestimme die Anteile von Familien mit 0,1,2,3 Mädchen unter den 846000 Familien mit 3 Kindern unter 18 Jahren in Deutschland.

Wie gesagt, ich weiß nicht wie ich das lösen soll, war auch nicht da und das ist ja wichtig für den folgenden Stoff..Hoffe wer kann helfen..

gruß

Hallo!
Mal eine Mathefrage von mir, es geht um meine Hausaufgaben (keine Angst ich will keine Lösung, habe nur nicht einmal den Ansatz einer Ahnung was ich tun soll).
Nun, unser Thema ist die Binomialverteilung. An sich schon schwer genug aber ich glaube grob verstehen tue ich die passenden Formeln. Jetzt haben wir aber eine Aufgabe bekommen, die mich völlig aus der Bahn wirft. Im Anhang ist ein Foto der Aufgabe inklusive meinen "Aufzeichnungen".
Es wäre echt toll wenn mir jemand erklären könnte, was ich zu tun habe...

Abbildung 1 zeigt einen Teil eines Baumdiagramms zu einem 4-stufigen Experiment mit einer Urne. In der Urne liegen 4 rote und 6 grüne Kugeln. Das Ziehen einer roten Kugel wird als Erfolg gewertet.

1. Ergänzen Sie das Baumdiagramm so weit wie möglich.
2. Berechnen Sie die Wahrscheinlichkeit dafür, dass bei einer Kette zunächst zweimal eine rote und dann zweimal eine grüne Kugel gezogen wird, also (r,r, g, g).

Ich komme bei dieser Aufgabe nicht weiter und würde mich sehr über Hilfe freuen, weil ich die Lösungsschritte gerne nachvollziehen wollen würde

2. Ein Unternehmen produziert Bauteile, von denen durchschnittlich 10% defekt sind. Ein Kunde kauft 30 Bauteile.

a) Berechnen Sie, wie viele defekte Bauteile bei einer Menge von 30 Bauteilen im Mittel zu erwarten sind.

b) Berechnen Sie die Standardabweichung von dem erwarteten Wert.

c) Berechnen Sie die Wahrscheinlichkeit für folgende Ergebnisse:

1. Es sind keine Bauteile defekt.
2. Es sind genau 5 Bauteile defekt.
3. Es sind höchstens 2 Bauteile defekt.
4. Es sind mindestens 3 Bauteile defekt.

Für a) würde ich die Formel E(X)= n* p nehmen = 30*10= 300 Defekte Bauteile

Ist hier p überhaupt 10?

b) Sigma(X)= Wurzel aus n*p* (1-p)

= Wurzel aus 30*10* (1-10)

Beim Ergebnis im Taschenrechner kommt mathematischer Fehler?

Bei c) komme ich nicht weiter und würde mich sehr über Hilfe freuen, wie ich das ausrechnen kann

Sind meine bisherigen Überlegungen und Ergebnisse richtig?

Hallo!

Die Wahrscheinlichkeitsaufgabe zu der ich eine Frage habe, lautet so:

In einer Urne befinden sich 10 gleichartige Kugeln, davon sind 8 schwarz und 2 weiß.Aus dieser Urne werden nun nacheinander 10 Kugeln gezogen, wobei nach jedem Zug die Kugel zurückgelegt wird.

Wie groß ist die Wahrscheinlichkeit genau 2 weiße Kugeln zu ziehen?

Ich weiß man muss die Bernoulli-Formel anwenden, aber wieso? Könnte man nicht einfach 10*(1/5²)*(4/5^8) rechnen?

Hallo Ihr Lieben, ich brauche bitte Hilfe bei dieser Rechnung. Es geht um Binomialverteilung🫣die Aufgaben B und C ganz unten auf dem Zettel finde ich am schwierigsten, also die kleinen Buchstaben …. Vielleicht könnt ihr mir Ansätze geben, wie ich das einfach lösen kann, da ich das bis morgen haben muss. Das wär sehr nett..

danke

Verzweifeln gerade an einer Mathe Aufgabe für das Studium bei der Klausurvorbereitung kann uns jemand aushelfen?

Es wird ein Würfel 4 mal nacheinander geworfen b.) Wie groß ist die Wahrscheinlichkeit eine Zahl kleiner als 14 zu würfeln unter der Bedingung dass der dritte Würfel eine 3 ist? 

Hallo,

ich habe mal nur eine inhaltliche Farbe. Wie sieht man, welche Würfel eine Rote Seiten haben? Denn ich sehe doch gar nicht alle Würfel und vor allem nicht von allen Seiten.

Moin Leute, ich habe eine Hausaufgabe welche ich leider nicht komplett verstehe. Muss ich quasi die relativen Wahrscheinlichkeiten für die 1,2,..6 herausfinden oder was ist genau verlangt. Wie gehe ich am besten vor ? Und dann soll ich die Ergebnisse erklären. Ich hoffe ihr könnt mir weiterhelfen

Ich habe eine Frage, unzwar wieso kann man bei (erstes Bild) J/s/A, das A in den Nenner packen, so dass J/A*s ergibt, aber (zweites Bild) bei cm³/cm³/s ist das nicht der Fall, stattdessen scheint s in den Zähler des Bruchs zu kommen da als Einheit s bleibt.

Die ersten 3 Aufgaben habe ich gelöst, bei E4 komme ich nicht weiter

Hallo, ich hätte eine Frage zu herleitung der Bonferroni-Ungleichung:

P(⋂k=1bis n ​Ak​)≥∑k=1 bis n ​P(Ak​)−(n−1)

Mein Lehrer hat begonnen, indem er :

P(⋂k=1bis n ​Ak​) = P(∪k=1 bis n​ Ak^c​)^c gesetzt hat, aber ist das nicht falsch?

Müsste nicht diese Gleichung stimmten:

P(⋂k=1bis n ​Ak​) = P(⋂k=1bis n ​Ak​^c)^c

weil P(A) = P(A^c)^c oder vertue ich mich?

Hallo! Ich bin mir ziemlich unsicher, ob das Experiment "Aus einer Serie von Glühlampen werden 5 ausgewält, die Brenndauer bestimmt und festgestellt, ob diese mindestens 1000 Stunden beträgt oder nicht." eine Bernoulli-Kette ist. Eigentlich ja, denn entweder beträgt die dauer mind. 1000 Stunden oder nicht, also gibt es 2 mögliche Ausgänge, oder? Mich verunsichert, dass nicht angegeben wurde, wie groß diese Serie überhaupt ist und dass so viele anderen Angaben dabei sind. Bin für jeden Tipp dankbar!

Hey ich kann mich leider nicht mehr genau dran erinnern, wie man diese Aufgabe rechnen. Vielleicht kann mir hier jemand helfen :

wäre super lieb ☺️

40% Musik , 30% Computerspiel, 20% fernsehen

Wie viele Jugendliche müssen mindestens befragt werden, um mit mindestens 99 % Wahrscheinlichkeit mindestens einen zu finden, der Computerspiele bevorzugt?

Hi, Ich hänge gerade an einer (Denke ich) Kniffligen Aufgabe, wäre echt cool wenn mir da jemand helfen könnte:

Der Speisesaal eines Restaurants hat 40 tische. Erfahrungsgemäß kommen 15% der Gäste die reserviert haben nicht. Deshalb nimmt der Besitzer mehr als 40 Reservierungen an.

a) welches Risiko geht der Besitzer ein, seine Gäste zu verärgern, wenn er 46 Reservierungen annimmt. b) wie viele Reservierungen sollte er nur annehmen, wenn das Risiko, einen Gast zu verärgern kleiner als 10% sein soll?

diese aufgebe soll mit dem GTR ausgerechnet werden Tabellenfunktion und die Grafische Ausgabe sind erlaubt. d.h. binomcdf/pdf

Gruß John (;

Hallo, ich lerne gerade, wie man den alpha und beta fehler berechnet bei einem Alternativtest.

z.B. haben wir n=20, 

Wenn man den Annahme bzw. Ablehnungsbereich von H_0 berechnen will, ergibt sich durch Ausprobieren des kritischen Werts "k", dass k=4 mit p_1=0,4 P=0,0509% ergibt, weil für k=5 schon P=0,1255 ist und die 10% Schwelle von p_0 übersteigen würde.

Wenn ich nun den Alpha fehler berechnen will, muss ich das ja über den Ablehnungsbereich machen. Das heißt, wir haben hier einen Ablehnungsbereich von [5;30] für H_0. Also rechnen wir P(x≥5) mit p_0=0,1 und erhalten 4,3%. Diesen Fehler möchten wir ja in Kauf nehmen aber den Beta Fehler unbedingt vermeiden.

Der beta fehler als Fehler 2. Art ergibt sich wenn wir das ja über den Annahmebereich berechnen also P(x ≤4) mit p_1=0,4 und erhalten 5,1%.

Aber was ist nun, wenn der Ablehnungsbereich von H_0 nicht rechts, sondern links ist? Weil der ist ja hier offensichtlich im rechten Bereich. Wie berechne ich dann Alpha/beta Fehler? Wie gesagt kann man den alpha Fehler ja berechnen, wenn man diesen über den Ablehnungsbereich berechnet. Gilt das dann hier für H_1, weil der Ablehnungsbereich von H_1 auf der rechten Seite ist? Also müssten wir P(x≥5) rechnen mit p_1=0,1

(wenn  )? Oder müssten wir in jeden Fall IMMER ÜBER DEN ABLEHNUNGSBEREICH VON H_0 den alpha fehler rechnen??

Hallo, bei folgender Aufgabe bin ich mir nicht sicher.

Entscheiden Sie, ob die folgenden Aussagen richtig sind und korrigieren Sie gegebenenfalls falsche Aussagen.

a) Wenn bei einer Bernoulli-Kette bei gleicher Treffer-Wahrscheinlichkeit p die Anzahl n der Versuche wächst, dann wachsen auch der Erwartungswert und die Standartabweichung.

b) Wenn bei einer Bernoulli-Kette bei gleicher Anzahl n der Versuche die Trefferwahrscheinlichkeit p wächst, dann wachsen auch der Erwartungswert und die Standartabweichung.

Danke im Voraus! :)

Ein im Jahr 07 zugelassener Pkw wird zufällig ausgewählt. () Geben Sie die Wahrscheinlichkeit der folgenden Ereignisse an: A: Der Pkw ist ein Elektroauto. B: Der Pkw wurde privat zugelassen und ist kein Elektroauto. (3) Bestimmen Sie die Wahrscheinlichkeit dafür, dass der Pkw ein Elektroauto ist, wenn er gewerblich zugelassen wurde. (6 + 3 + 3 Punkte) Im Folgenden werden die Verkaufszahlen eines großen Autohauses betrachtet, das sich auf den Verkauf von Elektrofahrzeugen spezialisiert hat. Im Vergleich zum Bundesdurchschnitt verkauft dieses Autohaus überdurchschnittlich viele Elektroautos. So ergab die Analyse der Vorjahresverkaufszahlen, dass 7,5 % der verkauften Autos Elektroautos waren. Diese empirisch ermittelte relative Häufigkeit soll im Folgenden als Wahrscheinlichkeit dafür angesehen werden, dass ein verkauftes Auto ein Elektroauto ist. Die Anzahl verkaufter Elektroautos wird im Folgenden als binomialverteilt angenommen. b) () Das Autohaus stellt eine Prognose für die nächsten 000 Autoverkäufe auf. Bestimmen Sie die Wahrscheinlichkeit folgender Ereignisse: E : Es werden genau 80 Elektroautos verkauft. E : Es werden mindestens 70, aber höchstens 80 Elektroautos verkauft. E 3 : Die Anzahl der verkauften Elektroautos entspricht genau dem Erwartungswert. () Ermitteln Sie, wie viele Autos mindestens verkauft werden müssen, damit darunter mit einer Wahrscheinlichkeit von mindestens 90 % mindestens ein Elektroauto ist. 

Ich brauche Hilfe bei einer Mathematiksufgabe

"Eine gezinkte Münze wird 120 mal geworfen. Die Wahrscheinlichkeit für das Ergebnis Zahl beträgt P(Z) =0,45.

Wie oft wird das Ergebnis Wappen erwartet?"

Wie kommt man auf 0,45 und wie berechnet man das Ergebnis für Wappen?

Einen wunderschönen guten Abend,

wo ist hier mein Denkfehler bei den Aufgaben e) und f)? Denn die Ergebnisse weichen von den der Lösung stark ab. Möglicherweise ist mein Rechenweg bei d) auch falsch und nur durch Zufall richtig. Es kann natürlich auch sein, dass die Lösung (teilweise) falsch ist.

Aufgabe:

Lösung:

Hilfreiche Informationen für euch, um diese Aufgabenstellung zu verstehen, falls ihr es so noch nicht kanntet. Denn es gibt ja die Unterschiede zwischen B(n;p(k)) und F(n;p(k)):

Also ich raff es einfach nicht. Bei einem Bernoulli Versuch habe ich ja immer zwei Ergebnisse entweder das gewünschte Ereignis tritt ein oder eben nicht. Und bei bernoulli versuchen habe ich ja eine gewisse Wahrscheinlichkeit p schon gegeben. Das sowie k für die anzahl der treffer und n für die Anzahl der versuche kann ich einfach in die Formel eingeben und bekomme dann doch die Wahrscheinlichkeit für das Eintreten des gewünschten Ereignis oder nicht?

Und was hat das jetzt mit der Binomialverteilung zu tun?? Im Internet steht das die Biniomalverteilung alle möglichen Resultate eines Bernoulli-Experimentes/Kette ist...aber ich habe doch nur das Resulatat, mit welcher Wahrscheinlichkeit ein Ereignis eintritt. Wie funktioniert die Binoialverteilung und was genau macht sie??

Bitte helft mir

Hallo, kennt sich jemand im R Studio aus und könnte mir bei der Binomialverteilung helfen?

12 % Plagiate

300 Abschlussarbeiten

Zufallsvariable X

wie löse ich das im R?

Danke

Ein Glücksrad trägt auf seinen zehn gleich großen Feldern die Ziffern 0 bis 9. Es wird sechsmal gedreht.

Mit welcher Wahrscheinlichkeit sind die ersten vier Ziffern gerade .

Also das Ereignis ist (gggguu) und (gggggg) und somit 1/32 .Ich weiß leider nicht ,ob ich es richtig gelöst habe. Kann mir es bitte jemanden erklären

Was muss ich für B in den Taschenrechner eingeben?

Ich möchte nicht die Lösung der Aufgabe, sondern nir wissen, welche Werte in den Taschenrechner sollen, damit ich es mir erklären kann 🤗