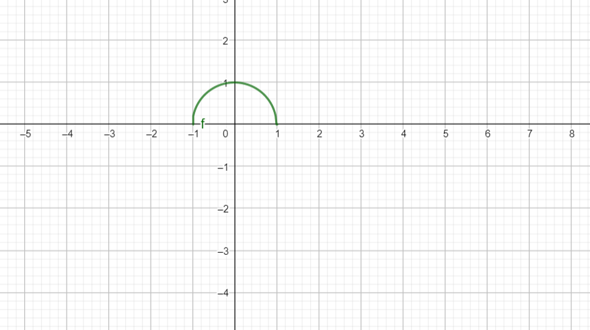
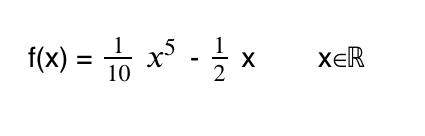Was kann man tun, wenn man durch alle Klausuren gefallen ist?
Hi zusammen,
wie es der Titel schon sagt, bin ich durch alle Klausuren (3 sind es an der Zahl) gefallen. Ich studiere Gymnasiallehramt mit den Fächern Mathe und Philosophie im ersten Semester.
Ich bin absolut gar nicht mit dem Onlineangebot klar gekommen, ich hing immer sehr viele Vorlesungen hinterher, da ich immer mit den Aufgaben (Matheblätter, Philosophie und BW- Essays) beschäftigt war. Die Aufgaben habe ich immer beim 1.Versuch bestanden, weil ich da viel Zeit reingesteckt habe. Grundsätzlich hatte ich einfach einen sehr schlechten Start ins Unileben. Durch das Onlinesemester war ich noch nie an der Uni, kenne keine Kommilitonen oder konnte auch sonst kein Angebot aus der Uni nutzen, musste mich also ganz alleine irgendwie durchboxen. Ich bin auch die erste in der Familie die studiert.
Ich war quasi das ganze Semester lang nur allein in meinem Zimmer. Das hat auch ganz schön an der Motivation gezerrt.
Lange Rede kurzer Sinn: ich habe die Klausuren in Mathematik und Philosophie nicht bestanden und weiß jetzt gar nicht was ich machen soll. Soll ich im nächsten Semester einfach genau die gleichen Module nochmal belegen und alles nochmal machen? Oder soll ich weiter nach der Studienordnung gehen und die Wiederholungsklausuren dann noch dazu schreiben? Oder einfach ganz mit den Studium aufhören? Ich weiß es nicht. :(
Vielleicht könnte ja jemand seine Erfahrungen mit mir teilen, ich wäre sehr dankbar.
LG
HSLT