Wie kommt man hier weiter?
Hallo ich komme bei einer Aufgabe gar nicht weiter. Es wäre sehr nett wenn mir da jmd helfen kann
1 Antwort
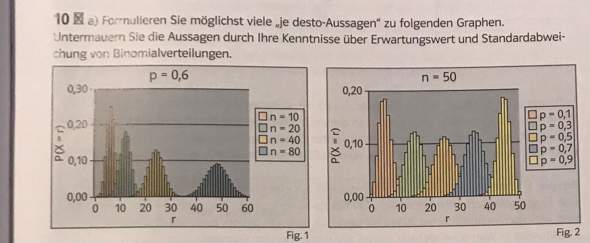
Zur linken Grafik:
Je höher bei konstanter Wahrscheinlichkeit für Erfolg der Stichprobenumfang ist, umso gleichmäßiger, breiter und genauer wird die Wahrscheinlichkeitsverteilung,, sinkt die Wahrscheinlichkeit des Mittelwertes (Erwartungswert) und vergrößert sich die Standardabweichung.
Zur rechten Grafik
Ändert sich bei konstantem Stichprobenumfang die Wahrscheinlichkeit für Erfolg, so zeigt sich zu p=0,5 nach rechts UND links ein gleichmäßig verschobenes Histogramm, mit jeweils zunehmender Wahrscheinlichkeit für den Erwartungswert und damit verbundener Abnahme der Standardabweichung.
Was anderes fällt mir dazu nicht ein, außer, dass man hier das Gesetz der großen Zahlen näher erläutern will:
Das Gesetz der großen Zahlen ist ein Grenzwertsatz aus der Wahrscheinlichkeitslehre mit großer praktischer Bedeutung. Es beschreibt im einfachsten Fall, dass sich die relative Häufigkeit h_n(A) eines Zufallsereignisses A an die theoretische Wahrscheinlichkeit P(A) dieses Ereignisses annähert, wenn das Zufallsexperiment nur oft genug durchgeführt wird. In anderen Worten geht die Differenz zwischen der beobachteten relativen Häufigkeit und der theoretischen Wahrscheinlichkeit eines Ereignisses für unendlich viele Durchgänge des Zufallsexperiments gegen null. Für eine sehr große Anzahl an Wiederholungen weicht also die beobachtete relative Häufigkeit nicht mehr bedeutend von der wahren Wahrscheinlichkeit eines Ereignisses ab.
In der Praxis bedeutet das Gesetz der großen Zahlen, dass wir den Erwartungswert von Zufallsvariablen gut mit dem Stichprobenmittelwert schätzen können. Dabei gilt: Je größer der Stichprobenumfang, desto besser schätzen wir den Erwartungswert.