Wie rechnet man diese Aufgabe (Stochastik)?
Im vergangenen Monat wurden beim Straßenverkehrsamt einer Stadt 5239 Fahrzeuge angemeldet, darunter 1774 eines bestimmten Herstellers. In den ersten 2 Tagen dieses Monats wurden 449 Fahrzeuge angemeldet. Bei welcher Zahl von Fahrzeugen des betreffenden Herstellers würde man sagen, dass sich der Anteil der Neuzulassungen geändert hat? (a =5%)
Danke im Voraus
2 Antworten
die Wahrscheinlichkeit kann mit p=1774/5239 berechnet werden
da es sich nur um den Anteil des einen Herstellers an der Gesamtzahl handelt, spielen die 2 Tage keine Rolle
man führt einen zweiseitigen Hypothesentest durch mit n=449 und der berechneten Wahrscheinlichkeit. Es wird der untere und der obere Ablehnungsbereich ermittelt. Liegt die Zahl in einem der Ablehnungsbereichen, dann hat sich der Anteil verändert
ich gehe davon aus, dass der zweiseitige Hypothesentest kein Problem darstellt. Das Signifikanzniveau von 5% wird auf 2,5% jeweils im unteren und im oberen Bereich aufgeteilt
P(X<=k)<=0,025
n=449, p=0,339
binomialcdf
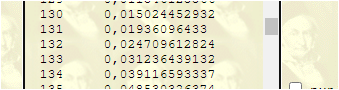
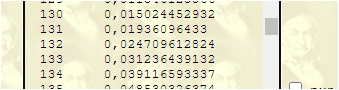
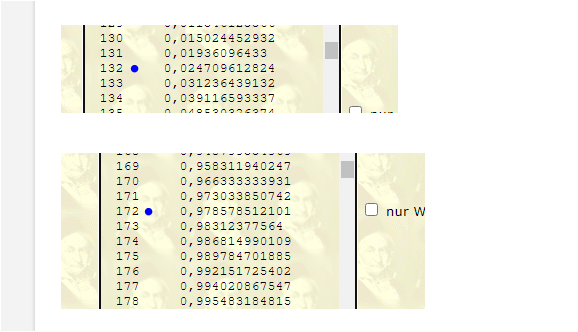
k=132: 0,024
k=133: 0,030
der untere Ablehnungsbereich ist [0;132]
P(x>=k)<=0,025
1-P(x<=k-1)<=0,0025
P(x<=k-1)>=0,975
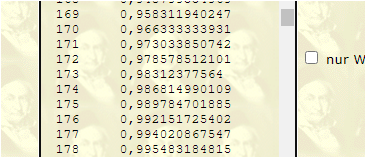
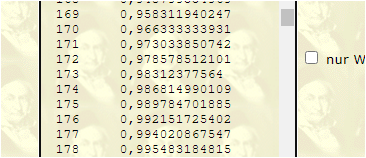
k-1=171: 0,972
k-1=172: 0,978 => k=173
oberer Ablehnungsbereich [173;449]
liegt der Wert zwischen 133 und 172, dann hat sich der Anteil nicht verändert (bei einem Signifikanzniveau von 5%)
ich bin vom Kenntnisstand eines baden-württembergischen Abiturienten ausgegangen. Bis zum Abi werden da nur die einseitigen und zweiseitigen Hypothesentests bei der Binomialverteilung behandelt. Es kann durchaus sein, dass man solche Aufgaben auch anders lösen kann. Der erwähnte Test nach Fischer sagt mir beispielsweise nichts
ich denke auch ,dass man im Abi "rustikal" mit solchen empirischen W umgeht.
k = 171 ........0.9730
k = 172 ........0.9785
.würde nicht k = 172 schon ausreichen , schließlich , denn 0.9750 ist doch schon überschritten ???
rechts verschiebt sich immer die Grenze wegen
P(X>=k) = 1 - P(X<=k-1)
mit binomcdf kann man nur P(X<=k) ausrechnen und nicht P(X>=k)
man liest also den k-1 Wert ab
172 stimmt schon, aber das ist dann k-1
Ich habe da jetzt für k 169 raus, aber was heißt das jetzt genau?
und warum n=449 und nicht 1774
die 1774 braucht man für p .
und p ist die W dafür , dass ein neuzugelassener Wagen von der Firma ist . Und dieses Zufallsexperiment wird eben n = 449 wiederholt.
p = 1774/5239
.
H0 P = p
H1 P ungleich p
.
Bino-Verteilung mit p und n = 449
Bei alpha = 0.95 und zweiseitig
sieht man , dass bei ? 0.025 unten und bei ? 0.025 oben abgeschnitten werden.
so weit so fertig
.
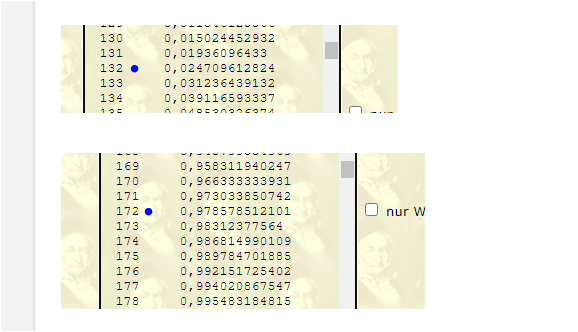
132 oder weniger und 172 oder mehr !!! ( natürlich nicht weniger )
Was haben Sie jetzt genau gerechnet? Und was heißt jetzt k=169 für den Annahmebereich
Ich war doch noch nicht fertig , habe ich doch geschrieben !!!
k = 169 ist der k-Wert für einen einseitigen . Es heißt aber "verändert" , dh weniger oder mehr als "normal" muss geprüft werden.
Verstehe ich jetzt nicht ganz ehrlich gesagt
Das habe ich mir auch schon überlegt, aber tatsächlich ist das auch nur eine Schätzung. Die Problemstellung erinnert mich eher an einen Exakten Test nach Fischer, was ich aber für unwahrscheinlich halte, dass es in der Schule gefragt wird.