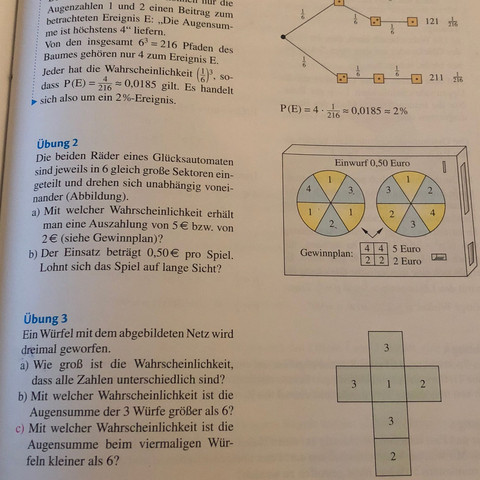
Wie oft muss ich eine Münze werfen, bis ein mal eine Serie von X mal Kopf zu erwarten ist?
Kurzum, es geht um das nacheinanderwerfen einer Münze, und es soll so lange geworfen werden, bis man X mal (hier Beispiel: 5) hintereinander Kopf geworfen hat. Dabei ist der Wurf nicht aufzuteilen, sondern es soll einfach hintereinanderweg geworfen werden, also nicht 5 mal werfen, schauen ob alles Kopf war, wenn nicht nochmal 5 mal werfen usw...
Die Chance auf 5 x Kopf ist (1/2)^5 = 1/32, dennoch sollte keiner der beiden "naiven" Ansätz stimmen:
1) Jeder 5er-Block einzeln betrachtet, also ist das Ergebnis dass nach 32 5er-Blöcken mal eine 5er-Serien zu erwarten ist. Das ist falsch, schließlich können ja auch die letzten beiden würfe des Xten Wurf-Blocks und die ersten 3 Würfe des X+1ten Wurf-Blocks Kopf sein...
2) Würfe 1,2,3,4,5 sind ein Block, Würfe 2,3,4,5,6 sind ein Block, Würfe 3,4,5,6,7 sind ein Block etc sollte auch nicht stimmen, schließlich sind die Blöcke nicht voneinander unabhängig. Wenn 1,2,3,4,5 alles Zahl ist, dann kann 2,3,4,5,6 ja nicht alles Kopf sein und hat per se keine Chance...
Daher nun meine Frage einfach um meine Neugier zu befriedigen: Wie geht man so ein Problem an?