Hilfe zu Stochastik in Mathe - Ich wäre euch sehr dankbar?
Hallo, ich schreibe übermorgen eine Klausur in Mathe zu Stochastik. Diese Übungsklausur habe ich bearbeitet und ich wäre sehr dankbar, wenn jemand meine Lösungen kontrollieren könnte. Über Verbesserungsvorschläge würde ich mich sehr freuen! Bei Aufgabe 5,6,8 und 9a weiss ich leider den Ansatz nicht. Könnte mir da einer helfen? Bei 7a und b sowie bei 9a bin ich mir sehr unsicher über meine Lösung. Über eine Kontrolle und Hilfe wäre ich sehr dankbar!
Anbei die Aufgaben und meine Bearbeitung.
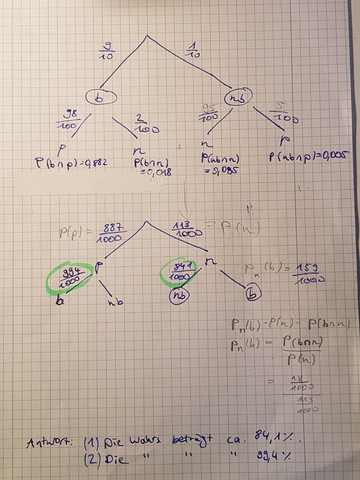
2 Antworten
Hallo,
bei Aufgabe fehlt Dir der Ansatz.
Wenn 10 Angestellte eine Schreibkraft für je 12 Minuten in der Stunde benötigen, sind das 10*12=120 Arbeitsminuten für Schreibkräfte (durchschnittlich).
Da eine Stunde aber nur 60 Minuten hat, braucht man für 120 Minuten auf jeden Fall zwei Kräfte, die dann im Schnitt voll ausgelastet wären.
Es sind aber drei Schreibkräfte vorhanden. Das bedeutet, daß sie zu 2/3 ausgelastet sind und zu 1/3 frei sind.
Die Wahrscheinlichkeit dafür, daß eine Schreibkraft frei ist, beträgt demnach 1/3.
Die Wahrscheinlichkeit dafür, daß von drei Schreibkräften genau eine zur Verfügung steht, beträgt daher (3 über 1)*1/3*(2/3)²=0,444=44,4 %.
Hier geht es aber wohl mehr darum, daß überhaupt eine Kraft zur Verfügung steht, es dürfen also auch 2 oder 3 sein.
Entweder berechnest Du auch noch die Wahrscheinlichkeiten für k=2 und k=3 nach der bekannten Formel (n über k)*p^k*(1-p)^(n-k) oder Du berechnest die Wahrscheinlichkeit dafür, daß alle drei beschäftigt sind und ziehst die von 1 ab:
Die Wahrscheinlichkeit dafür, daß eine Kraft beschäftigt ist, liegt bei 2/3, daher:
(3 über 3)*(2/3)^3*(1/3)^0=(2/3)^3=8/27.
Damit liegt die Wahrscheinlichkeit für eine bis drei freie Kräfte bei 1-8/27=19/27.
In Teil b) soll berechnet werden, wie viele Schreibkräfte es braucht, damit immer zu 95 % Wahrscheinlichkeit eine frei ist.
Auch hier gehst Du über das Gegenereignis: Keine ist frei. Die Wahrscheinlichkeit hierfür muß auf unter 5 % oder 0,05 sinken.
Die Wahrscheinlichkeit für Beschäftigung liegt bei 2/k (Arbeit für zwei Kräfte geteilt durch die vorhandenen Kräfte).
Du rechnest also (k über k), was 1 ergibt, mal (2/k)^k*(1-2/k)^0, also auch hier eine 1, so daß die Ungleichung (2/k)^k<0,05 bleibt, was am besten durch Probieren erledigt wird.
Kleiner Tipp: Viel mehr als drei müssen es nicht sein und für k setzt Du nur ganze Zahlen ein. Du mußt nicht auf genau 0,05 kommen, sondern auf den ersten Wert, der unter 0,05 liegt.
Herzliche Grüße,
Willy
Bei 7a gehst Du über die Binomialdichte mit n=3, k=2 und p=0,05
Wahrscheinlichkeit für 2 fehlerhafte von 3 Geräten also (3 über 2)*0,05^2*0,95^1
7 b geht entsprechend mit k=0 bis k=3, n=10 und p=0,05
Summe der Einzelwahrscheinlichkeiten bilden.
Wenn Du die Funktion der kumulierten Binomialverteilung auf dem Rechner hast, gibst Du n=10, k=3 und p=0,05 ein. Er summiert dann automatisch von k=0 bis k=3.
Für die 6 habe ich im Moment keine Zeit.
vielen Dank! Hast mir sehr geholfen! :) Wenn du bis morgen früh noch Zeit findest, könntest du mir zu der anderen Aufgabe auch den Ansatz geben und schauen ob die Aufgabe 2,3 und 4 richtig gemacht worden sind von mir? Liebe Grüße
Bei Aufgabe 6 könntest Du überlegen, daß ein Gerät die Chance von (399/400)^60 hat, keinen Pixelfehler aufzuweisen.
Die Pixelfehler sitzen alle um eine Urne herum mit 400 numerierten Kugeln, ziehen eine Kugel, notieren sich die Nummer des Gerätes, die sie gezogen haben und legen die Kugel zurück.
Für die Geräte besteht also bei jedem Zug eine Chance von 399/400, daß sie nicht gezogen werden, also keinen Fehler abbekommen.
Das Ganze hoch 60 ergibt die Chance, ganz ohne Fehler durchzukommen.
Die Aufgabe ist wieder relevant... und sehr wichtig.. Zu der von dir erläuterten b) hätte ich noch ne frage.. Ein Mathecoach meinte dein Ansatz zu der b) wäre falsch weil man das so in der Ungleichung nicht aufschreiben könne... Er meinte: (2/3)^k muss grösser gleich 0,5 sein (Ich denke wenn dann kleiner gleich). Aber bei seinem Ansatz kommt 8 raus und bei deinem 5... Jetzt bin ich sehr verwirrt... Und was hast du bei q (1-2/k) als hochzahl eingesetzt? k-k, sodass da 0 rauskommt? Dies hoch null kommt dann aber ja 0 raus nicht 1.
Danke im Voraus!
Kein Personalchef würde acht Schreibkräfte einsetzen, pro Stunde 120 Arbeitsminuten anfallen.
Eine allein könnte es nicht schaffen. Zwei wären bei perfekter Absprache der Angestellten permanent beschäftigt, so daß noch eine oder eine halbe Kraft eingestellt würde und basta.
Soweit die Realität.
Mathematisch würde ich es nun lieber über die Poisson-Verteilung berechnen, die nur vom Erwartungswert abhängt.
Der Erwartungswert ist, da pro Stunde 120 Arbeitsminuten anfallen und eine Schreibkraft 60 Minuten bewältigen kann, daß zwei Kräfte beschäftigt sind.
Die Wahrscheinlichkeit, daß k Kräfte beschäftigt sind, berechnet sich dann nach der Formel P(k)=(µ^k/k!)*e^(-µ)
Wenn Du also die Wahrscheinlichkeit dafür berechnen möchtest, daß eine von 3 Kräften gerade frei ist, würdest Du die Wahrscheinlichkeiten von k=0 bis k=2 addieren. Das wäre bei µ=2 und k=0;1;2:
(2^0/0!+2^1/1!+2^2/2!)*e^(-2)=0,6767
Entsprechend läge die Wahrscheinlichkeit bei 5 Schreibkräften bei
(2^0/0!+...+2^4/4!)*e^(-2)=0,9473, also knapp unter 95 %, so daß nach dieser Berechnung eine sechste Kraft eingestellt werden müßte.
Allerdings ist die Poisson-Verteilung nur eine Näherung und bei sechs Kräften wäre bereits eine Wahrscheinlichkeit von deutlich über 98 % erreicht, daß wenigstens eine von ihnen gerade frei ist, so daß die Zahl 5 durchaus realistisch ist. Allerdings wäre auch diese aus finanzieller Sicht eher unvernünftig zu nennen, es sei denn, die Schreibkräfte bekämen noch Zusatzaufgaben in den freien Zeiten, die bei Bedarf unterbrochen werden können.
Ansatz über die Binomialverteilung:
Wahrscheinlichkeit dafür, daß ein Angestellter eine Schreibkraft benötigt: p=0,2 (12 Minuten sind 20 % von einer Stunde).
Wenn m Schreibkräfte vorhanden sind, ist mindestens eine frei,
wenn höchstens k=m-1 Schreibkraft beschäftigt sind.
Du siehst also in der Tabelle der kumulierten Binomialverteilung nach, für welchen Wert für k bei n=10 und p=0,2 der Wert auf über 0,95 ansteigt.
Das ist bei k=4 (0,9672) der Fall.
Wenn bis zu vier Schreibkräfte beschäftigt sind, brauchst Du eine fünfte, die dann noch frei ist.
Vielen Dank! Ist also 4 richtig, oder 5? Weil bei 4 übersteigt es ja die 95%... Sonst könnte ja man argumentieren, dass bei 3 sie beschäftigt sind, und bei 4 einer mind. frei ist, oder nicht?
Und wäre dein Ansatz am Anfang mit (2/k)^k<0,05 auch richtig?
Undd bei der Aufgabe 6 blicke ich jetzt bei a) und c) endlich mehr durch. Könntest du schauen ob die soweit richtig ist? Die b) verstehe ich leider noch nicht.. Könntest du mir da bitte eine Lösung geben?
a)
P(X = 0) = COMB(60, 0)·(1/400)0·(1 - 1/400)^(60 - 0) = 0.8605
400·0.8605 = 344.2 → Wir erwarten ca. 344 Geräte ohne Pixelfehler
P(X = 1) = COMB(60, 1)·(1/400)1·(1 - 1/400)^(60 - 1) = 0.1294
400·0.1294 = 51.76 Wir erwarten ca. 52 Geräte mit einem Pixelfehler
c) 400·p = 380 → p = 0.95
P(X = 0) = COMB(n, 0)·(1/400)0·(1 - 1/400)^(n - 0) = 0.95 → n = 20,49166
Muss man jetzt abrunden oder aufrunden?
Danke im Voraus und LG!
Die 5 ist richtig. Dann sind bis zu vier Kräften bis zu 95 % beschäftigt, so daß die 5. noch frei ist.
Zu dem Ansatz mit (2/k)^k <0,05 : Wieso bleibt es so als gesamtes übrig? Wieso (2/k)^k übrig bleibt, habe ich verstanden aber nicht im Zusammenhang mit <0,05. Wie sah die Gesamte Gleichung denn mit eem Teil "<0,05>" aus? (Es geht mir grad nur um die Schreibweise, wie ich das dann aufschreibe). Danke im Voraus! lG
Aufgabe 5. )
https://www.mathelounge.de/84624/mit-welcher-wahrscheinlichkeit-es-in-der-kantine-personen
Musst du an deine Zahlenwerte anpassen, denn die Erschaffer deines Buch waren immerhin clever genug, die Zahlenwerte zu ändern.
Mit COMB ist auf der Webseite ein Binominalkoeffizient gemeint.
Diese Webseite hilft auch :
eine Frage: was ist mein n bei 4 b und c?(siehe seite auf mathelounge) weil in der formel steht nur hoch n...
ja meinte bei aufgb 5 die du mir verlinkt hast. da heisst die aufgbabe 4
also bleibt das n immer bei allen aufgabenteilen konstant?
und geht das irgendwie mit n über k? weil comb hatten wir noch nicht
Stimmt, das habe ich auch schon auf Taschenrechnern gesehen.
vielen Dank! Könntest du mir eventuell auch bei der 6 und 7 helfen? Wäre sehr nett!