Bitte keinen klugen Ratschläge oder dumme Sprüche - ich würde gern die mir bekannte Lösung verstehen bzw. wie man dahin gekommen ist! DANKE!!!!!
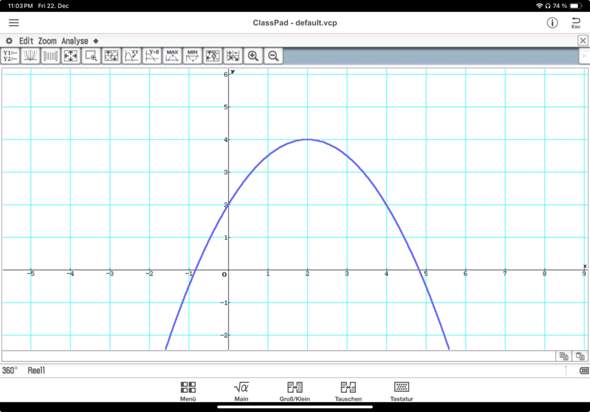
Aufgabe Mathe: Jan fährt gleichmässig mit einer Geschwindigkeit von 25 km/h. 20 Minuten später nach ihm startet Piet vom gleichen Startpunkt aus auf der gleichen Strecke mit einer Durchschnittsgeschwindigkeit von 45km/h
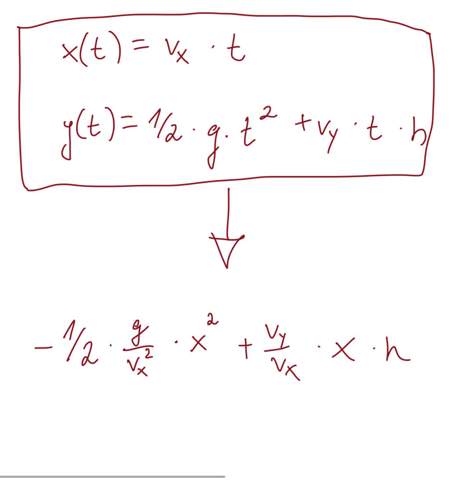
a) Stelle die Funktionsgleichung auf, wobei der Zeit (in h) die zurückgelegte Strecke (in KM) zugeordnet wird
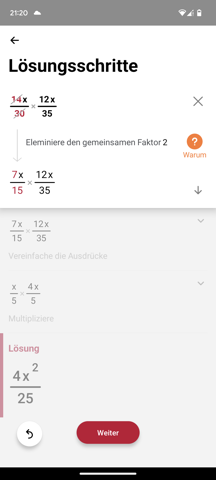
Lösung: Jan = J(t) = 25t / Piet = p(t) = 45t - 15
b) Wann hat Piet dann Jan eingeholt?
Piet hat Jan nach 25 Minuten eingeholt
Lösungsweg: J(t) = P(t) - somit
25t = 45t - 15 und t 0,75
0,75h = 45 min und 45 Minuten - 20 (Minuten des späteren Start) = 25 Minuten
Kann mir jemand helfen und erläutern, wie die Lösungen zustande kommen (z.B. bei a: 25t versteh ich ja noch und 45t auch, aber woher resultieren hier die -15?
b) 25t = 45t -15 resultiert dann ja wohl aus a, aber woher kommen die t =0,75
Vielleicht einfach zu viel gelesen / geübt mit meiner Tochter - aber hier hab ich leider völlig ein Brett vorm Kopf und versteh es nicht mehr.....
Vielen lieben Dank.
VG
Marco