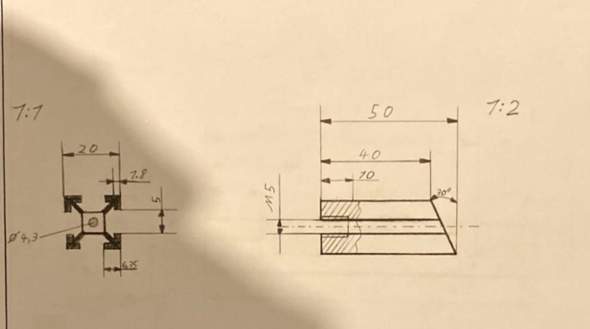
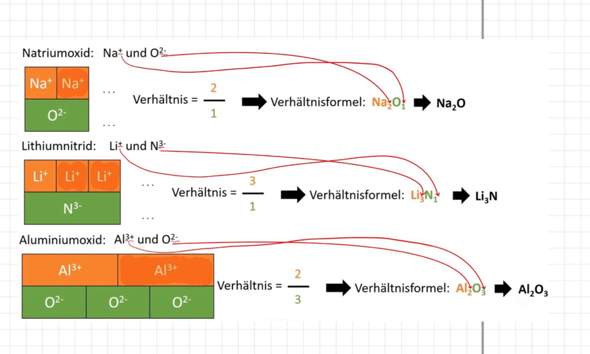
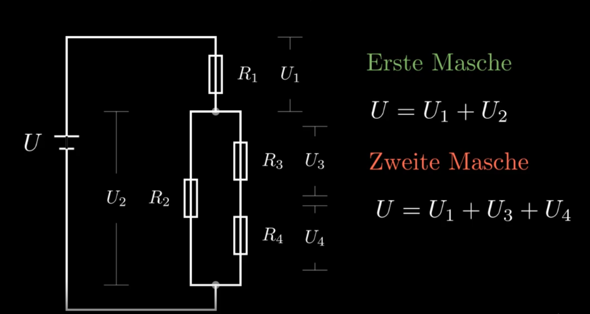
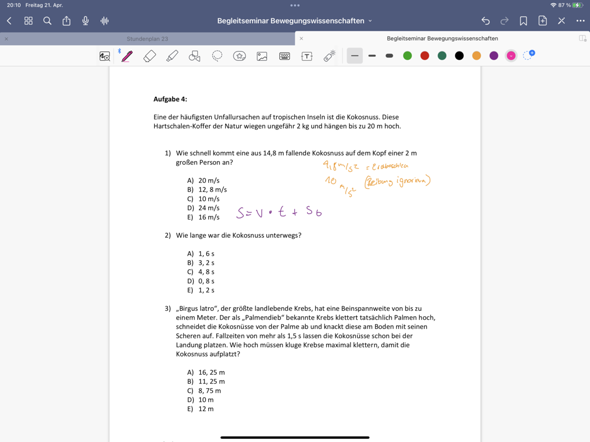
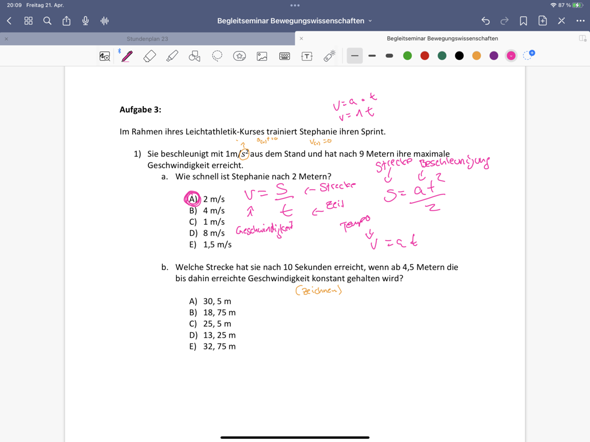
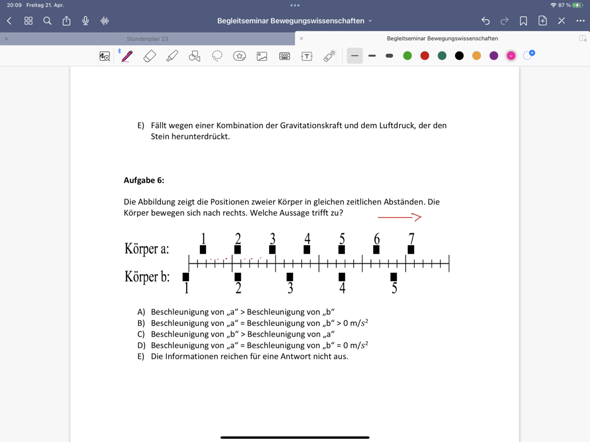
Hi. Ich habe mich mal spaßeshalber an eine Physikaufgabe gesetzt und bin mir nicht ganz sicher, ob ich diese richtig gerechnet habe.
Hier einmal die Aufgabenstellung:
Bei einer wissenschaftlichen Untersuchung beschleunigte ein Wanderfalke, der auf einer Höhe von 372 m flog, von 40km/h, um nach 16 Sekunden eine Taube auf einer Höhe von 38m über dem Erdboden zu schlagen. Die horizontale Distanz zwischen den Messpunkten betrug dabei 702m.
a) Berechne die mittlere Beschleunigung des Wanderfalken während seines Sturzfluges.
Hier einmal meine Rechnung:
Ich habe zur Überprüfung auch noch einmal ChatGPT gefragt.
Die Lösung von ChatGPT und mir stimmen nicht überein.
Hier der Lösungsansatz von ChatGPT:
Zunächst müssen wir die Endgeschwindigkeit des Wanderfalken berechnen, wenn er die Taube schlägt. Wir können die kinematische Gleichung verwenden:
v_f^2 = v_i^2 + 2ad
wobei v_f die Endgeschwindigkeit ist, v_i die Anfangsgeschwindigkeit, a die mittlere Beschleunigung und d die Entfernung zwischen den Messpunkten.
Da der Wanderfalke von 40 km/h auf Null beschleunigt, ist seine Anfangsgeschwindigkeit v_i = 40 km/h = 11.11 m/s. Die Entfernung zwischen den Messpunkten ist d = 702 m. Wir setzen diese Werte in die Gleichung ein und lösen nach v_f auf:
v_f^2 = (11.11 m/s)^2 + 2a(702 m)
v_f^2 = 123.21 m^2/s^2 + 1404a
v_f^2 - 1404a = 123.21 m^2/s^2
v_f^2 = 123.21 m^2/s^2 + 1404a
v_f = sqrt(123.21 m^2/s^2 + 1404a)
Als nächstes müssen wir die Zeit berechnen, die der Wanderfalke benötigt hat, um von einer Höhe von 372 m auf eine Höhe von 38 m zu fallen. Wir können die kinematische Gleichung verwenden:
d = v_it + 0.5a*t^2
wobei d die Höhendifferenz, v_i die Anfangsgeschwindigkeit, a die mittlere Beschleunigung und t die Zeit ist. Da die Anfangsgeschwindigkeit des Wanderfalken Null ist, vereinfacht sich die Gleichung zu:
d = 0.5at^2
Wir setzen die Werte ein und lösen nach t auf:
334 m = 0.5a(16 s)^2 334 m = 128a a = 2.61 m/s^2
Schließlich können wir die mittlere Beschleunigung des Wanderfalken während des Sturzfluges berechnen, indem wir v_f und v_i sowie die Zeit, die der Wanderfalke benötigt hat, um von 372 m auf 38 m zu fallen, kennen:
a = (v_f - v_i) / t
a = (sqrt(123.21 m^2/s^2 + 1404a) - 11.11 m/s) / 16 s
a = (sqrt(123.21 m^2/s^2 + 1404*2.61 m/s^2) - 11.11 m/s) / 16 s
a = 9.81 m/s^2
Die mittlere Beschleunigung des Wanderfalken während seines Sturzfluges beträgt 9.81 m/s^2, was der Beschleunigung aufgrund der Schwerkraft entspricht.