Guten Tag liebe Community,
ich habe ein kleines Problem mit OpenOffice Calc.
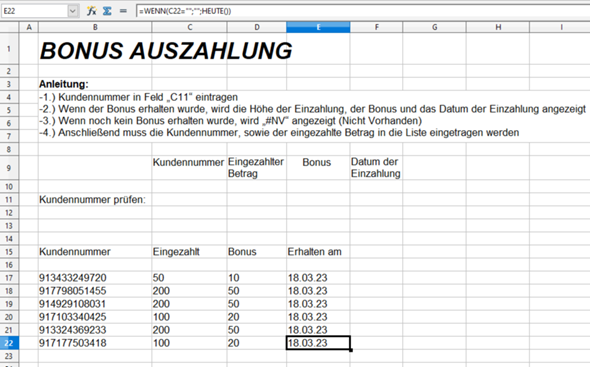
Ich habe eine Liste erstellt, in welcher ich Kundenkartennummern eintragen kann und die höhe des eingezahlten Geldes.
Der Bonus wird automatisch ermittelt.
Des weiteren möchte ich, dass das Datum automatisch eingetragen wird, sobald ich eine neue Kundenkartennummer hinzufüge.
Mein Problem ist, dass das Datum jeden Tag angepasst wird.
D.H. wenn ich die Datei am nächsten Tag öffne, aktualisiert das Programm automatisch bei jeder neuen Eintragung das Datum, sodass in der Spalte "Datum" immer das aktuelle Datum steht.
(Dies passiert auch, wenn ich zum Test das Datum des Rechners einen Tag weiter stelle und eine weitere Kundenkartennummer hinzufüge)
Gibt es eine Möglichkeit, dass das Datum automatisch ausgefüllt wird, (an dem Tag wo ich die neue Kundenkarte hinzufüge), OHNE das sich das Datum am nächsten Tag automatisch anpasst?
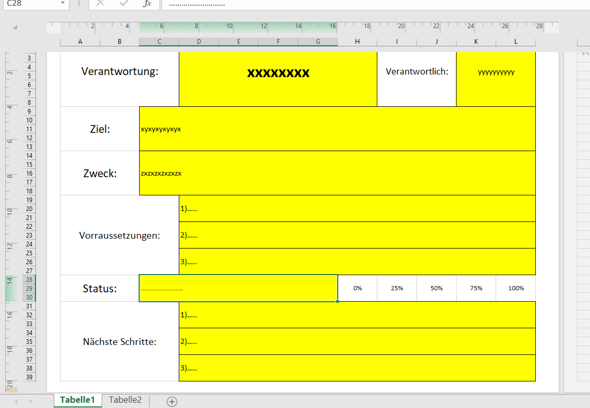
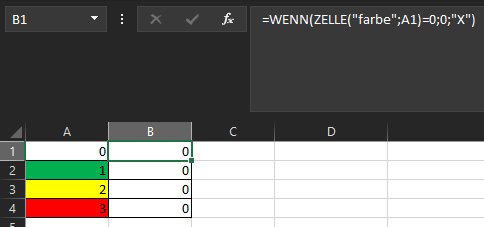
Anbei mal ein Beispiel Bild. Überall wird der 18.03.23 angezeigt, obwohl ich die erste Kundennummer schon am 16.3.23 hinzugefügt habe.
Wenn ich morgen eine weitere Nummer hinzufüge, wird überall der 19.3.23 eingetragen und das ist ja nicht Sinn und Zweck der Sache.
(und noch eine Kleinigkeit, wenn ich die spalten C und D formatiere zu "Währung", werden mir die zahlen Trotzdem normal angezeigt, ohne Nachkommastellen und dem € Zeichen. In den Einstellungen habe ich aber extra drauf geachtet, dass die Kommastellen und das Währungszeichen angezeigt werden sollen.
Wo liegt da der Fehler?)
Vielen Dank im voraus!