Integral elektrischer Fluss?
In den vorherigen Folien wurde der el. Fluss mit einer einfachen, komplizierten, und Kugelfläche mit einer Punktladung drin erklärt.
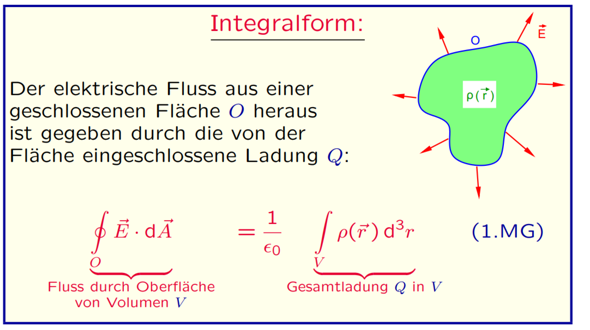
Aber was ist mit dieser Folie? Ich habe gelesen, dass der Kreis im Integral geschlossenes Integral heißt. Aber was bedeutet so etwas? Und was soll das in der Folie überhaupt bedeuten, was wird da berechnet?
Ist die geschlossene Fläche sowas wie eine Kugel mit einer eingeschlossenen Ladung?
Und die erste Formel ist doch ein normaler elektrischer Fluss oder? Oder bedeutet das wegen dem Kreis im Integral was anderes?
Ist rho da die Ladungsdichte? Heißt das dann, bei dem Volumenintegral wird die Masse berechnet wegen rho*V?
Wieso steht da 1/Epsilon0 davor? Das kenne ich von den allgemeinen E(r) Formeln, aber wo ist dan der Rest der Formel? Und wenn mit dem Volumenintegral tatsäclich die Masse berechnet wird, von was soll das dann die Masse sein?
3 Antworten
Bei einer eine Ladung umschließenden Fläche ist die "Anzahl" der durch die Fläche hindurchgehenden Feldlinien unabhängig von der Art der Fläche. Als Maß für die Feldlinienzahl kann man die elektrische Feldstärke sehen. Bei einer Kugelfläche, mit der Ladung im Zentrum, ist die Feldstärke überall gleich. Als Maß für die Anzahl der Feldlinien kann also der Term E(r)* 4 * pi * r^2 gelten. Dieser ist proportional zur Ladung. Also Q = k * E(r) * 4 * pi * r^2 oder E(r) = 1/k * Q / (4 * pi * r^2).
Bei Flächen, die keine Kugelflächen sind, geht die Summation der Feldlinien in die Berechnung des Integrals über. Enthält ein Volumen keine Ladung, so muß die Anzahl der "eintretenden" Feldlinien und die Anzahl der "austretenden" Feldlinien gleich sein. Das Integral von E(r) über eine solche Fläche muß dann Null sein.
Dies ist der Versuch einer anschaulichen Beschreibung des Zusammenhangs.
Die geschlossene Fläche(erkennbar am geschlossenen Integral) ist eine mathematische Oberfläche, die eine geschlossene Kurve(ohne Anfang und Ende) bildet und in sich selbst zurückführt.
Sie kann dabei jede geschlossene Oberflächenform annehmen.
Der elektrische Fluss durch die Oberfläche ist proportional zur eingeschlossenen Ladung.
Elektrische Ladungsdichte:
Gesamtladung:
1/ε weil das elektrische Feld mediumabhängig ist
Erstmal zum Epsilon0. Hier wird offenbar davon ausgegangen, dass es sich um Vakuum handelt. Diese Gleichung gilt aber auch in beliebigen Dielektrika. Daher sollte man allgemein Epsilon schreiben.
Die Gleichung kenne ich etwas anders, da wird das Epsilon in das linke Integral hineinmultipliziert. Statt der Feldstärke E hat man die Verschiebungsflussdichte D und das Epsilon sind wir los.
Rechts wird die Ladungsdichte in einem bestimmten Volumen integriert. Das Ergebnis ist tatsächlich die in diesem Volumen befindliche Ladung Q.
Der Kreis im linken Integral bedeutet, dass über die Hülle A (also die Oberfläche) eben dieses Volumens integriert wird.
Es wird das Skalarprodukt aus Verschiebungsflussdichte D und dem Flächenelenent dA (beide vektoriell) integriert. Das Ergebnis ist der Verschiebungsfluss.
Die Richtung des Vektors dA ist die Richtung des Normalenvektors der Oberfläche an der betrachteten Stelle.
Diese Gleichung besagt also, dass der Verschiebungsfluss durch die Oberfläche eines geschlossenen Volumens gleich der in diesem Volumen eingeschlossenen Ladung ist.
(Gaußscher Satz)