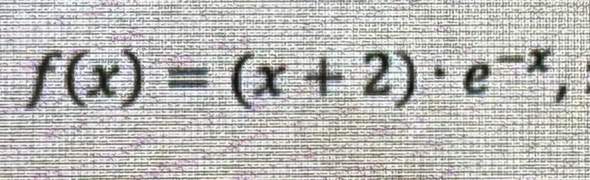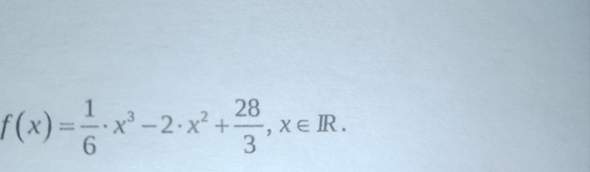Hallo, ich brauche hier dringend bei der Aufgabe Hilfe:
Bei Temperaturen zwischen 15°C und 45°C finden Salmonellen in Lebensmitteln ideale Voraussetzungen für ihr Wachstum. Deshalb sollte man zubereitete Speisen z.B. für eine Party nicht zu lange stehen lassen und schnell im Kühlschrank reintun. Die momentane Wachstumsgeschwindigkeit einer Salmonellenart kann näherungsweise durch die Funktion f beschrieben werden, dabei wird t in Stunden angegeben und f(t) gibt die Anzahl der Salmonellen pro Stunde an.
a) Bestimme 3 Stammfunktionen F von f und erläutere deren Bedeutung für den Sachzusammenhang.
b) Angenommen, eine Speise wird auf einer Party angeboten und enthält zu Beginn (zum Zeitpunkt t=0 ) etwa 600 Salmonellen der oben beschriebenen Art. Gebe die passende Stammfunktion F für diesen Anfangswert an.
c) Berechne mithilfe des Ergebnisses aus b) die Anzahl der Salmonellen in der Speise nach 5 Minuten, 10 Min, 15 Min, 20 Min.
Ich habe jetzt mehrere Fragen: 1. Wozu braucht man hier überhaupt Stammfunktion auszurechnen (na gut, das ist auch Aufgabe a) ) und 2. Was bedeutet hier in der Aufgabe "momentane Wachstumsgeschwindigkeit"?