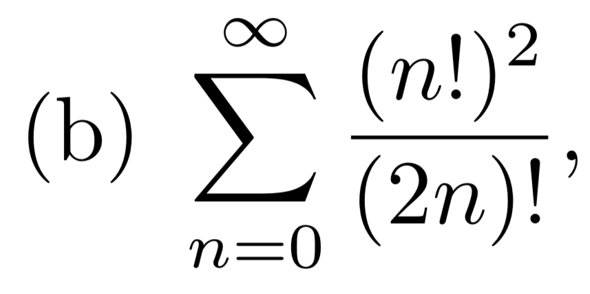Grenzwert – die neusten Beiträge

Guten Tag,

zur Mathematik-Vorlesungsnachbereitung habe ich eine Frage. Es geht um Häufungspunkte von Folgen und Reihen im Rahmen von der Untersuchung von Grenzwerten etc.

Folgende Zusammenfassung habe ich mir selbst geschrieben, die noch sehr schwammig formuliert sein kann und evtl. Fehler aufweist:

"– Häufungspunkte (HP) –

Sei eine Folge an gegeben. Wenn ab einem bestimmten Punkt auf der Zahlengeraden sich die Zahlenwerte der Folgenglieder anhäufen, wobei gilt, dass im Intervall einer Folge: (1-Epsilon. 1+Epsilon) plötzlich alle ab einem gewissen Folgenglied an alle folgenden Folgeglieder in diesem Intervall liegen, so hat die Folge an  hier einen Häufungspunkt. Das Intervall kann hierbei beliebig klein werden. Dann wird irgendwann ein N Element n erreicht sein, sodass alle Folgeglieder im Intervall liegen werden. Erinnern wir uns an diese eine Eigenschaft in Verbindung zu dem Satz von Eudoxos und dem archimedischen Axiom: Epsilon>0 -> n>= 1+ Floorfunktion(1/Epsilon) Element der natürlichen Zahlen im Intervall. Hierbei erkennt man, dass wenn Epsilon kleiner wird, n zwingend größer werden muss!"

Im Vorlesungsskript sind HP folgend definiert: "Ist an Teilmenge von IR eine Folge, so heißt a Element IR Häufungspunkt von an, falls es eine Teilfolge von an gibt, die a als Grenzwert besitzt ".

Müssen wir jede Folge also beim Untersuchen in Teilfolgen splitten, um zu jeder Teilfolge von an ein individuelles a zu finden?

Leider kann ich hier keine mathematische Schreibweise adäquat verwenden.

Hierbei schon eine kleine Frage: Gilt diese mathematische Beschreibung "Epsilon>0 -> n>= 1+ Floorfunktion(1/Epsilon) Element der natürlichen Zahlen im Intervall" nur für Nullfollgen?

Nun ist die Frage, wie bestimmt man durch vollständigen Beweis die Häufungspunkte?

Hierbei ist es auch spannend, da nun bisher folgende Sachen durchgenommen worden sind:

• Häufungspunkt
• Grenzwert
• Cauchy-Folge
• Beschränktheit (Supremum, Infimum, ...)

Kann ich diese verschiedenen Definitionen als jene vielfältige Möglichkeiten verstehen, die es uns ermöglichen, Rückschlüsse auf Konvergenz/Divergenz zu ziehen? Alles führt ja in etwa auf das selbe hinaus, wenn auch manchmal nicht hinreichend genug.

Es handelt sich hierbei nicht um eine Diff/AGLA Vorlesung eines reinen Mathematikstudiums, eventuell unterscheidet sich hierbei die Detailtiefe. Es geht um das Physikstudium deren Mathematiktiefe.

Hallo,

ich habe viele kleine Fragen und wäre sehr dankbar, wenn mir jemand auf all die kleinen Antworten eine Antwort geben könnte. Ich danke sehr!

1.0 Erstmal wollte ich folgende zur Lösungangabe zur Wertemenge fragen:

Ich sehe oft folgendes eckige Klammern die nach außen und nach innen zeigen, also sowas (ich verwende jetzt Mak runde Klammern, weil ich nicht weiß, wie man die eckig macht): ( 5; unendlich(

oder )5;8(

wann werden diese umgedreht und wann nicht?

2.0Auch wollte ich folgendes fragen. Wie sage ich, dass beispielsweise nur die Zahl 2 und 4 für eine Gleichung (Wertemenge) nicht funktionieren und wie sage ich, dass alle Zahlen von 2 bis 4 für den Wertebereich in Frage kommen, also wie kann ich das unterscheiden von der Schreibweise. Ich habe bei beiden immer die Trennung mit einem ; gelesen, wann heißt aber was ?

3.0 Dann eine Frage zu gebrochenen rationalen Funktionen. Ist es grundsätzlich immer so, dass nur die Zahlen für die Definitionsmenge nicht in Frage kommen, die eine Teilung durch 0 "verursachen" würden?

4.0 Ich bin noch nicht so vertraut mit der Grenzwertberechnung und deshalb folgende Frage. Es ist ja beispielsweise so, dass man x gegen einen Grenzwert oder gegen unendlich laufen lässt (von links und von rechts). Mein Taschenrechner erkennt anscheinend, dass ich den Grenzwert berechne und gibt mir den auch an (wenn ich dann auf die jeweillige Lösungen gehe zeigt er mir an, dass dieser eigentlich nicht der des Grenzwertes ist). Meine Frage ist folgende. Kann ich grundsätzlich ausgehen, wenn ein Grenzwert gegeben ist, dass alle anderen reelen Zahlen mögliche Lösungen sind? Habt ihr irgendwelche Tipps wie man herausfinden kann, welche Zahlen für die jeweilige Wertemenge in Frage kommen (habt ihr eine Idee für ein vorgehen)?

ich danke ganz herzlich.

2=sqrt(4)=sqrt((-2)^2)=((-2)^2)^0.5=(-2)^2*0.5=(-2)^1=-2

warum sollte man die dritte potenzregel da net anwenden können?

Hallo! Die Zahlenfolge wäre: 1,1,2,6,24,120.

Ich habe verstanden, dass sich die nächste Zahl immer aus einer natürlichen Zahl und dann dem Produkt der natürlichen Zahl und dessen vorherigem Ergebnis zusammensetzt.

Also:

1*1=1

1*2=2

2*3=6

6*4=24 etc

Nur die erste 1 der Zahlenfolge passt da nicht rein.

Kann mir jemand helfen?

Was ist das Ergebnis von 0,25×3halbe ? Also drei halbe soll ein Bruch sein also 3 im Zähler und 2 im Nenner.

Hallo! Ich hab die folgende Funktion: dN nach dt = -lambda N

Ich verstehe den rot eingekreisten Schritt nicht also wie man vom integral dN nach N auf ln(N) kommt?

Kann mir jemand helfen? Danke

Heute habe ich die erste Mathe LK Arbeit in der MSS geschrieben. Die meisten Aufgaben waren klar und verständlich, jedoch gab es eine aufgabe, die keinen sinn (nach den meisten von uns schülern) ergab, und unsere Lehrerin konnten wir net fragen, weil sie krank war und vertreten wurde.

Die Aufgabe war etwa wie unten, jedoch gab es aus unserer Sicht keine eindeutige Definitionslücke, sondern viele Möglichkeiten und auch keinen Grenzwert! Oder liegen wir da falsch? Kennt sich irgendwer hier damit auf und könnte aufklären, ob vllt unsere Lehrerin auch einen Fehler bei der Erstellung der Kursarbeit gemacht hat?

(Im Unterricht hatten diese Übungen immer einen festen Grenzwert und eindeutige Def.-Lücken)

Ich habe heute folgendes gelesen (bezogen auf Zahlen) "Ausdruck der Stufe" und wollte demnach fragen, was das bedeuten soll. vielleicht Zahlen, die die gleichen Eigenschaften wie die natürlichen Zahlen haben?

Hallo ich würde mich freuen, wenn mir jemand bei dieser Aufgabe helfen kann:

Dankeschön!!

Liegt ein Funktionsgraph immer unterhalb der Geraden mit der Gleichung y = 1 und steigt im ganz reellen Bereich, dann ist der Grenzwert für X → + ∞ gleich 1."

Warum stimmt diese Aussage

Hallo, ich habe mir gerade einige Seiten dazu durchgelesen, aber verstehe es nicht. Ich habe die Aufgabe f(x) = 2x + 3. Setze ich nun Werte in x ein?

Wir sollten das für n=4 und n=8 machen. Denke aber irgendwie, dass ich das falsch gemacht habe. Die Fläche beträgt ja eigentlich 1/3.

Hallo zusammen

Kann mir jemand die folgenden Aufgaben erklären. Ich habe es versucht und auch in meinem Unterlagen und Notizen geschaut, jedoch nichts passendes gefunden. Ich habe so gar keinen Ansatz... :(

Ich danke schonmal im voraus...

Hey, ich hab eine Mathe Hausaufgabe auf die ich nicht so Recht verstehe.

Kann mir bitte jemand helfen. Ich soll diese Aufgabe machen.

Danke schonmal im voraus.

Ich komme hier im Selbststudium irgendwie nicht weiter. Ich finde einfach kein Verfahren, dass für jede dieser Art von Aufgaben funktioniert.

Ich weiß nicht genau wie ich bei solchen Aufgaben auf Stetigkeit untersuche.

Habe Lösungsansätze mit Polarkoordinaten oder Folgen der Art 1/k gesehen aber auch Lösungsansätze wo ein Gegenbeispiel gefunden wurde um Unstetigkeit zu zeigen.

Wäre lieb wenn mir jemand weiterhelfen könnte. Reicht auch wenn mir jemand ein gutes Video verlinkt oder einfach das Verfahren kurz erläutert wie man solche Aufgaben löst.

LG :)

Hallo,

Ich habe mir folgende Frage gestellt:

Man nehme einen Wert n, welcher zu 0 konvergiert. Man multipliziere diesen Wert n mit Unendlich (bzw. der Unendlichkeit).

Wäre es in einer vorstellbaren Kombination möglich, den Wert 1 zu erreichen? Eigentlich wäre Unendlich multipliziert mit einem beliebigen Wert ebenfalls Unendlich, doch wie verhält es sich einen endlos großen Wert mit einem endlos kleinen (positiven) Wert zu multiplizieren?

Es wurden dazu schon verschiedene intelligente Menschen, eine Physiklehrkraft, sowie ChatGPT o1 Preview befragt. Eine einleuchtende Antwort konnte bislang niemand geben.

Liebe Grüße,

Euer anonymes Fragenhörnchen mit dem schwarzen Balken vor den Augen, den GuteFrage irgendwie auf mein Gesicht geklebt hat ^^

Ich weiß, wie man epsilon berechnet

Das 2 Beispiel hab ich dann selber gemacht

Bitte

Hey, kann mir hier jemand weiterhelfen?
Ich verstehe die Aufgabe leider nicht.

Danke im Voraus :)

frage steht oben.

Also wieso ist Stetigkeit eine notwendige Bedingung für diffbarkeit wenn die Ableitung an der stelle gleich ist???

Mein Thema in Mathe ist ist rekursive Zahlung Folge

Die Zahlung Folge lautet 1024, 512, 256 ,128, 64,32,
Die Lösung lautet an+1=an:2

Was ist? Ich dachte aber : an= an-1:2

Langsam bin ich verzweifelt und versteh nicht, wie man auf die Form dieser Zahlung Folge kommt

Die Zahlung Folge lautet 2, 3, 5,8, 13,21

die Lösung lautet : an+1 =an+an-1

allein meine erste Frage bei dieser Form lautet, warum an+1 am Anfang steht statt an=

Hallo,

ich lerne gerade für eine Arbeit und habe keine Ahnung wie man hier die Gleichung bestimmen soll.

Ich hatte für a) -40,5/-3^n in die Gleichung von -8=-40,5/-3^n *2^n eingesetzt, jedoch kam ich dann an das Problem, dass ich den Logarithmus(wie ich es immer gemacht habe)anwenden wollte, aber der Logarithmus ja nicht von einer negativen Zahl definiert ist.

Ist die Aufgabe falsch oder wie kann man das anders rechnen?

Die zehn Folge lautet 0 2 6 12 20 30

Hier wird immer n immer +2 gemacht, das hab ich verstanden die Lösung lautet an= an-1 +2(n-1) ich dachte an=an-1+n+2 jedoch ist das falsch, was ich nicht verstehe, weil n wird ja immer mit zwei addiert

Bei der arithmetische zahlengolge die Folgen lauten 5 6 8 11 15 und 20 die Lösung ist an-1+n-1 ich verstehe nicht warum n-1 statt n+1 weil n wird ja immer mehr

Die linke Teilfolge konvergiert ja gegen 0 und die rechte gegen unendlich. Das heißt doch, dass es eine konvergente Teilfolge gibt?

Ich hab in Mathe ein Arbeitsblatt bekommen mit den verschiedenen Funktionstypen und dort hab ich mir bereits die funktionsterme der Abbildungen und die allgemeinen Funktionsterme erarbeitet bzw. wiederholt. Nun ist das neue Thema den Grenzwert zu berechnen, und wir haben als Hausaufgabe bekommen dieses Arbeitsblatt auszufüllen.

jetzt bin ich mir jedoch nicht sicher welche Typen konvergieren ( bis auf die gebrochen rationale Funktion da weis ich dass die asymptote der Grenzwert ist weil sich ja der Graph immer weiter annähert aber nicht berührt)

Ist 0 ungleich 0?

Kann man beweisen, dass 0 ungleich 0 ist ?

Ich habe eine Theorie, dass die Wahrheit und Lüge dasselbe in andere Form ist. Dann ist nicht alles so wie es scheint.

Ich komme darauf weil ich mich Frage Warum die Welt oder der Gott der Sie geschaffen hat ohne Ursprung existiert. Was auf eine Widersprüchliche Existenz zurückzuführen ist. Das bedeutet 0 ist ungleich 0

Und 1 = -1 (ungleich 0)

Es gibt Komplexe Zahlen und Formeln kann man beweisen das Lüge und Wahrheit dasselbe in anderer Form sind ?

Wie Albert Einstein mit seiner Berühmten Formel: E=MC^2 (Energie und Masse sind dasselbe in anderer Form)

Die Welt ist nur scheinbar und Widersprüchlich. Doch ist der Widerspruch kein Widerspruch da die Grundlage der Logik im Widerspruch steht

Ich soll eine rekursive Formeln für diese Zahl folge bilden ich versteh die Lösung nicht

5 6 8 11 15 20

Die Lösung ist : an-1 + n-1. a1=5

 f (x)= x² -1/x(x-1) geteilt sollte ein Bruchstrich sein.

Wo ich mir jetzt nicht sicher bin, das x vor der () wird x²-1/x?

und dann kann ich beide x² kürzen und das Ergebnis ist dann -1?

Ich möchte zur Übung von folgender Folge den Grenzwert berechnen, mit l Hopital komm ich irgendwie nicht weiter....muss ich Taylorn? laut Lösung ist es 1/2, jedoch ist kein Rechenweg vorhanden.

a) f ( x)= 2 x+x2 x2

2x+x² geteilt durch x²

Wie wir das berechnet mit Lösungsweg?

Als Hausaufgabe haben wir aufbekommen den rechenweg zu erklären.
Bei der Berechnung der Un und On weisst ich nicht so genau, wie die auf den Ergebnis kamen. Bei der Grenzwertbildung auch nicht.

Einige sagen, es ist -unendlich, einige, dass er nichtdefiniert ist - beides kommt mir irgendwie logisch vor. Man kann eigentlich keine negativen Zahlen für x einsetzen aber wenn man sich die Funktion an einem Graphen anschaut bin ich mir schon nicht mehr so sicher…

Vollständige Induktion,

Hallo,

Ich habe mich wieder mit dem Prinzip der vollständigen Induktion befasst und habe folgenden Denkfehler: Am Anfang gibt es ja eine Behauptung, die man durch das Einsetzen einer Zahl beweist. Das bedeutet ja, dass man ab diesem Moment sagt, dass die Gleichung XY für eine bestimmte Variable (natürliche Zahl) gilt. Sagen wir Mal, die Voraussetzung ist, dass es beispielsweise für n 1 gilt. Dann setzt man für n, (n + 1) ein und beweist hiermit unter der Voraussetzung, dass die Gleichung für n=1 erfüllbar war, dass die Gleichung auch für den Nachfolger, also zwei erfüllbar ist.

Ab hier habe ich eine Frage: Üblicherweise hört man ja hier auf (die Annahme, dass es für alle natürlichen Zahlen gilt, ist bewiesen). Liegt es hierbei daran, dass wenn man zeigt (durch Umformungen etc), dass man n+1 auf der „anderen“ Seite rekonstruieren kann, dass auch n+2, also auch n+3 n+4 ..-…. rekonstruierbar ist? Oder wie versteht man das? Würde das also auch bedeuten, dass wenn ich (n-1) beweise, dass auch (n-2..) gilt?

Zudem: Verstehe ich das richtig, dass die vollständige Induktion also einer Art Beweissatz ist, der die „Gültigkeit“ einer Lösungsmenge darlegt?

Gibt es eine Möglichkeit nur mit der vollständigen Induktion zu beweisen, für welche Zahlenmengen eine Gleichung gilt (also ohne davor eine Voraussetzung zu haben, dass beispielsweise Gleichung XY für alle natürlichen Zahlen gilt)?

Hallo!

Folgendes ist die Aufgabe:

,

wobei wir die stetige diff'barkeit zeigen sollen.

Mein Ansatz:

Ich habe mir erstmal den Fall für x in dem Intervall -1,1 angeschaut und die Ableitung "ausgerechnet" mithilfe der Kettenregel, da ja 1/C eine konstante ist.

Nun bin ich auch gerade dabei das für x nicht in dem Intervall zu zeigen, aber da komme ich nicht weiter:

Wie wäre euer Ansatz/wie würdet ihr da weiter rechnen?

Georg Cantor hat bewiesen, dass die Menge der reellen Zahlen im Intervall [0;1] nicht bijektiv zur Menge aller natürlichen Zahlen ist. Dies tat er durch sein Diagonalargument. (Ich weiß grad nicht mehr, ob das erste oder zweite.)

Aaaaber ich verstehe nicht, warum keine Bijektion herrscht, nur weil die Liste nie vollständig ist. Denn lediglich das zeigt Cantors Argument.

Eine Liste von unendlichen Zahlen, ist ja sowieso niemals vollständig.

Nur weil bewiesen werden kann, dass die Liste nicht vollständig ist, heißt das nicht, dass es keine eineindeutige Zuordnung der Elemente geben kann. Oder etwa doch? Aber warum?!

Bei den geraden Zahlen geht das ja auch, obwohl man immer wieder eine neue Zahl erschaffen kann. (Die letzte +2)

Warum darf er überhaupt seine These auf unendlich lange Zahlen machen? Man kann doch nicht alles einfach in die Unendlichkeit übertragen. Sein Argument ergibt ja einigermaßen Sinn, aber doch nicht für unendlich lange Zahlen, die ja aber damit erschaffen werden!

Ich verstehe echt nicht den Zusammenhang zwischen einer immer unvollständigen Liste einer Menge und ihrer Bijektion und warum sein Argument für unendliche Längen überhaupt erlaubt ist.

Habe diese Folge cn := (−1)^(n+1)

(6n^2

13n)/ 5n^3 + 7) gibt es hier keine obere Schranke,

der absolut betrag bei n=1 wäre ja zum Beispiel 19/12 dann fällt ja der absolut Betrag bei n=3 usw

Die Folge ist alternierend klar , Häufungspunkt 0 , aber ist nicht der höchste Wert 19/12 somit das Supremum ?

Kann mir jemand helfen, wie man das berechnet? Ich hab‘s in der Schule nicht verstanden, aber achreibe morgen eine Arbeit

Woher weiß er bei Verhalten der Ränder, dass es eine Minimalstelle geben muss wenn von rechts gegen 0 auf unendlich wandert und x gegen unendlich auch gegen unendlich wandert ?

Woran macht er es fest ?

und wenn man das festgestellt hat das es ein minimalstelle ist braucht man nicht die 2 ableitung wie er es gemacht hat oder hat er bewusst die 2 ableitung weggelassen weil es ehh nur 1 Punkt gibt und wir wissen das es ein minimalstelle sein muss?

1) Bild

2) Bild

Das erste Bild ist ja offensichtlich für die Reihen nur gedacht aber das 2 Bild ?

Gild die Regel beim 2 Bild nur für Folgen ?

(1/4^n) kann man ja schreiben als (1/4)^n und dann kann man ja die geometrische reihe anwenden 1/1-q = 4/3 ist.

Aber (1/4^n) zu (1/4)^n gilt nur weil zähler 1 ist und wenn es z.B > 1 ist dann geht es nicht?

2/4^n != (2/4)^n ? weil dann kommen ja unterschiedliche Zahlen raus wenn n z.B 3 ist

Bräuchte eine Funktion die 0 ergibt, sobald ein negativer Wert rauskommt.

Ich grübel derzeit ein wenig über die Lösung, die meine Professorin bereitstellt. Unzwar folgende:

Warum kann ich von 2n+2n+1 zu 2n+2 schließen? Bitte einfach erklärt mit ggf. einem Beispiel.

Ich selbst hab die Aufgabe etwas anders bearbeitet:

Was ich gemacht habe:

ich habe (n+1)^2 ausgeklammert, dann hab ich mir eine 1 dazugetan, damit ich auf die form (2n+2) + 2n-1 komme und dann mache ich die kleine Abschätzung, dass 2n-1 immer größer gleich 0 sein muss, da n>=2 und im IS steht 2n+2+0

Hab ich das richtig gemacht? Zumindest ist das so, wie das von Daniel Jung gezeigt wird und vielen anderen

Unten im Bild ist eine Konvergenzradiusaufgabe zu sehen aus dem Klausurtraining für unsere hm1 Klausur.

Der Weg über das Wurzelkriterium den Radius zu bestimmen hat mich nicht weitergebracht.

Beim Quotientenkriterium habe ich das Problem, dass ich die Fakultät nicht loswerde. Kann mir vielleicht jemand einen Tipp geben, wo ich etwas übersehe. Durch Wolfram Alpha weiss ich, dass eine Lösung ohne Fakultät existiert.

Ayo.. ich habe irgendwie immer Problem damit zu verstehen wie Grenzwerte wirklich Funktionieren.

Es ist auch ein wenig peinlich es immer noch nicht zu verstehen, allerdings würde ich es gerne verstehen aber kriege es nicht hin.

Mein Problem ist, dass ich nicht wirklich verstehe wie sich eine Funktion verhält wenn es gegen 0 oder gegen unendlich geht.

Hier ein Beispiel

Hier kannan zum Beispiel L'Hospital verwenden weil es gegen 0/0 geht. Danach kann man ja ableiten etc. und danach kommt zum Schluss 1 raus.

Aber da sowas ich nie verstehe ist warum (e^x-1)/x gegen 0/0 gehen soll. Also ich verstehe nicht wirklich wie es mir vorstellen soll, wenn etwas (hier x) gegen 0 laufen soll und warum es hier 0/0 ergibt.

Wie kann man es schnell erkennen bzw wie muss ich dieses Verhalten (gegen was es geht) verstehen?. Kann mir jemand es einfacher erklären?

ist x^2 / |x| in x=0 stetig fortsetztbar ?

also lim links und rechts sind beide 0 dann kann ich doch die funktion bei x=0 mit 0 definieren oder?

lim x --> π für 

π kann man nicht einsetzen, da der Punkt dort unstetig ist. Wie kann ich also näherungsweise den Grenzwert der Funktio herausfinden, wenn x gegen π geht?

Also hier steht, der Limes von tan(x/2) bei x --> π sei 1

Wie kommt man darauf? Bei tan(π/2) ist ja ein Unstetigkeitspunkt. Wie kann ich annäherend den Limes denn herausfinden?

Die Zahl Pi ist ja unendlich, aber gleichzeitig kleiner als 3.2

Wie kann das sein

Wie kann ich eigentlich intelligenter werden? Ich habe immer in meinen Leben das Gefühl gehabt das ich einfach unglaublich dumm bin.

Es ist einfach scheiße, dumm zu sein und nichts verstehen zu können. Selbst für die Themen für die ich sich interessiere bin ich eine versagerin. Ich löse ständig Probleme falsch, ich kapiere absolut garnichts wenn man mir versucht was zu erklären..

Ich muss jeden Tag Chat gpt benutzen weil ich simplere Aufgaben einfach nicht verstehe und Chat gpt die ganze Zeit mit fragen bombardieren muss was damit gemeint ist.

Bei den ganzen Lehrbücher checke ich absolut garnichts. Und niemand kriegt es vernünftig hin mir irgendwelche Themen zu erklären..

Ich bin nicht mal vernünftig in der Lage für eine Klausur zu lernen, da mein scheiß Gehirn alles wieder vergisst. Das ist einfach scheiße. Und selbst wenn ich irgendwas verstehen würde, dann auch nur zufällig (unabhängig vom lernen oder nicht).

Mein Gedächtnis ist ebenfalls scheiße asf...

Im Studium schaffe ich nicht mal irgendwelche Klausuren! Was unglaublich scheiße ist, weil mein Fach eigentlich sehr liebe, aber ich habe nur Probleme.

Ich schecke z.B bis heute nicht wie das berechnen von Grenzewerten funktioniert. Ich weiß es gibt sowas wie L'Hospital und das kann man anwenden wenn der Grenzen gegen 0/0 etc.. aber z.B mein problem..

ich schecke einfach nicht wie ich es verstehen soll das z.b "n" gegen unendlich (oder 0) geht und wie es sich auf die ganze Funktion Auswirkt...oder z.b das wenn es fü n gegen unendlich gehen, gehen diese und diese variabeln gegen 0... Ich verstehe es einfach nicht wie ich es mir logisch herleiten soll.

Zusätzlich ist mein Problem dadurch noch größer, weil ich ADS und Asperger habe

Also zurück zu meiner eigentlichen Frage? Wie kann ich intelligenter werden und vor allem ein besseren Gedächtnis bekommen?

Ich weiß viele sagen, Ernährung ... Aber das bringt ebenfalls garnichts bei mir. Egal was ich esse, a mein Gehirn und körper ändert sich nicht.. schlafen tue ich auch ca.6 bis 8 Stunden.

Also was ist falsch mir meinen scheiß Hirn?

Mein Ergebnis wäre die Reihe ist Konvergenz

Wieso werden hier die unteren Integralgrenzen durch einen Buchstaben ersetzt und wieso geht x gegen die angebeben "Werte"? Wie kommt man darauf?

Hallo zusammen,

und zwar will ich den Grenzwert bestimmen. Also setze ich für ln(0) und für cot(0) ein, beides ergibt Error im Taschenrechner. Das heißt doch, dass ich nicht mal die Regel von L'Hospital nutzen kann, oder habe ich einen Denkfehler?

Hallo, kann mir jemand erklären wie ich bei Matlab Grenzwerte bestimmen kann...

Meine Lehrerin sagt, dass sobald ein Term nicht gegen 0 strebt ist er sofort als divergent zu bewerten, aber im Internet steht, dass konvergent gegen irgendeinen streben bedeutet z.B. kann dieser Wert auch 1 sein - wer hat Recht?

Außerdem warum benutzt man wenn es um absolute Konvergenz geht immer den Betrag?

Ich bin verwirrt. Ist die Gleichung erfüllt wie bsp. 0•x3=0 dann ist die Lösungmenge unendlich wie es auch bei mir im Buch steht.

Und bei mir oben kommt ja -1x3=-1 raus. Wieso ist die Lösungsmenge aber nicht unendlich? Könnte mir da jemand bitte helfen?

(die Lösung ist richtig, ich versteh nur nicht wieso die Lösungsmenge nicht unendlich ist)

DIE GRENZEN DER AI

Sicherlich gibt es Beispiele wo die kuenstliche Intelligenz an ihre Grenzen gelangt. Gerne wuerde ich Beispiele wissen, wo sich AI nicht anwenden laeest.

Nachfolgende Situatiin aus meiner fruehen Kimdheit fasziniert mich sehr und regt mich immer wieder an ...

Mein Vater hat mit grosser Hingabe die Apfelbaeume im eigenen Garten am Haus gepflegt. Vielfach wurde sein unermuedlicher Einsatz mit guter Ernte belohnt.

Ein wichtiger Bestandteil war auch der Winterschnitt im unbelaubten Zustand. Meine Hilfe bestand zu dieser Zeit ueberwiegend vom Aufsammeln des Schnittgutes und Erlernen der Wuchsgesetze der einzelnen Apfelbaeume fuer die spaeter auf mich uebergehende Aufgabe.

Auf eine Anfrage, ob er denn auch die Baeume fuer jemand anderen schneiden koennte, entgegnete er freundlich, dass man doch die Baeume vorbeibringen sollte ...

Ich war damals noch ein kleines Kind, hatte die Antwort / den beabsichtigten Sinn seiner Antwort ueberhaupt nicht verstanden ... und fragte nach dem Abendessen was er den gemeint hatte ...

Liebevoll hat er mich hingefuehrt, dass ich die Antwort mir "erarbeiten" konnte.

Je mehr wir von "AI" im Alltag beeinflusst sind, um so faszinierender finde ich die Antwort, die er damals gegeben hat ...

... und fuer mich, noch heute, das gelegentlich bewusste Suchen nach Grenzen, wo die "modernenTechnologien" - AI - NICHT anwendbar sind, und ich den Begriff Intelligenz immer mehr in Frage stelle ...

Gerne moechte ich weitere Beispiele ...

Wie mache ich d? Y=0 ist ja die asymptote

Hallo liebe Community,

gegeben ist folgende Funktion:

Zu dieser Funktion wurde als Grenzwert die Gaußsche Glockenkurve mit e^1/2*x^2 gefunden. Da die Funktion allerdings noch integriert wird, gilt dieser Grenzwert ja nicht zwangsläufig mit dem Integral weshalb dominierte Konvergenz verwendet wurde. Die Majorante dazu war:

Und dann wurde folgendes gemacht, was ich nicht ganz verstehe:

anscheinend wurde durch Monotonieverhalten gezeigt, warum die Funktion immer kleiner als die Majorante ist, aber das verstehe ich nicht ganz. Kann mir bitte jemand erklären was auf den letzten beiden Fotos passiert ist?

Lg

Wie bekomme ich hier die asymptoten?

Wie löse ich x^5 =230 mit dem ln?

Guten Nachmittag!

ich wollte mal nachfragen, warum man am Ende der h-Methode eine null ins h setz, was ist die Idee dahinter ?

Hallo liebe Community,

Ich soll im Rahmen meines Studiums die folgende Aufgabe lösen:

Komm dort aber relativ schnell nicht wirklich voran. Hier mein bisheriger Lösungsansatz:

Wir suchen:

 Zunächst betrachten wir exp(A+tB).

  Wir lassen ja t gegen null gehen. Multipliziert man exp(A+tB) vollständig aus, so erhält man viele Summanden, in denen t zu einer Potenz von 2 oder höher vorkommt. Davon kürzt sich ein t mit dem Nenner, der Rest läuft gegen 0, wodurch der ganze Summand 0 wird. Wir müssen also nur jene betrachten, für die die Potenz von t eins oder 0 ist.

    Ich komme bis zu dieser Reihe. Kann ich die noch weiter zusammenfassen? Ich sehe wenn ja, leider nicht wie. Aber in dieser Form sieht es sehr unschön aus. Es muss doch einfacher gehen. Ich habe ja dann quasi:



Hallo,

gegeben ist folgende Funktion

Mit folgenden Ableitungen

Darauf soll nun der Satz von Taylor angewendet werden. Dabei wurde folgendes formuliert:

Und das verstehe ich nicht. Warum muss n größer x^2 sein, bzw. woher kommt das? Es wäre doch sicherlich möglich das n irgendwie anders zu wählen, oder?

Lg

Kann mir jemand die Theorie dahinter erklären?

LG :)

Das bisherige absolute Verbot, unter Einfluss von Cannabis Auto zu fahren, gilt vorerst fort. Ein konkreter Grenzwert wie von der Expertenkommission jetzt vorgeschlagen oder wie 0,5 Promille bei Alkohol steht bisher nicht im Gesetz.

Allerdings ist jetzt bekannt welcher Grenzwert vermutlich kommen wird.

In der Empfehlung an das Verkehrsministerium heißt es: "Bei Erreichen dieses THC-Grenzwertes ist nach dem aktuellen Stand der Wissenschaft eine verkehrssicherheitsrelevante Wirkung beim Führen eines Kraftfahrzeuges nicht fernliegend." Das heißt, es kann ab diesem Wert womöglich von einer Wirkung ausgegangen werden.

Das Bundesverkehrsministerium ergänzt: "Bei dem vorgeschlagenen Grenzwert von 3,5 Nanogramm THC im Blutserum handelt es sich nach Ansicht der Experten um einen konservativen Ansatz, der vom Risiko vergleichbar sei mit einer Blutalkoholkonzentration von 0,2 Promille."

Quelle: https://www.tagesschau.de/inland/cannabis-verkehr-100.html

Ergibt minus unendlich^2 gleich unendlich?
oder falls nicht, was genau kommt dabei raus?

[Bild entfernt]

Uni in Dortmund:

Aufgabenstellung: Finden sie heraus welchen grenzwert die reihe hat

danke für die hilfe

Guten Abend!

Ich habe hier versucht die Monotonie zu untersuchen in dem ich die erste Ableitung bilde um ihre Nullstellen berechnen ,um den Monotonie verhalten untersuchen zu können. Jedoch hat die Funktion anscheinend keine Nullstellen.

Kann ich hier einfach direkt davon ausgehen das die Funktion streng monoton steigend ist ,weil sie eine Funktion 3 Grades ist und einen positiven Vorzeichen besitzt?

Kann mir jemand kurz erklären ob diese Grenzwerte vorkommen können oder nicht und warum?

Habe da gerade noch Verständnisprobleme.

(meine Lösungen sind nur geraten)

Ich habe für meine Übungsaufgaben diesmal folgende Aufgabe zu lösen:

Ich hätte dies mit dem Folgenkriterium gelöst, bin mir aber nicht sicher, ob das so geht.

 Wir nehmen das Gegenteil an, und führen einen Widerspruchsbeweis.

 für irgendein Epsilon > 0.

Wir bezeichnen die Menge dieser "Verräter" als M. Nun bilden wir eine Menge in X:

 Mir fällt auf: Das ist ein bisschen falsch geschrieben. Ich meine konkret: Wir wählen eine Folge aus jenen f^-1(yn), die in M sind. Insbesondere ist x_n immernoch Teilfolge von f^-1(yn).

Aber es gilt:

 Nun betrachten wir aber mal f(x_(n_k)).  Gleichzeitig gilt aber auch:

  Und das ist der Widerspruch, da (x_n) ja gerade so gewählt wurde, dass alle x_n mindestens Epsilon-weit davon entfernt sind.

Hallo,

ich muss eine Partielle Ableitung ausrechnen

 , allerdings würde ich dann ja, wenn ich für h=0 einsetze, durch Null teilen, was ja nicht geht. Stimmt das, dass ich, wenn diese Gefahr für h=0 bei einer umgeformten/äquivalenten Gleichung nicht besteht, "einfach" den Grenzwert für h, also Null, einsetzen könnte und damit den Grenzwert berechnen kann?

Danke im Voraus!

Was I+I



Warum sagt der Dr. Gitt hier: 80 durch Unendlich?

Es sollte eigentlich umgekehrt sein, oder?

Damit man die Länge der Unendlichkeit begreift, sollte man Unendlich durch 80 teilen.

Ich verstehe es nicht. 😌 Bitte erklären.

https://www.youtube.com/shorts/uvz915ntLA4

wenn man den grenzwert/limes ausrechnet von ♾️ und man dann „♾️“/ „♾️“ hat. ist dann der grenzwert ♾️ oder 1

Z.b f(x) =x/|x| ist bei x0 =0

da komme ich auf den Grenzwert von rechts auf 1 und von links auf -1 falls das richtig ist wäre die Funktion an dieser Stelle nicht stetig . Da die Funktion aber in 0 nicht definiert ist könnte man sie doch an dieser Stelle fortsetzt bar machen oder ?
Ich hätte gesagt mit der ,,neuen Funktion‘‘ f(x)=x/|x| für x ≠0 und 0 für x=0

ach und falls das richtig sein sollte wäre nett wenn ihr ein weiteres schwierigeres bsp zeigen könnte wo man eine Funktion stetig fortsetzbar machen kann

Ich verstehe nicht ganz wann eine Funktion nur linksstetig bzw rechtsstetig ist ?
Bei Stetigkeit berechne ich allgemein den Limes von rechts und links ,sind die Werte gleich dann ist die Funktion an der Stelle stetig. Aber wann ist es nur rechts bzw linksstetig mit was vergleiche ich da meinen funktionswert ?

Hallo, ich hätte eine Frage.

Ist eine Funktion auch dann surjektiv, wenn potenziell mehr Werte angenommen werden können, als der Wertebereich vorgibt? Surjektivität bedeutet ja, dass für jedes y aus dem Wertebereich ein x aus dem Definitionsbereich existiert. Das wäre ja auch gegeben, wenn die Funktion mehr y Werte liefert als erlaubt?

Bspw. f(x) = x^2 ist ja surjektiv für R --> R

wäre f(x) = x^2 noch immer surjektiv für R --> N ? Es würden ja alle natürlichen Zahlen erreicht werden, nur eben noch mehr als diese, wenn man alle Reellen Zahlen einsetzen darf.

Guten Tag, ich habe ein Privatrezept für Cannabis von meinem Arzt ausgestellt bekommen. Wie verhält sich das mit der Teilnahme am Straßenverkehr?

Darf ich nach Einnahme meiner Medizin Auto fahren, muss ich danach eine gewisse Zeit warten oder darf ich garnicht fahren?

Wie sind die gesetzlichen Regelungen diesbezüglich, da ich es ja nicht als Rauschmittel, sondern als Medikament konsumiere.

Grüße Moritz

ist der ggT von 0 und 0 unendlich? weil ich kann ja 0 durch jede zahl restlos teilen, und da der größte gesucht wird, komm ich doch auf die höchste mögliche zahl eines körpers, im fall der Ganzen Zahlen würde der ggT dann ja gegen unendlich streben ... oder hab ich da einen Fehler?

Wie kann ich das zeigen, dass es gegen unendlich geht?
Mir fällt nämlich wirklich nichts ein, außer grafisch zu begründen .



Ich meine der Unterschied ist

1/(n-1), warum macht man überhaupt n - 1?