Mathematisches Problem (Definitionslücken, Grenzwerte)?
Heute habe ich die erste Mathe LK Arbeit in der MSS geschrieben. Die meisten Aufgaben waren klar und verständlich, jedoch gab es eine aufgabe, die keinen sinn (nach den meisten von uns schülern) ergab, und unsere Lehrerin konnten wir net fragen, weil sie krank war und vertreten wurde.
Die Aufgabe war etwa wie unten, jedoch gab es aus unserer Sicht keine eindeutige Definitionslücke, sondern viele Möglichkeiten und auch keinen Grenzwert! Oder liegen wir da falsch? Kennt sich irgendwer hier damit auf und könnte aufklären, ob vllt unsere Lehrerin auch einen Fehler bei der Erstellung der Kursarbeit gemacht hat?
(Im Unterricht hatten diese Übungen immer einen festen Grenzwert und eindeutige Def.-Lücken)

3 Antworten
Ich verstehe nicht so ganz das Problem.
Es gibt zwei Definitionslücken, die beiden Werte, an denen der Nenner Null wird.
Eine der Defintionslücken lässt sich beheben, d.h. es existiert ein Limit. Bei der anderen konvergiert die Funktion, die sich an dieser Lücke asympotisch verhält.
Das Limit für x→+∞ (bzw. x→-∞) ist einfach +∞ (bzw. -∞).
Du kannst das damit begründen, dass der höchste x-Grad im Zähler größer ist als im Nenner, x³ vs. x² bzw. x² vs x nach dem Kürzen und die Funktion somit gegen Unendlich geht. (Es gibt auch kein Vorzeichen, das aus dem plus Unendlich ein minus Unendlich machen würde oder umgekehrt.)
Etwas formaler kannst du das zeigen, indem du den Zähler so umformst, dass du den Bruch derart in verschiedene Brüche zerlegen kannst, dass das Verhalten am Limit* eindeutig wird:
Und hier kannst du jetzt jedes Limit separat betrachte:
lim x geht für x→±∞ natürlich gegen ±∞; lim 1 ist 1 (da von x unabhängig) und lim 7/(x-1) geht für x→±∞ gegen 0.
Du hast für den Gesamtterm also ein Limit von ±∞+1+0. Die 1 kann man ignorieren, die 0 sowieso, also ist das Limit +∞ oder -∞.
Aber vermutlich ist diese ganze Rechnung nicht nötig, da der Hinweis auf den höheren Grad ausreichen sollte.
Was die Rechnung aber doch hergibt, ist dass man zeigen kann, dass sich der Graph beliebig nahe an die Gerade x+1 annähert, wenn die x-Werte sehr groß oder sehr klein werden.
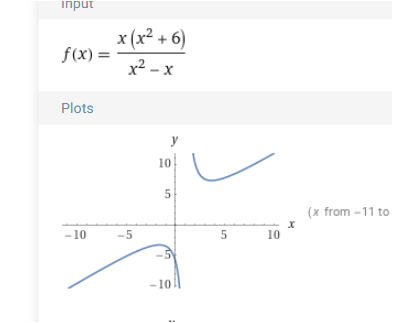
Man sieht das schon ein bisschen in dem Bild, das Halbrecht gepostet hat und es wird noch deutlicher, wenn du dir den Graph auf dem zweiten Bild anschaust, bei dem etwas "herausgezoomt" wird und der Graph bis auf die asymptotische Stelle nahezu wie eine lineare Funktion aussieht.
* ich hab das nicht hingebracht, unter das Limit ein x→±∞ zu schreiben; das musst du dir bei jedem Limit dazu denken. 😉
Auch bei der gezeigten Aufgabe hast du eine eindeutige Definitionslücke. Sie liegt dort, wo der Nenner des Funktionsausdrucks 0 wird. Um herauszufinden, wo der Nenner = wird, löst du die quadratische Gleichung
Dafür brauchst du hier keine pq-Formel; es reicht, x auszuklammern und den Satz vom Nullprodukt anzuwenden.
Wenn du aus dem Nenner x aus geklammert hast, kannst du den Funktionsausdruck mit x kürzen. Den gekürzten Funktionsausdruck verwendest du für die Bestimmung der gesuchten Grenzwerte. Behalte im Auge, dass die Grenzwerte nicht endlich zu sein brauchen.
Um das Verhalten der Funktion in der Nähe der Definitionslücke zu ermitteln, ist der linksseitige und der rechtsseitige Grenzwert an der Lückenstelle zu bestimmen.
Das verwirrende war, dass in der originalen Aufgabenstellung von 2 Definitionslücken die Rede war und wir auch im Unterricht solch ein beispiel mit 2 Def.Lücken hatten (die aufgabenstellung im bild ist nur grob immitiert) Hab das Grundprinzip völlig verstanden, jedoch konnte ich für dieses Beispiel weder den Grenzwert so ermitteln, wie wir es im Unterricht gemacht haben, noch die Definitionslücke bestimmen.
x = +1 ist doch eine eindeutige
x = 0 kürzt sich raus
.
Nach kürzen bleibt
x²+6/x-1
es gilt x²/x zu betrachten
daher rechts + und links - unend.
.
Warum habt ihr die Fkt nicht mal geplottet ?

.
f(x) = (x*(x²+6))/(x²-x)