Kreisbewegung – die neusten Beiträge

Ich brauche eure Hilfe, bitte!:)

Ihr sieht die Frage im Betreff und die Aufgabenstellung als Bild.

danke!

n ist eine beliebige natürliche Zahl

Bitte nur die Antwort und nicht die Begründung schreiben. Angeblich wird diese Frage von den meisten Studenten technischer Fächer falsch beantwortet, was ich mir nur schwer vorstellen kann. Deshalb will ich einfach mal sehen, was hier dabei herauskommt.

Die Auflösung schreibe ich später.

Spoiler: Definition einer Drehung in der Geometrie.

Hi,

was muss ich bei der unten stehenden Aufgabe 2 machen?

Ich habe bereits Aufgabe a und b gelöst, komme jedoch nicht auf den Lösungsansatz bzw. die benötigte Formel für Aufgabe c. Kann mir da jemand weiterhelfen?

Ich habe in Physik das Thema Kreisbewegung und bin bei der Zentripetalbeschleunigung auf folgendes Verständnisproblem gestoßen: Bei der ja vorliegenden gleichförmigen Kreisbewegung ist v konstant, d.h. keine Geschwindigkeitsänderung und somit eigentlich keine Beschleunigung. Jedoch lerne ich über die Zentripetalbeschleunigung. Warum existiert sie, bzw. was beschleunigt da in Richtung Kreismittelpunkt?

Wozu überhöht man zum Beispiel die linke Schiene? Ich mein dadurch verteilen sie die Kräfte besser und die Schienen werden nicht so schnell belastet, aber welche Kraft wird damit ausgeglichen? Kann man sagen, dass durch die Neigung die Gewichtskraft in eine senkrechte und horizontale Komponente geteilt wird und man durch die Überhöhung es schafft, dass ein größerer Teil der Zentripetalkraft durch die Gewichtskraft erzeugt wird und nicht durch die Schienenkraft...Kann mir das jemand bitte erklären?

Erreicht die Geschwindigkeit dort ihr Maximum oder was ?

Welche Kräfte wirken am Anfang eines Loopings? Wir haben die Gewichtskraft und die Normalkraft, die Vektoriell addiert die Zentripetalkraft ergibt? Aber wo sind die Maximalpunkte? Ist die Zentripetalkraft am obersten Punkt am größten und warum ?

Hey versteht jemand die b? Ich mein die Zentripetalkraft wirkt nach unten, bloß frag ich mich ob man die zentrifugalkraft auch zeichnen soll, weil die Lösung zu c) Schwerelosigkeit anscheinend ist? Was ich aber auch nich verstehe weil wie fühlt man sich bitte schwerelos, oder warum? Man ist doch im Kräftegleichgewicht?

Ich kann Aufgabe 4c nicht lösen!Also der Durchmesser ist ja 230(und der Radius 115) und T ist 6600 aber warum ist das verboten?

Ich lerne wirklich ungern auswendig und möchte die Zusammenhänge verstehen.

Die Gravitationskraft und die Zentripetalkraft verstehe ich, aber welche Kraft stellt die Hypothenuse des Kraftdreiecks dar???

Ein Transporthubschrauber hat einen Rotor eines bestimmten Radiuses.

Argumentiere nun anhand der Formeln ohne Rechnung, wie sich diese ändert,​ wenn man einen Punkt in der Mitte des Rotorblattes betrachtet.​

1) Wenn man die Formel a(zp)​=ω^2⋅r benutzt, halbiert sich die Zentripetalbeschleunigung auch, wenn man den Radius halbiert.

2) Wenn man die Formel a(zp)​=v^2/r benutzt, verdoppelt sich die Zentripetalbeschleunigung, wenn man den Radius halbiert.

Rein von der Formel her gesehen, ergibt das für mich Sinn. Aber praktisch nicht so sehr...

Wenn man 1) betrachtet: Wenn sich r halbiert, muss der weiter-innere Punkt ja in derselben Zeit den gleichen Winkel hinter sich bringen, wie der äußere Punkt. Ich stell mir das mit dem Abbiegen eines Autos in einem Kreisverkehr vor, da man dann, wenn der Kreis enger ist, das Lenkrad viel weiter umdrehen muss, also die Richtung viel stärker ändern muss, also eine größere Geschwindigkeitsänderung, also eine stärkere Beschleunigung hat...

Aber nein, die Formel sagt, die Beschleunigung wird halbiert...

Wenn man 2) betrachtet: Wenn sich r halbiert, legt der weiter-innere Punkt ja in derselben Zeit eine viel kürzere Strecke zurück als der äußere Punkt, daher müsste v ja viel langsamer sein...

Aber nein, die Formel sagt, die Beschleunigung wird verdoppelt...

Wieso ich verstehe das einfach nicht T.T

Würde mich sehr über jegliche Antwort freuen, LG Mayu

Wir haben gelernt:

"in der Kreisbewegung ändert sich die Bahngeschwindigkeit ständig, zwar nicht wegen dem Betrag, aber wegen der Richtung. Und wenn eine Änderung der Richtung, also der Geschwindigkeitsvektoren vorliegt, liegt auch eine Beschleunigung vor, daher gibt es die a(zp) (Zentripetalbeschleunigung), mit der man F(zp) berechnet. Aber die Energie ändert sich nicht, weil die Formel lautet

E(kin) = 1/2 * mv^2

und die Geschwindigkeit sich ja nur mit dem Vorzeichen +/- ändert (weil Richtungsänderung), d.h. das Quadrat lässt das Minus verschwinden und die Energie ändert sich nicht. Basta."

So, wenn man diese Logik jetzt aber auch auf die Formel der a(zp) anwenden würde, würde man bei etwas kuriosem rauskommen, da:

a(zp) = v^2/r = ω²*r

Bei beiden Geschwindigkeitsvarianten ist ein Quadrat dabei, d.h. auch hier würde sich das neg. Vorzeichen auflösen. Warum existiert dann aber a(zp), aber nicht eine Änderung der kin.Energie, obwohl man die gleiche Logik anwendet?

Würde mich sehr über eine Erklärung freuen 🥲

LG und vielen Dank fürs Durchlesen,

Mayu, 11.Klasse Bayern

Guten Morgen liebe alle zusammen,

ich habe ein Verständnisproblem was der Unterschied beider im Zusammenhang für Atome ist. Für mich klingt das von der Beschreibung her beides so ähnlich. Und eine weitere Frage von mir wäre, was genau für diese Drehbewegung um den Kern Zuständig ist?

In welcher Situation ist die Gefahr wegzurutschen größer: 1.: ich fahre 45° Schräglage bei sehr niedriger Geschwindigkeit aber sehr engem Kurvenradius oder 2.: ich fahre 45° Schräglage bei hoher Geschwindigkeit und großem Kurvenradius.

Hi Community,

im Physikkurs behandeln wir gerade das Thema Winkelgeschwingigkeit.

Die Winkelgeschwindigkeit w (Omega) wird ja in 1/s oder s^-1 angegeben und mit Bogenmaß/Zeit berechnet, aber warum das. Wären °/s oder Umdrehungen/s nicht sinnvoller?

Warum wird eben in dieser Einheit gerechnet und nicht in den anderen genannten?

Wer Näheres weiß gerne melden.

Mfg

DerEineHalt08

Ich habe eine Frage zur Bahn- und Winkelgeschwindigkeit. Nehmen wir mal an der Radius von einem Hochrad ist 62cm und der des Hinterrads 22cm. Wie ist es möglich, dass beide Räder denselben Bahngeschwindigkeitsbetrag haben? Die Bahngeschwindigkeit ist doch vom Radius abhängig? In der Lösung von meiner Buchaufgabe steht, dass beide dieselbe haben? Wenn, dann haben sie dieselbe Winkelgeschwindigkeit, da beide Räder denselben Winkel im Zeitintervall t überstreichen...Kann mir jemand bitte weiterhelfen?

Hallo Leute, das ist vielleicht eine dumme Frage, aber aus irgendeinem Grund kann ich keine Antwort finden.

Hallo Leute, ich komme bei Aufgabe 2 und 5 nicht weiter. Könnte mir hier bitte jemand helfen?

Kann mir wer helfen hab keinen Plan

Aufgabe:

Alwin fährt auf seinem Skateboard in 5,0 min 900 m weit. Sein Bruder Anton legt mit sei- nem Fahrrad 15 km in einer Stunde zurück. Be- rechnen Sie die Beträge der jeweiligen Durch- schnittsgeschwindigkeiten in m/s.

Hey,

Ich wollte mal schauen, wann welcher Winkel maximal ist. Dafür habe ich 2 Planeten um einen Stern laufen lassen und die jeweiligen Winkel gemessen. Ich habe bemerkt, dass wenn der Winkel bei Q in einem 90 Grad Winkel steht, der Winkel R maximiert ist. Kann mir das jemand mit einer logischen Schlussfolgerung bestätigen?

Dd

Hallo,

um die Kräfte, die im Looping wirken besser zu verstehen, habe ich mir Videos auf YouTube dazu angeguckt. Mindestens die Hälfte der Videos versuchen eine anschauliche Erklärung, warum F(G) =F(Z) im obersten Punkt des Loopings gilt, indem sie schwammig in einem Nebensatz erklären, dass es ganz logisch wäre, dass die Zentrifugalkraft in diesem Moment die Schwerkraft der Kugel vollständig kompensiert.

Ich verstehe nur nicht, wie man da ernsthaft physikalisch-anschaulich mit der Zentrifugalkraft erklären möchte, dass das gilt. Ich ging davon aus, dass die Zentrifugalkraft eine Scheinkraft sei, und nur im System der Kugel relevant wäre, deswegen ist es mir so fremd, dass da locker die Hälfte (und das beschränkt sich nicht nur auf den Fall des Loopings) mit der Zentrifugalkraft kommen.

Mir ist klar, dass die Mathematik die gleiche bleibt, ob nun Zentripetal oder Zentrifugalkraft, nur ich kann mir da einfach keinen Reim draufmachen wie man anschaulich vermitteln möchte, dass die Zentrifugalkraft eine real existierende Kraft sei, die die Kugel nach aussen drückt.

Was für mich immernoch nicht die Frage klärt, wieso im obersten Punkt F(Zentripetalkraft) = F(G) gilt.

Lieg ich im oben ausgeführten falsch?

Danke im Voraus!

Winkelgeschwindigkeit-Definiton

Hallo,

ich habe eine Frage,

die Winkelgeschwindigkeit ist ja beispielsweise durch zurückgelegten Winkel durch Zeit definiert, also:

Ich weiß es hört sich bisschen dumm an, aber nehmen wir an, wir hätten ein Dreieck:

Und der Winkel Alpha Links ist anfangs größer und danach (rechts) wird er kleiner (Im Schaubild geht es um die Umkreisung zweier Planeten um einen Stern). Die Abnahme von Alpha und die benötigte Zeit dafür kann aber nicht für die Winkelgeschwindigkeit verwenden werden (oder), da die Winkelgeschwindigkeit wie oben definiert ist.

Zudem (hat jetzt nichts mit dem Thema zu tun). Wenn ich 5 durch 4 teile, erhalte ich 1,25. Das bedeutet also, 125 Prozent von 4 ist 5, aber wie würde ich das mit „um“ definieren. 5 ist um 25 Prozent größer als 4 (hier kommt es ja drauf an welche 25 Prozent man meint). 

Hallo,

Ich muss eine Aufgabe in Physik lösen und komme aktuell nichtmal auf einen Ansatz

Das ist die Aufgabe und unten befindet sich die Lösung.

Ich würde mich wirklich sehr über einen Tipp freuen und danke im voraus.

(Gelerent haben wir hauptsächlich die zentripetalkraft)

Liebe Grüße

Hallo weiß jemand wie die a, b und c geht, weil ich habe Probleme mit diesen Aufgaben

Was ist die Formel für das Trägheitsmoment eines Zylinder dessen Masse nicht außen wie bei einem Hohlzyliner sondern innen nahe der Drehachse angebracht ist?

Was ist der Zusammenhang zwischen Trägheitsmoment und Winkelgeschwindigkeit? Die Formel für das Trägheitsmoment ist ja I=m x r^2 Wie ist nun der Zusammenhang zu der Winkelgeschwindigkeit? Bei einer Pirouette wird die Drehgeschwindigkeit ja größer mit kleinerem Trägheitsmoment...

Hallo,

ich heiße Paul und verstehe nicht wie schnell ein Satellit sein muss und wie man seine Geschwindigkeit berechnen kann. Was das alles mit der Zentripetalkraft zu tun hat ist mir bekannt. Wahrscheinlich ist es garnicht so schwer aber ich verstehs nicht wenn ich es von meinem Lehrer erklärt bekomme.

Ich würde mich sehr über eine Antwort freuen.
Vielen Dank im voraus

LG Paul

Die Zentrifugalkraft kann ich mir super vorstellen. Wenn ich in meinem Flugzeug sitze und eine enge Kurve fliege, spüre ich eine Kraft, welche mich in den Sitz drückt und stärker wird, desto schneller ich bin / desto enger die Kurve ist.

Nun fällt es mir etwas schwerer mit der Zentripetalkraft. Diese verstehe ich leider nicht. In einem Riesenrad soll diese Kraft direkt in die Rotationsachse hineingehen. Aber diese Kraft spüre ich nicht. Ist sie gleich der Zentrifugalkraft, weswegen diese sich herauskürzt? Wie kann ich sie mir besser vorstellen und wieso kürzen sich diese Kräfte nicht im Flugzeug aus, wenn ich eine Kurve fliege?

Müssen nur Aufgabe b und c machen aber für mich ergeben die Aufgaben keinen sinn, danke schonmal für antworten

Erfolgt eine Kreisbewegung beider personen mit gleicher winkelgeschwindigkeit wenn sie mit konstanter geschwindigkeit im karussel innen und außen sitzen

Haben Aufgaben in Physik, verstehen sie nicht und brauchen hilfe, bitte :D

Wir Berechnen die Zentripetalbeschleunigung absolut und im Vergleich zur Erdbeschleunigung g=9,81m/s²

a) einer Astronautentestmaschine (Abstand Drehachse Kabine 6,5m, 20U/min)

b) auf der Erde am Äquator bzw. auf 45° Breite infolge der Drehung der Erde um ihre Achse

Danke schonmal

Stehe gerade irgendwie komplett auf dem Schlauch, kann mir wer helfen?

Bahngeschwindigkeit v

Umlaufdauer T

Drehfrequenz f

Winkelgeschwindigkeit w

Hi, wir sollen für den Physikunterricht berechnen, wie schnell ein 600kg schweres Auto mit 700N in eine Kurve mit dem Radius r=200m fahren darf. Und ich weiß nicht so ganz wie. Ich hab gedacht mit E=m×c² irgendwie?

LG, danke im vorraus

Der Stundenzeiger einer Turmuhr (Länge des Zeigers = 1,25 m) ist fest mit einem Zahnrad (z = 96 Zähne) verbunden. Dieses wird von einem Zahnrad Z2 mit 32 Zähnen angetrieben.

Welche mittlere Winkelgeschwindigkeit hat Z2?

Das Ergebnis ist 0,025 °/s
Die Rechnung wäre: ( 2* 360° / 24h * 60min * 60s ) * 3
Aber warum rechnet man nicht mit 2*Pi*360° ?

Das ist die Aufgabe. Ich habe sie meines Erachtens richtig gelöst. Was bekommt ihr als Ergebnis heraus?

Ein Stück Eis gleitet reibungslos eine schiefe Ebene mit einem Winkel von 50° zur horizontalen hinunter und rutscht in einen kreisförmigen Looping hinein. Eine experimentelle Auswertung des Versuches hat ergeben, dass das Stück Eis bei der halben Höhe im Looping noch eine Geschwindigkeit von 8 m/s besitzt und die Kreisbahn bei einem Winkel von 60° (zur Horizontalen) aufgrund einer zu geringen Bahngeschwindigkeit verlässt.

Berechnen Sie die Höhe des Loopings aus dem Versuch.

Ein Fahrzeug (=0,25kg) durchfährt eine loopingbahn (d=30 cm) mit der Geschwindigkeit 4,0 m pro Sekunde. Wie groß ist die Kraft die das Fahrzeug im höchsten Punkt auf die Bahn ausübt und mit welcher mindestgeschwindigkeit muss das Fahrzeug durch den höchsten Punkt fahren damit es nicht runterfällt?

In der Aufgabe rollt eine Kugel eine schiefe Ebene hinab, und man soll die Endgeschwindgkeit bestimmen. Mein Ansatz siehe Bild. In der darauffolgenden Teilaufgabe heißt es dann, welchen Radius müsste ein Vollzylinder haben, damit er die gleiche Geschwindigkeit erreicht. Nun ist das Trägheitsmoment eines Vollzylinders 0.5 * m * r^2 . Dadurch kürzt sich in der Gleichung aber wieder der Radius heraus. Was mache ich falsch oder hängt die Geschwindigkeit nicht vom Radius hab?

Eine Person sitzt auf einem sich mit konstanter Geschwindigkeit drehenden Karussell.

Eine Verdopplung der Winkelgeschwindigkeit führt zu einer Verdopplung (i) der Frequenz; (ii) des Betrags der Bahngeschwindigkeit; (iii) der Umlaufzeit; (iv) des Betrags der Zentripetalbeschleunigung.

Das is ne Aufgabe von ner Uni.

Ein Eisklotz gleitet reibungsfrei eine schiefe Ebene hinunter und durchläuft einen Looping. Es sind die Höhe der Abfahrt und der Radius des Loopings gegeben. Verluste sollen vernachlässigt werden.

Gesucht ist nun eine Funktion, die die G-Kraft (Vielfaches von g) in Abhängigkeit der Höhe (gerade nach oben vom tiefsten Punkt) im Looping beschreibt.

Ich meine so eine Art Karte, wo man sieht welche Größe von was abhängt und wie sie zusammenspielen.

Zb für Sachverhalte wie: Ein Eisklotz gleitet reibungsfrei eine schiefe Ebene hinunter und durchläuft einen Looping. Es sind die Höhe der Abfahrt und der Radius des Loopings gegeben. Verluste sollen vernachlässigt werden.

Gesucht ist nun eine Funktion, die die G-Kraft (Vielfaches von g) in Abhängigkeit der Höhe (gerade nach oben vom tiefsten Punkt) im Looping beschreibt.

Sind die Bahnen so gebaut, dass man oben am Looping schwerelos ist oder ist die Zentrifugalkraft noch vorhanden, sprich man wird in den Sitz gedrückt?

Wie könnte ich die Aufgabe beantworten?
Wäre super wenn ihr mir helfen könntet 😅

Ein Auto durchfährt eine ebene Kurve mit dem Radius r = 40m. Die Haftreibungszahl ist Mü = 0,6.

Wie und was rechne ich?

Bei der aufgabe f ging es um das experiment fadenstrahlrohr . Mein lehrer hat mir nicht die volle punktzahl gegeben da ich nicht angegeben habe, das man die richtung des elektronenstrahl ändern kann damit der radius gleichbleibt. Ich wiederum glaube das wenn man nur die richtung des magnetfeldes umkehrt der radius trotzdem gleichbleibt nur die kreisbahn sich verändert. Kann mir wer dabei helfen?

Hallo, ich studier Physik im 1. Semester und bin zu blöd für die Aufgabe, kann mir jemand helfen?

Ein Teilchen der Masse m ist mit einem masselosen Faden verbun- den, der durch ein Loch in der Tischplatte geführt wird. Wenn der Faden von der Hand unter dem Tisch festgehalten wird, läuft das Teil- chen auf einer Bahn mit dem Radius r1 und Geschwindigkeit v1. Wird die Hand abgesenkt, ändert sich die Bahn zu r2 und v2.

a. Wie hängt die Endgeschwindigkeit v2 des Teilchens von r2 ab?

b. Welche Arbeit W muss aufgebracht werden, um das Teilchen von der Bahn mit r1, v1 auf eine

Bahn mit r2, v2 zu ziehen? Berechnen Sie dazu das entsprechende Wegintegral.

c. Wie unterscheiden sich die kinetischen Energien der beiden Bahnen? Vergleichen Sie das Er- gebnis mit der in Teil b. berechneten Arbeit W .

Soll man hierfür die Formel az=v^2/r rechnen? Wenn ja was wäre az?

Hallo,

ich komme bei den Teilaufgaben 1b und d nicht weiter..

Kann mir hier jemand helfen?

Beim Mond und Satelliten gilt ja, dass die Gravitationskraft und Zentripetalkraft gleich groß sind, weil sie sich auf einer Kreisbahn um die Erdachse bewegen. Wieso ist die Gravitationskraft und Zentripetalkraft beim Menschen aber nicht gleich groß, obwohl wir uns auch auf einer Kreisbahn um die Erdachse bewegen?

Wirkt auf den Menschen die Zentripetalkraft oder rotieren wir uns um die Erdachse aufgrund der Trägheit der Erde?

Der Big Ben ist eines der bekanntesten Wahrzeichen von London und seine Uhr zeichnet sich durch ihre beeindruckenden Zeiger aus. Der Minutenzeiger des Big Ben hat eine La ̈nge von 4.2 m und der Stunden- zeiger hat eine La ̈nge von 2.7 m.

a)Berechnen Sie die Winkelgeschwindigkeit ω des Minuten- und Stundenzeigers in Radiant pro Sekunde.

b) Wie groß ist der Betrag der Geschwindigkeiten, mit denen sich die Zeiger an ihren Spitzen drehen?

Als ich noch sportlich unterwegs war, bin ich gerne Sprintstrecken gelaufen. Besonders die 200m. Es machte mir Spaß so volle Brezel auf der Innenbahn in Schräglage durch die Kurve zu heizen. Nun zur Frage. Nehme wir an, dass die Kurve durch Sägezahnwellen-Geradenstücke angenähert wird, dann laufen wir ein Stück auf einer Tangente und müssen anschließend, z.B. durch eine Radialbewegung, auf eine Kreisbahn zurück. Das Rücksetzen auf die Kreisbahn ist mit einer Beschleunigung verbunden. Also auch mit einer Kraft und damit mit e8ner Arbeit.

Frage 1: erfordert der Kurvenlauf eine Zusätzliche Arbeit?

Frage 2: Schubse ich auf eine kreisförmigen Kugelbahn eine Kugel an und setze Reibungsfreiheit voraus, wird die Kugel langsamer, weil sie ja auch „immer auf die Kreisbahn zurückgeholt“ werden muß?

mit Hilfe dieser Formel:

Danke vielmals

Guten Abend,

woher weiß man hier bei b), dass der Haftreibungskoeffizient hier mindestens den Wert 0,68 haben muss? Bezieht sich das auf die Formel der maximalen Haftreibungskraft Fhr,max = Haftreibungszahl * Fn? Bedeutet das, dass in dieser Aufgabe die Gewichtskraft die Normalkraft ist? Ist meine Vermutung richtig? In welchen Fällen ist die Gewichtskraft gleich die Normalkraft und in welchen Fällen ist die Gewichtskraft ungleich der Normalkraft?

[AUFGABE]

[LÖSUNG DER AUFGABE]

[MEINE BERECHNUNGEN ZUR AUFGABE]

[FORMELSAMMLUNG]

Guten Abend,

ist meine Rechnung hier falsch? Ich habe Werte von der vorherigen Aufgabe genommen, um auf die Lösung zu kommen (für die Masse M der Erde und den Radius r der Erde).
So war die Aufgabe 6 vermutlich nicht gedacht.

Ich freue mich über eure Hilfe.

Aufgabe:

Lösung zur Aufgabe 6

Meine Berechnungen zur Aufgabe 6:

Guten Abend,

• ist meine bearbeitete Aufgabe a) falsch?
• Die Haftreibungskraft Fhr und die Gewichtskraft Fg gleichen sich doch aus, wenn der abgebildete Fahrgast an die Innenwand des Zylinders gepresst wird und nicht herunterrutscht. Dann wirkt doch auch nur die Zentripetalkraft Fzp auf den abgebildeten Fahrgast.
• In der Lösung steht jedoch, dass auf den abgebildeten Fahrgast die Gewichtskraft Fg, die Haftreibungskraft Fhr und die Unterlagenkraft wirken. Ist das so richtig?

Wichtige zusätzliche Frage: Ist die Unterlagenkraft hier das gleiche wie die Zentripetalkraft Fzp, also nur eine andere Bezeichnung?

Aufgabe:

Lösung zur Aufgabe:

Meine bearbeitete Aufgabe a):

Guten Abend,

leider verstehe ich die Aufgabe noch nicht so wirklich… Wieso sind hier in der Lösung zwei Kreise eingezeichnet? Der Radius der Kreisbahn (Teilaufgabe a)) müsste doch von dem Massenschwerpunkt der Kugel bis zum Massenschwerpunkt des Menschen sein. Wieso ist dann der Radius der Kreisbahn nicht 1,8 m, sondern 1,7 m?

Ein GRACE Satellit zur Untersuchung des Graviationsfelds der Erde besaß eine Masse von 490kg. Er umrundete die Erde auf einer Kreisähnlichen Bahn in einer Höhe von 500km über der Erdoberfläche.

a. Berechnen Sie die Energie, die mindestens Notwendig war, um ihn auf seine Umlaufbahn zu bringen.

b. Berechnen Sie seine Bahngeschwindigkeit.

Könnte man mir helfen um auf Lösungsansätze zu kommen wie zum Beispiel mir die Schritte zu nennen oder die jeweiligen Formeln. Die ganze Lösung muss man mir nicht senden und ich weiß das ich lange dauern würde.

Ja. Also warum ist die Gravitationskraft in dem Fall die Zentripetalkraft

Wieso setzt er hier FZ = FG bei a) und wieso ist omega = v * r und Omega = 2pi/T, also wieso kann man die gleichzeitig anwenden?

Wieso reicht es wenn die Winkelgeschwindigkeit gleich groß ist und wieso ist r automatisch der Abstand des erdmittelpunktes vom Satelliten?

Quelle: https://www.youtube.com/watch?v=NKwjgMus2Jg&t=426s

Eine Frage in Physik?? Ich brauche eure Hilfe!!!!

Danke

Hilfe

Ich brauche eure Unterstützung bei dieser Physikaufgabe

Eine PKW mit Vorderradantrieb hat eine Masse von 1,546 t und einen Radabstand von 2,71 m. Sein Schwerpunkt liegt ca. 0,6 m über dem Boden und 1,2 m vor der Hinterachse.

Berechne für eine Haftreibungszahl von 0,6 die maximal mögliche Beschleunigen?

Was soll man da genau berechnen? Okay, wenn man T weiß, muss der Satellit dasselbe T haben, aber schneller fliegen. Und inwiefern soll man da jetzt den Radius der Umlaufbahn bestimmen? Ich meine, das kommt doch ganz drauf an, wie schnell der Satellit fliegt, also entweder er fliegt langsamer und schafft die Rotation nur mit geringerem Radius, oder fliegt schneller und schafft die Rotation mit größerem Radius. Aber was, wenn keine Geschwindigkeit gegeben ist? Der Radius kann dann doch alles mögliche sein, oder nicht?

Was ist da der Unterschied?

Warum ist bei der Zentripetalkraft die winkelgeschwindigkeit^2 mal r gleich die bahngeschwindgkeit^2 durch r ?

Hallo,

ich habe eine Übungsaufgaben (keine Hausaufgabe o.ä.) für eine anstehende Klausur und stehe da komplett auf dem Schlauch. Selbst mit Formeln blicke ich nicht wirklich durch. Könnte mir jemand helfen?

Vorgegeben ist:

1) Rotordurchmesser eines Hubschraubers ist 10m

2) er dreht sich im Flug 420 Mal pro Minute um die eigene Achse

Aufgaben: Jetzt soll die Frequenz, Winkelgeschwindigkeit und die Umlaufdauer berechnet werden. Außerdem die Zentripetalbeschleunigung und Bahngeschwindigkeit für den Punkt an der Spitze eines der 4 Rotoren

Im Formelbuch habe ich folgendes gefunden:

Frequenz ->f = 1HZ = 1/s aber was soll ich damit anfangen?

Winkelgeschwindigkeit muss ich wahrscheinlich die Formel die angekreuzt ist nehmen, weil es ja nicht konstant beschleunigt wird oder?
Muss ich dann 2 x Pi x 420 rechnen?

Zu Umlaufdauer finde ich nur was mit siderischer Umlaufzeit aber das ist doch nicht richtig oder? Ich muss doch was mit T = …. haben. Formt man da eine andere Formel nach T um?

Zur Zentripetalbeschleunigung steht das

Welche Formel nimmt man dann für die Bahngeschwindigkeit?

Für Hilfe wäre ich sehr dankbar

Hallo! Leider hab ich bei der Einführung des Themas gefehlt und verstehe nicht wie ich folgende Aufgaben lösen kann :/

1.) Ein gleichförmig kreisender Ball führt in t = 10 s genau 30 Umläufe auf einem Kreis mit dem Radius r = 0,6 m aus. Wie groß sind die Drehfrequenz f, die Umlaufdauer T, die Winkelgeschwindigkeit  und die Geschwindigkeit v des Balls?

2.) Mit welcher Geschwindigkeit können Späne von Werkzeugschleifmaschinen (r = 10 cm) wegfliegen, wenn die Scheiben 2800 mal in der Minute rotieren?

3.) Punkte an der Oberfläche eines kugelförmigen Kopfes (Durchmesser 1 mm) eines Zahnbohrers können eine Geschwindigkeit von 75 km/h erreichen. Wie groß ist dann die Umdrehungszahl pro Minute des Bohrkopfes, Wie groß ist die Winkelgeschwindigkeit?

danke I’m Voraus!

Hallo,

ich habe eine Aufgabe in Physik gelöst, nur habe ich leider keine Lösung dazu.

die Aufgabe ist:

Der Mondlandeanzug von Neil Armstrong hatte auf der Erde eine Gewichtskraft von 820N.

Welche Masse & Gewichtskraft hatte es auf dem Mond?

Rechnung: 820N=9,81 * m

m= 83,59 Kg

Fg Mond= 1,6 * 83,59kg

= 133,74N

Antwort: Die Masse auf dem Mond war 83,59Kg und die Gewichtskraft 133,74 N.

ist das richtig so? Ich habe demnächst eine Prüfung.

Danke im Voraus.

Welchen Durchmesser hat eine Kreisscheibe von 8kg Masse deren Trägheitsmoment 1,69kg*m^2 beträgt?

habe das mit der formel J=m*r^2 berechnet, bekomme aber für d=0,92m raus, aber in den lösung steht 1,3m was ist falsch?

Hallo,

ich habe folgende Aufgabe berechnet:

Ein Bob durchfährt eine Kurve mit dem Radius 25m mit einer Geschwindigkeit von 108 km/h. Der Bob nutzt dabei die Kurvenüberhöhung der Bobbahn aus. Wie groß ist der Neigungswinkel φ bei der gegebenen Geschwindigkeit?

ich habe bereits in die Lösung geschaut und habe gesehen, dass ich alles richtig gemacht habe (also tan (φ ) = 3,67). Nur habe ich das Problem, dass wenn ich im Taschenrechner arctan(3,67) den Winkel nicht herausbekomme, sondern 1,3 , was in dieser Aufgabe nicht funktioniert. Jedoch MUSS der Neigungswinkel so berechnet werden.

Liegt es an mir oder am Taschenrechner?

Vielen dank im Voraus :).

Ich habe eine kurze Frage zu der Kraft Fz… was passiert wenn diese beim Beispiel vom Kettenkarussell nicht da wäre? Würden die Sitze trotzdem so weit nach außen „gezogen“ werden? Oder würden sie nur von der Gewichtskraft nach unten gezogen werden?

Hallo, ich verzweifle gerade ein bisschen, ist wahrscheinlich gar nicht so schwer, wie berechne ich T wenn ich den Radius (28cm) und die Geschwindigkeit des Autos (100km/h) habe?

Folgende Aufgabe:

Aus der Gleichung F = m v^2 / r folgt, dass F antiproportional zu r ist; nach der Gleichung F = m ω^2 r sind sie aber proportional zueinander. Erklären Sie dies.

Mein Ansatz ist, den Zusammenhang zwischen v und ω zu nutzen: ω = v / r. ω ist also antiproportional zu r. Die eigentlich hergeleitete Formel für die Zentripetalkraft ist F = m v^2 / r. Da hier mit r dividiert wird, muss, wenn man ω statt v verwendet mit r multipliziert werden, da die beiden Größen antiproportional zueinander sind.

Ist diese Begründung richtig, ich bin selber nicht ganz überzeugt davon…

Dankeschön im Voraus!

Ein Elektromotor hat eine Drehzahl von 200 Hertz. Berechne seine Umlaufdauer seine Winkelgeschwindigkeit und die Anzahl der Umdrehungen pro Minute.

Das ist die Aufgabe, ich verstehe nicht wie ich ohne jegliche Angabe es berechnen soll.

Könnte mir jemand, die c) erklären? :)

Danke im Voraus

Ein Auto der Masse 𝑚1 = 10 kg liegt auf einem schrägen Dach (schiefe Ebene) und sei über ein leichtes Seil mit einem Massestück 𝑚2= 4 𝑘𝑔 verbunden.

Der Neigungswinkel des Daches ist 𝛼 = 40°.

Wie groß muss die Haftreibungszahl 𝜇𝑅,ℎ mindestens sein, damit das Auto ruht?

Hallo könnte jemand mir bitte mit Frage c helfen ?

1. Ein Radfahrer (Masse einschl. Fahr-rad: 80 kg) fährt mit 36 km/h in eine enge Kurve (mit einem Radius von 30 m). Da die Fahrbahn sandig ist, beträgt die Haftreibungszahl hat = 0,3. Schafft der Radfahrer die Kurve?

Ich verzweifle wirklich an dieser Aufgabe, würde mich über eine Antwort freuen,da ich ein Ergebnis habe und wenn dies falsch ist den richtigen Weg hätte.
gegeben: Umfang Erde: 40.000 km
Umlauffrequenz 24 Stunden
Masse Person 70kg

gesucht: Gewichtskraft am Äquator und am Nordpol

Danke im Voraus!!!

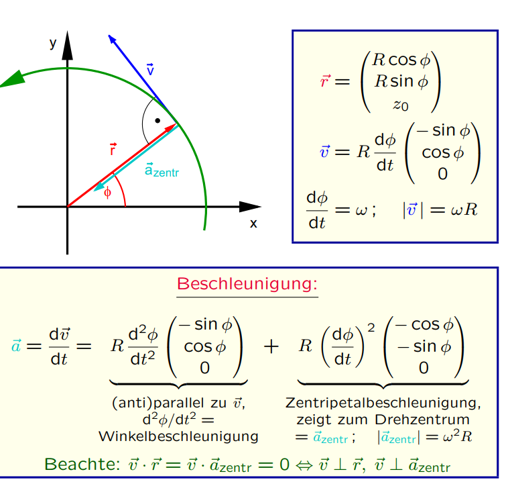
Gerade habe ich fast alles zu Kreisbewegungen verstanden und bin jetzt dabei, das letzte Rätsel diesbezüglich zu knacken, und zwar die Beschleunigung.

Was ich eigentlich immer dachte, war, dass die Beschleunigung die 2. Ableitung von r ist. Ich meine, der Vektor von v ist ja auch die Ableitung von r.

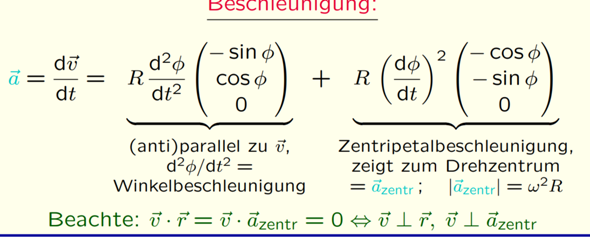
Dementsprechend dachte ich, dass der Vektor von der Zentripetalbeschleunigung die 2. Ableitung von r ist, weil das von dem Vektorinhalt so passt, aber anscheinend steht davor nicht 2. zeitliche Ableitung von phi, sondern was anderes, deshalb fällt das schon mal weg?

Ist es stattdessen richtig, dass der eine Vektor von a antiparallel zu r ist, und der andere (anti)parallel zu v? Dann würde das, was im Vektor steht, schonmal Sinn machen.

Und das Zeug davor? Wenn die Vektoren einfach nur die (anti)parallele Version von einem anderen Vektor sind, hat das auch nichts mit Ableitung zu tun, oder? Heißt das, das Zeug vor den Beschleunigungsvektoren hat z.B. nichts mit der Kettenregel einer Ableitung zu tun, im Gegendatz zu dem Zeug vor V?

Oder sind die Vektoren doch Ableitungen von irgendwas? Wenn ja, ich dachte, a ist immer 2. Ableitung von r, wieso sind das dann unterschiedliche Vektoren?

Oder geht es bei dem Zeug davor einfach nur darum, wie lang der Vektor ist?

Also bei dem 2. dann w^2r, weil das die Länge eines normalen Beschleunigungsvektors ist, oder?

Und bei dem 1. Teil die Winkelbeschleunigung. In dem Fall hat dann R nichts mit der Beschleunigungsformel zu tun, weil die Winkelbeschleunigung nur d^2phi/dt^2 ist?

Also besteht die Gesamtbeschleunigung aus 2 Teilen, dabei geben die Vektoren die Richtung an und der Teil davor jeweils die Länge?

Oder hat das doch was mit Ableitung von v oder r zu tun?

Entschuldigt die lange Frage, ich hoffe, man konnte sie verstehen.

Und aus Interesse, Wieso ist da nur ein Vektor a aufgezeichnet?

Es wird ja zwei mal "2. zeitliche Ableitung von phi" gesagt. Allerdings ist das einmal (d^2phi/dt^2) und einmal (dphi/dt)^2. Hat das was zu bedeuten, dass es zwei unterschiedliche Schreibweisen gibt?

Es geht um die Kreisbewegung in der Physik und dass v die Ableitung von r (Ortsvektor) ist. Mit der Kettenregel ist die innere ableitung bei der x und y Koordinate ja dphi/dt. Aber nur bei x und y, z hat ja nur z0. Wieso wird dann aber die innere Ableitung ganz vor den Vektor geschrieben, obwohl das nicht auf alle Koordinaten zutrifft? Oder ist es so, weil es egal ist und es wegen z(v)=0 keinen Unterschied machen würde?

Ich weiß wie man die Geschwindigkeit im höchsten Punkt berechnet, sodass man nicht raus fällt aber wie berechnet man sie im tiefsten Punkt?

Schon mal danke im Voraus!

Warum fliegen die stehenden Fahrgäste eines Buses bei scharfem anfahren aus dem Stand nach hinten?

Hallo, könnte mir vielleicht jemand helfen? :)

„Für Spielzeugautos gibt es Loopingbahnen, bei denen die Autos auf einer biegsamen Anlaufbahn beschleunigt werden. Der Looping der Bahn habe einen Durchmesser von 25cm. Berechnen sie die Höhe, aus der das Auto mindestens starten muss um den Looping durchfahren zu können.“

Danke schonmal im vorraus!

Meine Frage:

Hey I am sry dass ich momentan so viele Fragen stelle, aber Übung macht ja bekanntlich den Meister (hoffentlich haha)

Also folgende Aufgabe: ein Karussell auf dem Spielplatz mit dem Trägheitsmoment Ik und Radius R drehe sich ohne Reibung mit der Winkelgeschwindigkeit w. w=20 1/s, Ik=50Kgm^2, R=1,50m

a) Nun lässt ein Kind Sand auf den Rand des Karussels rieseln mit der Rate dm/dt= 50g Berechne die Änderung der Winkelgeschwindigkeit delta W nach einer Minute. Nehme an, dass der Sand Kreissymetrisch am äußeren Rand des Karussells verteilt ist.

b)Das Kind (m=25Kg) springt tangential gegen die Drehung des Karussells mit v=1m/s relativ zum Boden auf den Rand des Karussells. Berechne wieder die Änderung der Winkelgeschwindigkeit. Auch hier gilt w=20 1/s

Meine Ideen:

a) Ich würde hier mit dem Drehimpulserhaltungssatz arbeiten. wobei sich ja das Trägheitsmoment des Karussells ändert, da ja der Sand drauf fließt. Also wäre das Trägheitsmoment mit dem Sand drauf: Ik´=Ik+m*R^2 (m ist nach einer Minute 3Kg ----> 50g*60s)

Ik*w1=Ik´*W2

w2=Ik*w1/Ik´

deltaW= w1-w2

b)Auch hier würde ich wieder mit dem Erhaltungssatz arbeiten

R*m*v= Ik+Ikind*w2

und das wieder umstellen nach w2

stimmt das iwie? oder bin ich mal wieder komplett falsch abgebogen?

aber wie berechne ich das trägheitsmomenr des kindes?

Hallo Community,

Habe heute in Physik folgende Frage bekommen:

Welche Kraft wirkt im Faden eines Fadenpendels, wenn die Kugel den untersten Punkt der Schwingung passiert. Ich schrieb natürlich zunächst ganz klar:

0, weil F(r)~y und hier keine Auslenkung stattfand. Dann war ich mir aber unsicher. Wirkt im Faden (dieser sei masselos) nicht aber auch die Gewichtskraft des Massestücks, welches den Faden leicht dehnt?

Welche Geschwindigkeit muss ein

Wagen im höchsten Punkt B einer Spiel-

zeugloopingbahn (m) Beispiel; r= 15 cm)

mindestens haben, damit er auf der Bahn bleibt?

b) Wie schnell ist er dann im tiefs—

ten Punkt C. Welche Kraft übt er dort auf

die Bahn aus (m = 100 g)?

c) Aus welcher Höhe h muss der Wagen mindestens losfahren

, um sicher den Kreis zu durchlaufen?

Könnte mir jemand da helfen?? :/

Ich verstehs nicht? Sie sind doch genau das Gegenteil von einander. Die eine wirkt nach innen und die andere nach außen

Guten Tag!
Ich habe mich letztens mit der Bahngeschwindigkeit beschäftigt und mich gefragt, wieso es zwei Formeln gibt. v=s/t und v=(2*π*r) / T
Welche Formel sollte ich für folgende Aufgabe benutzen?
Berechne die Bahngeschwindigkeit eines Satelliten, welcher eine Strecke von 480 000 Kilometern auf seiner Bahn innerhalb von 5 Stunden zurückgelegt hat.

Der Sitzende hat bei doppeltem Radius die doppelte Haftkraft.

Die maximale Haftkraft ist überall gleich gross.

Ich komme bei dieser Aufgabe nicht weiter. Vielleicht kann mir jemand helfen?

Ein Auto fährt mit einer Geschwindigkeit von 36km/h über eine Klimagerät. Die Wasseroberfläche befindet sich 10m tiefer. Der Luftwiderstand ist zu vernachlässigen. Das Auto ist als Massepunkt zu betrachten.

a) Berechne, in welcher Entfernung von der Klimagerät das Auto ins Wasser eintaucht.

b) Gib die Bahngeschwindigkeit und die Geschwindigkeit v1 (in x Richtung) v2 (in y Richtung) zu diesem Zeitpunkt (Eintauchen) an.

Hey, ich komme bei der folgenden Aufgabe nicht weiter. Genauer gesagt bei Aufgabenteil b). Mein Ansatz war, über die Hubarbeit zu gehen, allerdings habe ich keine Masse gegeben und weiß nicht, wie ich die Aufgabe anders lösen soll.

Bei c) hätte ich geschätzt, dass das Drehmoment am höchsten Punkt maximal ist, weiß allerdings nicht, wie uch die Formel angeben muss.

Danke schonmal für die Hilfe,

Liebe Grüße, Paul

Ein Ritzel rollt zwischen 2 Zahnstangen. Die obere mit 2 m/s nach links, die untere mit 4 m/s nach rechts. Durchmesser des Ritzel sind 0,3m

Gesucht ist die Winkelgeschwindigkeit des Ritzel und die Geschwindigkeit des Mittelpunktes.

Ansatz. Die Geschwindigkeiten addieren sich zu 6 m/s und über w=v/r kommt man auf 40 1/s, Lösung sind aber 20 Rad/s. Wo ist mein Fehler?

Hallo

es ist eine komische Frage, die sich etwas ähnelt mit einer Frage die ich mal gestellt habe. Weiß jemand aus Erfahrung oder kann vielleicht sogar schätzen, wie schnell eine Mausefalle sich schließt (in m/s bevorzugt geht aber auch in rad/s)? Und wie könnte man ausrechnen wie die geschwindigkeit bei verschiedenen Radien der Mausefalle ist (also sagen wir mal die Mausefalle hat ein Radius r=4,5cm und wenn ich schätzen müsste bewegt sie sich 1410m/s 🤷‍♂️, könnte ich dann die Geschwindigkeit für r=8cm ausrechnen)?

Danke im Vorraus!