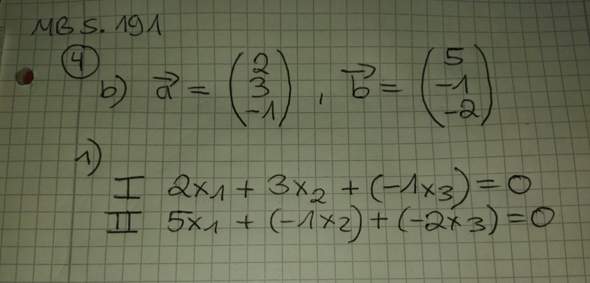in der Schule haben wir besprochen, dass, wenn die Vektoren linear abhängig sind, gilt: (Vektor 1)= r*(Vektor 2) +s*(Vektor 3)
weil ich das Thema aber nicht so sehr verstehe, habe ich auch danach gegoogelt, und da steht plötzlich überall stattdessen
R*(Vektor 1)+s*(Vektor 2)+t*(Vektor 3)=0
also wir machen das auch mit den linearen Gleichungssystemen aus 3 Gleichungen, allerdings immer mit der oberen Formel, und von der unteren hatte ich noch nie was gehört.
-Wie ist das denn jetzt, bzw welche Formel ist richtig? :(
-Also generell verstehe ich auch nicht richtig den Unterschied, was eine Linearkombination ist, und was Linear abhängig? :O
Zur Info, gauß-algorithmus hatten wir auch nicht.
Und noch mal zur Formel, damit berechnet man ja, ob die Vektoren linear unabhängig oder abhängig sind.
-Aber wie ist das z.b., wenn nur zwei davon linear abhängig sind, weil da ja manchmal z.b. steht " zeichnen Sie die Repräsentanten Dreier Vektoren, von denen zwei linear unabhängig, alle drei aber linear abhängig sind"? Gibt es da wohl Unterschiede, das es bei allen Vektoren anders ist als bei einzelnen??
Sorry für diese sehr lange Frage, hatte in diesem Thema von vorneherein Schwierigkeiten, und versuche gerade, alles durchzugehen und es so gut wie möglich zu verstehen, was aber irgendwie nicht gerade gelingt.
Zur Info, die grundlegenden Fragen sind mit einem Bindestrich Markiert. Bin dankbar um jede Antwort! :D