Hey,

ich verstehe nicht wie ich G-Parität auf einen Meson-Zustand wirken lassen soll. Ich verstehe nicht wie das ganze mathematisch funktioniert. Also als Beispiel:

Wie kommt man hier darauf, dass Pi+ negative G-parität hat ?

Was ist Supersymmetrie?

Bzw. ist die Zahl 5 in der Struktur des Kosmos eine wichtige Zahl?

Hey ihr lieben, iwie bin ich absolut verzweifelt. Ich bekomme es einfach nicht hin das Kurvenintegral zu berechnen. Iwie weiß ich, das 7ch das ganze in 4 Teil integral aufteilen muss, da ja ein Rechteck sozusagen vier Wege hat.

Ich weiß ach dass ich iwie den Weg parametrisieren muss, hab aber absolut keine Ahnung wie ich das machen soll :(

Generell bin ich ein bisschen überforderten

Hat wer Erfahrungen gemacht mit mündliche Prüfung in Theoretischen Physik (am besten für den ersten Semester)? Wenn ja, wie ist es für euch gewesen?

Weil ich überlege eine mündliche Prüfung in Theoretische Physik zu machen allerdings haben wir im ersten Semester nur mathematische Grundlagen und weiß daher nicht wirklich wie man nur diese mathematische grundlagen präsentieren soll.

Ich kenn das von Abi so das ich in der Regel nur theoretische Konzepte erklären musste. Als ich z.B. für Abi eine Physik Mündliche Prüfung gemacht habe musste ich halt nur sowas erklären wie ein elektrisches Feld, charakterische röngtenstrahlung etc funktioniert. Ich musste zwar erklären was die Formeln bedeutet haben, aber musste nichts richtiges rechnen.

Denn im ersten Semester für das Physik Studium wird bei theoretische Physik wenig physikalisches Kontext gemacht sonder nur Mathe ...

Ich habe auch mit meinem Prof besprochen das wir am die prüfung so macht das man am Anfang ca. 30 min bearbeitungszeit hat und 20 min Zeit die Aufgaben zu präsentieren. Aber mehr auch nicht.

Hey ihr lieben, ich habe so meine Schwierigkeiten mit dem kronecher und dem Levi cevita Symbol.

Iwie verstehe ich nicht, was genau da passiert ist. Also warum taucht da plötzlich ein kronecker Symbol auf und verschwindet dann wieder, warum werden die Indizes vertauscht, warum wird dann plötzlich transportiert, und warum kommt dann wieder ein kronecker? Ihr seht ich bin absolut list, würde aber so gerne mit den Symbolen umgehen können, daher wäre ich dankbar wenn sich jmd die Zeit für mich nehmen könnte und es mir erklärt.:)

Es gibt doch die beiden Feldstärken E (elektrische) und H (magnetische) und die beiden zugehörigen Flussdichten D (elektrische) und B (magnetische), die auch jeweils die Materialabhängigkeiten (ϵ und μ) berücksichtigen:



(vektorielle Größen)

Nun Frage ich mich jedoch, warum in der historischen "Grundform" der Maxwell Gleichungen meist E und B verwendet werden und nicht die beiden Feldstärken E und H oder die beiden Flussdichten D und B, die dann auch in Materie gelten.
Stattdessen nutzt man die elektrische Feldstärke, aber die magnetische Flussdichte.

Mir ist bewusst, dass man dies auch durch Einsetzen und Unformen erreichen kann, aber in fast jeder Fachliteratur findet man die "historisch entstandene" Kombination, wie es dort oft heißt.

Auch wenn man über elektromagnetische Wellen spricht, nutzt man zur Beschreibung fast immer E und B. "E und B stehen senkrecht aufeinander und senkrecht zur Ausbreitungsrichtung".

Wenn jemand eine tiefgreifende Erklärung hat (ich habe schon oft schwammig gehört "liegt an der historischen Entdeckung...", würde ich mich über eine ausführliche Antwort freuen.

Jemand sagte mir einst, sie sei eine "superkritische Flüssigkeit" oder so ähnlich.

Hey in der VL haben wir über die Streuwinkel gemittelt

Iwie verstehe ich nicht wie man auf diese Integrale kommt und woher man die Grenzen hat. Woher kommen da plötzlich überall die pies her? Verstehe auch nicht genau wie die Substitution durchgeführt wurde

Also T steht für Kin Energie. Wir haben iwie die Masse Am definiert, wobei ich nicht ganz verstehe was genau das A jetzt eig bedeutet

Wußtet ihr, daß Hühnerküken einen Bauchnabel haben?
Tja, was ich nicht weiß ist die Lösung folgender Aufgae

Einen Ansatz muss ich natürlich auch liefern, das ist ja klar

i) Also ich hätte jetzt einfach die partiellen Ableitung nach x,y und z gebildet.

dV/dx = y² + z² 3²

dV/dy = 2yx + e^(-yz) (-z)

dV/dz = 2zx³ + e^(-yz) (-y)

=> ∇ V (x,y,z) = (y² + 3z² x², 2xy+ ze^(-yz), 2zx³ - ye^-yz).

=> d/dt V (x,yz) = dV/dx * dV/dt + dV/dt * dy/dt + dV/dz * dz/dt

= (y² + 3z² x²) dx/dt + (2xy + ze^(-yz) dy/dt + (2zx³ - ye^(-yz)) dz/dt.

Jetzt ist das Problem, daß ich ja noch dx nach dt irgendwie unterbringen muss. Aber es taucht ja nirgendswo im Ausdrucke in "t" auf.
Unsere Tutorin meinte, dass x,y,z ja zeitabhängig sind und darin dann das t auftaucht. Als Hinweis hat sie uns noch an die Tafel geschrieben: dV/dt = dV/dx * dx/dt , wobei dx/dt = x' wär.
Ich bin verwirrt. Ich dachte dv/dx wär die Ableitung nach x.
Mir ist schon bewusst, daß wenn x,y und z zeitabhängig sind, dass dann so in die Richtung "Irgendwas mal t" geht, aber ich weiß nicht, wie ich das mathematisch ausdrücken soll.

ii) dh/dx = exp (-√(x-2,5)²+(y+3)² *(x-2,5)/√(x-2,5)²+(y+3)² - 0,2 (x+1,5)/√(x+1,5)²+(y-2)²

dh/dy = -exp (-√(x2,5)²+(y+3)² * (y+3)/√(x-2,5)²+(y+3)² - 0,2 (y-2)/√(x+1,5)²+(y-2)²

Jetzt wollen die aber bei dem Ort bestimme ne Koordinate hören.
Ich weiß aber nicht, was ich da einsetzen soll.
Google meint, man soll jetzt dh/dx und dh/dy schätzen bis x' = x+ Delta x und y' = y + Delta y und die Abstände infinitesmimal klein werden. Habt dann in dh/dx und dh/dy jeweils für (x,y) = (0,0), (1,1,) (-1,-1) und (3,3) eingesetzt. Kam ((-0,132802 ; -0,1146) , (-1,004 ; ,-0611), (-0,343 ; -0,118) und (0,010591; 2,55163) raus.
Und das ist ja auch nicht der wahre Hugo.

Mit freundlichen Grüßen,
Tobias Heinken

Da bei chemischen Reaktionen die schwache Wechselwirkung nicht beteiligt ist, sollten diese nicht nur CPT-invariant, sondern auch CP-invariant und sogar P-invariant sein. D.h. würde etwas dem entgegenstehen, dass sich aus gespiegelter DNA ein gespiegelter Mensch entwickelt, also ein Mensch, der das Herz auf der rechten und den Blinddarm auf der linken Seite, sowie alle sonstigen resultierenden Spiegelungen hätte (Milz auf der rechten Seite, R-Milchsäure wird schneller abgebaut als L-Milchsäure, usw.)?
(Die Fragen wurden so formuliert, dass der Nein-sage-Ablehnungs-und-Protesthaltungs-Reflex zu einer für mich positiven Antwort führt.)

Nabend, ich interessiere mich sehr für die theoretische Physik und Stand jetzt geht auch meine Berufswahl in diese Richtung... Welche Studiengänge stehen im engen Zusammenhang mit theoretischer Physik bzw. wo kann ich nach so etwas suchen (Website, App,...?)

Nicht viele Menschen kennen die String-Theorie, noch weniger kennen sich mit der Mathematik davon aus.

Deswegen möchte ich euch Profis fragen, stehen die Schancen gut das die String-Theorie stimmt ?

Damit ist nicht ein 100% beweis gefragt es geht mehr darum ob die Chancen für die Supersymetrie stimmen und alle andere Vorhersage die es für die String-Theorie braucht. Oder sieht es im Moment eher schlecht aus?

Grüsse

R

Es geht um Wasserstoff. Kann man eine 700 Bar Auslass einfach auf 350 Bar drosseln - mit einem Ventil oder so - oder ist der Druckunterschied hier zu groß?

Wenn man theoretisch Objekte schrumpfen könnte, dann sollten diese doch immernoch gleich viel wiegen wie vorher, weil man nur den Abstand zwischen dem Atomkern und den Neutron und dem Proton verkleinern würde.

Dadurch das man den Radius verkleinert und keine Teilchen verloren gehen, ist diese Annahme doch richtig?

Hey,

lasst mal euren Gedanken freien Lauf; was wäre gerade eine unglaubliche physikalische Erfindung, die quasi ein Durchbruch wäre,

Beispiel (was auch echt geht): Tag-Nacht-Solarzelle

Mal angenommen, wir haben in einem Volumen V N Atome. Die Anzahldichte ist ja dann

n = N/V

Wieso befinden sich in dem Intervall



insgesamt

Atome?

Es gibt ja eine niedrigste mögliche Temperatur (−273,15 Grad Celsius) weil die die Temperatur mit Teichenbewegung steigt und sie an diesem Punkt im kompletten Stillstand sind.

Eigentlich sollte es auch am anderen Ende eine Grenze geben, da die Teilchen sich nicht schneller als mit Lichtgeschwindigkeit bewegen können sollen.

Gibt es also eine?

Hallo,

Ich bin momentan auf Studiumssuche. Ich habe die letzen Wochen viel über Berufe in dem Bereich der Naturwissenschaften gelesen, sei es Astrophysik, Geophysik, Chemie, einfach Physik. Allerdings haben alle diese Studiengänge zwar ein ungemein spannendes Studium, aber sehr schlechte Berufsaussichten was meine Interessen angeht.

Mir ist bewusst, dass Naturwissenschaften selber eine gute Berufsaussicht haben, vor allem im Bereich der Industrie. Aber da liegt der Haken. Ich würde sehr ungerne in einem langweiligen Unternehmen arbeiten. Wenn, dann würde ich gerne in die Forschung. Mein Fokus liegt momentan auf der Erforschung des Weltraums, und da gibt es nun einmal nicht viele Möglichkeiten.

Von daher habe ich mir Berufe im Bereich der Technik (Bsp. Maschinenbau mit eventueller Spezialisierung auf Luft und Raumfahrttechnik oder Medizintechnik) angeschaut. Ich bin mir aber sehr unsicher ob ich genug für diese Jobs brenne.

Ich bin zwar sehr interessiert an Technik, aber ich bin nicht die Art Person die wirklich viel in ihrer Freizeit an Geräten herumtüftelt. Ich bin durchaus in der Lage sie zu bauen und anzuwenden, aber als Experten würde ich mich nicht einmal annähernd beschreiben. Ich werkle also nicht mit Maschinen herum. Von daher wirkt ein Technisches Studium sehr unpassend.

Ist diese Einschätzung richtig?

Stattdessen wünsche ich mir einen Job wo ich mit Hilfe dieser Maschinen Forschen kann, ich würde sie also viel lieber anwenden.

Gibt es irgendwelche Ideen was ich studieren und arbeiten könnte? Gibt es vielleicht etwas was mir bei der Entscheidung helfen kann?

Vielen Dank schon einmal und entschuldigt die lange Beschreibung xD

Frage steht ja schon da. Wenn ihr die Serie gut findet, dann schreibt bitte dazu warum. Gerne könnt ihr mir auch eure Lieblingsfolge nennen.

Wenn ihr die Serie nicht mögt, würde ich gerne wissen, warum ihr sie nicht mögt.

Danke für eure Antworten.

LG ChrystalDragon7 🍀

Übrigens: Option 5 könnt ihr wählen, wenn ihr das Konzept der Serie ganz gut findet, aber eine gewisse Person nervt oder wenn euch noch etwas anderes stört.

Hi, bei folgender Aufgabe ist die Rotation = 0, aber:

1. Das geschlossene Kurvenintegral der c) liefert 4*pi*I/c, nicht null.
2. Magnetfelder sind Wirbel.

Wie kann das sein?

Danke für Hilfe im Vorraus!

Damit möchte ich die erste und zweite Dimension in Frage stellen: was ist der Beweis, dass diese Dimensionen (1,2) überhaupt echte Dimensionen sind? Wieso "bekommt" man eine neue Dimension, wenn man eine Achse vom Koordinatensystem entfernt? Ist das nicht nur Mathe?

Kann es womöglich sein, dass es weitere Dimensionen unter unserer gibt, und wir zb. in der zehnten Dimension leben? Oder vielleicht gar in der ersten?

Laut Einstein leben wir ja sogar in der vierten Dimension, wegen der Zeit. Ich finde Einsteins Theorien sehr stimmig, aber muss Zeit gleich eine Dimension sein?

Ich habe mir den Luxus genommen und diese Fragen nicht vorher in google eingetippt. Hätte wohl eh nichts brauchbares ergeben, und ich weiss auch nicht wonach ich genau suchen soll.

Ich lese grad ein Buch, wo es um das berühmte Werk "Flatland" von E.A.Abott geht. Höhepunkt: Die zweidimensionalen Wesen in Flatland erleben den Durchgang einer Kugel durch ihre flache Welt als einen grösser und kleiner werdenden Kreis, der wie aus dem Nichts erscheint.

Überlegung dazu: Die Flatlander, so es sie gäbe, könnten doch nur eindimensional sehen ( Linien), denn man muss ja dreidimensional unterwegs sein, um zweidimensionale Formen erblicken und sie als solche erkennen zu können. Die Sichtweise eines Flatlanders müsste eindimensional sein, denn ihre Augen liegen auf einer der beiden Linien Länge/Breite ihres Körpervierecks/Körperdreiecks. Sie müssten den Durchgang einer Kugel durch ihre Welt als auftauchende Linie, die breiter und schmaler wird, sehen und nicht als Kreis.

Umgerechnet auf unsere Verhältnisse: Damit wir drei Dimensionen mit einem dreidimensionalen Auge sehen können, braucht es dazu nicht einen vierdimensionalen Raum (Hyperkubus)?

Habt ihr schonmal von Robert Oppenheimer gehört der zu den Erfindern der Atombombe zugerechnet wird? Danke für eure Antworten.

Zwerg-Riese und weißer Riese?

Also mag jetzt etwas banal klingen, aber der Herr im folgenden Video hat seine Professur in der theoretischen Physik mit Schwerpunkt Astrophysik an der Harvard School absolviert und legt die verschiedenen Sternarten dar.

Und von einem Zwerg Riesen habe ich noch nicht gehört, was ist das?

Siehe Frage

Wenn ihr auch grobe Gehaltsperspektiveb habt, wäre ich dankbar.

Hi, wir haben in Experimentalphysik 1 folgende Aufgabe bekommen:

Leider war der Ex1 Prof etwas voreilig. Wir hatten in HöMa/Theo noch keine Vektorfelder, Linienintegrale etc... Das kann ich größtenteils schon alles über Bücher/Google beziehen.
Wo ich allerdings noch Hilfe bräuchte:

Wie setze ich den Ort r(t) überhaupt in das Kraftfeld/Fläche ein?
Kann ich einfach die Parameter der Einheitsvektoren, für y und x einsetzen?

Vielen Dank für Hilfe im Voraus!

Hallo zusammen,

ich bin dabei eine DGL mit Hilfe der Variation der Konstanten zu lösen, ich glaube ich habe soweit auch eine Lösung für die DGL; jedoch hänge ich irgendwie komplett mit den Anfangsbedingungen die uns gegeben sind:
x(0)=0 und x'(0)=-A/2
Was genau mach ich mit den Bedingungen, setze ich diese für y(x) und y'(x) jeweils ein und löse dann nach den konstanten auf? Die DGL und meine bisherigen Notizen sind im Bild zu sehen:

Hi, ich habe das Bild von der Aufgabe angefügt, mit der ich ein Problem habe.

1. Wieso definiert sich v0 durch v/sqrt2 ?
2. Wieso findet sich m im Nenner des Fg Summanden wieder? Die zweifache Integration von Fg müsste doch x+vt+(1/2)Fgt^2 sein. Woher kommt m im Nenner? Somit ergibt x''(0)= (1/m)Fg und nicht Fg, wie es in (a) bestätigt werden soll.

Vielen Dank im Voraus für Hilfe!

Wie lernt man es am besten?

In was für einer Reihenfolge sollte man die Themen lernen? bzw.

Gibt es eine Roadmap dafür

Was macht dieses Defragmentieren ? Wofür ist es gut ? Werden Daten dadurch gelöscht ?

Gibt es physikalische Theorien, die beschreiben, was vor dem Urknall sein könnte?

Das Problem ist, dass man immer auf belanglose Theorien wie dem Big Crunch, etc. stößt, dass im Grunde genommen überhaupt nichts mit der Fragestellung zu tun haben.

Also es geht mir nicht darum, dass unser Universum eventuell aus einem anderen entspringt oder dass unser Universum ein schwarzes Loch ist oder dass es mehrere Universen gibt in einem Multiversum oder die Viele Welten Theorie,

All das sind Theorien, die absolut und rein gar nichts mit der Fragestellung zu tun haben.

Meine Frage lautet also, ob es physikalische Theorien gibt (oder eventuell eure), was der Ursprung vom Urspung ist. Also selbst wenn es davor 100 andere Universen gibt oder wir in einer Simulation leben, muss es ja ein davor geben.

also haut eure theorein raus

Waagen auf der Erde messen die Kraft, die durch einen Körper im Gravitationsfeld der Erde wirkt geteilt durch 9,81m/s^2.

Mir ist der unterschied zwischen Trägheit und Gewicht schon bewusst. Auf der Erde sind beide numerisch gleich.

Aber warum sagt man nicht einfach:

Ich will Rindfleisch im Wert von fünf Newton kaufen.

Anstatt das man ein halbes Kilogramm haben will?

Egal weshalb, glaubt ihr daran?

Könnt ihr mir eine schwere Mathe und-oder Physik Aufgabe stellen. Also eine Gleichung oder änhliches.

Hallo,

ich befinde mich in der Q1 (12. Klasse Gymnasium) und ich muss in Mathe eine Facharbeit schreiben.

In meiner Facharbeit habe ich den Themenschwerpunkt Physik und will das Thema "Wozu brauchen wir n-dimensional Räume?" aufgreifen und halt die Anwendung davon.

Unser Lehrer meinte, dass wir einen Experten in dem Fachgebiet befragen dürfen, der uns bei der Auswahl für die richtige Fachliteratur berät und wir das dann auch in der Arbeit erwähnen können.

Also wenn jemand, der dies hier gerade liest, ein Experte in Physik/Mathe ist (oder am besten sogar einen anerkannten Titel darin hat), wäre es sehr freundlich, wenn diese Person mir gute Fachliteratur für meine Facharbeit empfehlen würde. Dann kann ich diese Person mit Namen (und Titel) nämlich in der Arbeit erwähnen und habe zusätzlich eine gute Auswahl an Informationsquellen.

Ich wäre jemanden, der mir hierbei hilft daher sehr sehr Dankbar.

Danke schonmal im Voraus!

Hi,

bin etwas verwirrt von der Levi-civita-notation. Wenn ich zwei epsilon-tensoren multipliziere:

Wie lese ich das dann ohne Informationen über die Indizes zu haben? Woher soll ich wissen, wann zB i und l gleich sind?

Gibt es Stoffe die bei einer höheren Temperatur brennen , als die Temperatur wo die Stoffe nicht vom Sauerstoff getrennt sind und Thetmolyse eingehen ?

Hallo,

ich sitze hier vor einer Aufgabe, bei der man den Trägheitstensor eines Drahtes bestimmen soll. Der Draht ist wie in der Abbildung geformt und die Dichte für die eingezeichnete Komponente (Rho 1) ist wie folgt gegeben:



Nun muss ich die anderen Komponenten der Dichte bestimmen, um damit die Trägheitsmomente zu berechnen. Leider verstehe ich die Formel nicht ganz und komme deshalb nicht auf die anderen Komponente, kann mir jemand helfen, die Formel zu verstehen?

Danke im Voraus!

PS: Die Thetas in der Formel bezeichnen die Heaviside-Funktion.

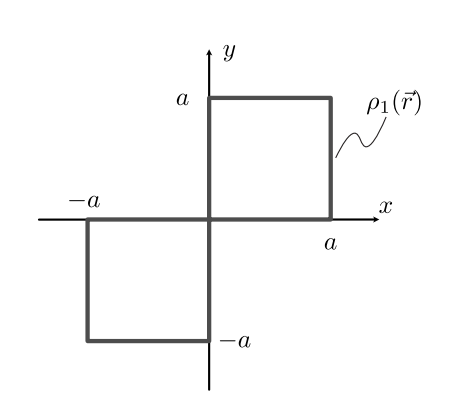
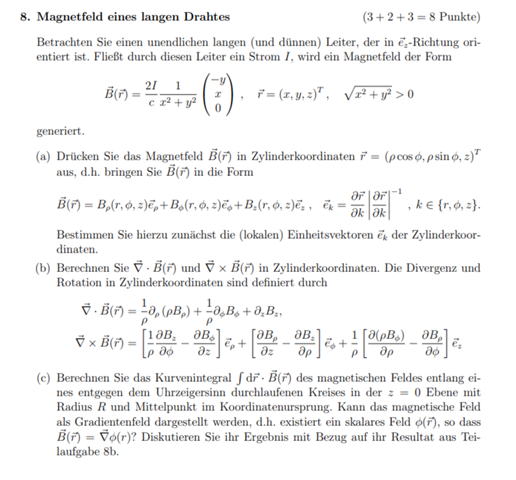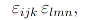Hallo,

ich hänge gerade an dieser Aufgabe:

"Welche Arbeit wird von den Kraftfeldern (K_1, K_2) bei einem Umlauf um das Einheitsquadrat verrichtet?"

Ich blicke bei dem Thema noch nicht so ganz durch, also urteilt nicht zu hart!

In der a) habe ich berechnet, dass K_1 nicht konservativ und K_2 konservativ ist.

Für K_2 habe ich dann auch das skalare Potential berechnet (K_1 hat ja kein skalares Potential, da es nicht konservativ ist, oder?)

Nun soll ich also die Arbeit berechnen. Dazu muss ich das Arbeitsintegral bilden.

Für K_2 war mein Ansatz:



wobei ich irgendwie den Weg als Vektor r(t) angeben wollte, um dann zu berechnen:



allerdings weiß ich nicht, ob der Ansatz richtig ist und was dann r(t) und die Grenzen des Integrals wären (von 0 bis 0?).

Bei K_1 hätte ich das auch so versucht, bin mir aber unsicher, ob es da nicht einen Unterschied gibt, weil K_1 ja wegabhängig ist, weil es nicht konservativ ist.

Vielleicht ist mein Gedankengang auch völlig daneben.

Hilfe wäre schön, Danke im Voraus und LG!

Hallo. Ich (M/15) habe gerade die glorreiche Idee bekommen Rick and Morty, die nächsten Stunden, durch zuschauen. Aber da ist mir eingefallen, dass die Serie ja sehr viel mit theoretischer Physik oder ähnliches zu tun hat. Sollte ich die Serie demnach lieber nicht schauen, weil ich die Witze, die implementiert wurden, nicht kapieren werde?

Hey,

ich habe dieses Jahr Matura, was bedeutet, dass ich im Oktober 2022 zu studieren beginnen würde. Da ich mich zu 99% für Physik entscheiden würde (im Master dann vermutlich Astro- oder Theoretische Physik), wollte ich fragen, welche der beiden Unis (TU München oder LMU) „besser“ für meinen Studiengang wäre. Außerdem würde mich interessieren, ob es sich auszahlt bereits für den Bachelor nach München zu gehen, oder ob es erst wirklich aus finanzieller Sicht (wohne in der Nähe von Wien) sinnvoller wäre für den Master nach München zu gehen. Da man sich -so wie ich das verstanden habe- im Bachelor sowieso eher auf die Basics spezialisiert, gäbe es ja wahrscheinlich keinen allzu großen Unterschied zwischen den Unis in Wien und in München (im Bachelor), oder liege ich da falsch?

Außerdem wollte ich fragen, ob es unter den Lesern Leute gibt, die eine ähnliche Erfahrung gemacht haben, und mir eventuell Tipps geben könnten, wie ich mit diversen Auslandsstudium-Programmen Geld sparen könnte, oder allgemein Tricks anwenden könnte um Geld zu sparen (München ist ja nicht gerade billig).

Danke schon mal im Voraus

Was meint Einstein damit, dass Gott nicht würfelt?

Gibt es eine Erklärung von ihm?

Falls nein, gibt es eine "allgemeine" Erklärung, oder interpretiert jeder etwas anderes?

Es sollen wohl Quanteninformationen aus einem Schwarzen Loch übertragen werden aber mir erschließt sich nicht die Bedeutung des Anfangs der Nachricht

..-. .-.. ---

Weiß jemand ob es physikalisch sinnvoll anfängt oder der Anfang eine bestimmte Bedeutung z.B. für den Autor des Drehbuchs ect. hat?

Hallo,

ich bereite mich zur Zeit auf eine anstehenden Prüfung vor. Ich komme bei der Bearbeitung dieser Aufgabe (c) leider nicht weiter. Die Teilaufgaben a und b müssten richtig sein. Bei der c) habe ich noch eine Rechnung, die von irgendeinem Studenten mal gemacht wurden. Ich weiß nicht ob ihre Rechnung stimmt, habe versucht nachzuvollziehen was sie da rechnet (daher die bunten Markierungen). Könnte mir da vielleicht einer bitte weiterhelfen.

Danke im voraus.

Hallo, ich habe vor kurzem mein Abitur absolviert und ich würde bald gerne Physik studieren (nicht Lehramt).

Soweit ich mich informiert habe, ist das Studium bis zum Bachelor überall nahezu gleich. Nach jetzigem Stande würde ich zum Master hin gerne in Richtung theoretische Physik gehen (ich bin mir jedoch bewusst, dass sich das höchstwahrscheinlich auch noch ändern kann, z.B. Experimentalphysik).

Das Ding ist, ich möchte nicht Physik studieren um Karriere zu machen und viel Geld zu verdienen, ich würde gerne in die Wissenschaft gehen und stattdessen der Welt einen Beitrag für die Wissenschaft leisten.

Ich bin niemand der sich total sicher mit der Materie auseinandersetzt, jedoch lese ich viel Literatur über Physik, habe in den letzten Jahren großes Interesse dafür entwickelt (meines Erachtens nach leider erst etwas spät) und unterhalte mich gerne mit Physik-Studenten /Interessenten über physikalische Probleme/ Ereignisses etc.

Hat jemand von euch ebenfalls aus dem selben Grund Physik studiert oder ist gerade dabei und kann mir von seinen Erfahrungen berichten?

Lg

Weiß ich einer vielleicht wie man die Wurfkraft über einen Weg von s=1m berechnet? Die einzige Formel die mir da eingefallen ist die der Arbeit. W=Fs. Es geht um die c). Die a) und b) habe ich gelöst. :)

Es geht um folgende Aufgabe:

Schwingungen sind leider nicht so meine Stärken. Wenn mir da einer bitte 🙏 weiterhelfen könnte diese Aufgabe zu lösen. Ich schreibe in einigen Tagen eine Klausur :/

Das sind meine Ansätze:

a)

c) Ist das damit gemeint?

Bei der b) habe ich keinen Ansatz.

es geht um die a)

also ich habe mir folgendes gedacht. Das Trägheitsmoment eines Quaders bzgl der Schwerpunktachse zu berechnen und dann den Satz von Steiner anzuwenden. Anschließend das Ergebnis mal 3 nehmen, da wir 3 Flügel (Also 3 Quader haben).
jedoch bin ich mir nicht sicher wie die Höhe des Quaders zu bezeichnen ist, deswegen habe ich sie c genannt. Oder ist damit d gemeint?

meine Skizze (rechts):

Meine Lösung:

Hallo liebe Communtity,

ich bin zwar erst 15, habe aber seit Jahren schon das Ziel, theoretischer Physiker zu werden. Daher beschäftige ich mich schon seit Jahren mit Mathe aus meinen zukünftigen Klassen und auch weiter. Ich habe letztens das Buch Rechenmethoden für Studierende der Physik im ersten Jahr gekauft, und dort fast alles verstanden. Also denke ich, dass ich nun ein Buch verstehen könnte, dass zeigt, wie man Probleme theoretisch löst, wissenschaftlich arbeitet und natürlich auch Physik erklärt. Ich wäre froh, wenn es überhaupt so etwas gäbe, weil meine Suche hat leider nichts ergeben :(

Grüße aus NRW!

Leider haben wir in der Vorlesung nichts erhalten, was uns helfen könnte, dieses Problem zu lösen. Hat jemand Literatur oder ein Video oder eine gescheite Hilfe parat, dass zeigt, wie ich hier vorgehen muss?

Wäre nett wie man auf die Lösung schritt für schritt kommt.

Danke

Kann mir bitte jemand bei dieser Frage helfen? Ich checke es nicht, wie löst man?

Was wäre die Antwort wenn man 60km/h schnell gefahren würde?

Müsste die Antwort hier nicht 25 sein? Weil ja soweit ich weiss rechnet man so:

50 kmh ÷ 10 x 50 kmh ÷ 10 = 25

Bei Zeitreisen sagt man es ist unmöglich, dass sich zwei Körper zur selben Zeit am selben Ort aufhalten.

Gilt das aber auch für Paralleluniversen?

Guten Morgen liebe Gutefrage Community :)

Aus Gründen meines Studiums der Theologie sowie meiner (bislang) privaten Beschäftigung mit der Philosophie, interessiere ich mich zunehmend für zeitgenössische Theorien der theoretischen Physik, welche den Anspruch haben, den Ursprung des Universums zu erklären und dabei eine "Theorie von Allem" zu bilden. Wie es scheint, sind theoretische Konstrukte wie die Relativitätstheorie sowie die von ihr ausgehende String-Theorie in ihrer Tiefe derart komplex, dass sie nur von wenigen Spezialisten verstanden werden. Ich würde vor Allem gerne verstehen, wie Physiker zu der Aussage kommen, dass der Urknall die simultane Entstehung von Raum und und Zeit sei, bzw. warum man postuliert, dass Zeit ontologisch 'Etwas' sein müsse, was 'atemporal' entstehen kann?

Meine Frage an die Physiker/innen unter uns lautet nun ganz konkret: Hat man als Laie eine Chance, sich ohne ein universitäres Studium das nötige physikalische Grundwissen anzueignen, um Fachbücher zu dem Thema auch nur annähernd gut verstehen zu können? Und gibt es gute Bücher/ Videos für absolute Physik-Laien, welche nichtmal die einfachsten Formeln kennen, um einzusteigen und sich auf Universitäts-Niveau zu steigern? Mir reichen die populärwissenschaftlichen Vereinfachungen um ehrlich zu sein nicht aus, da ich das Gefühl habe, dass ich ohne ein Verständnis der physikalischen Grundlagen nicht hinter die den Theorien zugrundegelegten Prämissen blicken und diese bewerten kann.

Vielen Dank im Voraus und einen guten Start in den Tag,

Heuschrecke 001

Wenn man in einem Fahrzeug wäre, das mit Lichtgeschwindigkeit fliegen würde, und man sich dann in dem Fahrzeug nach vorne bewegt.

Würde man sich dann nicht mit Überlichtgeschwindigkeit bewegen?

Was ja eigentlich nicht möglich ist...

Hallo gf Community,

Also ich habe mir folgendes vorgestellt:

Man hat einen geschlossenen Raum ohne Fenster, “Spalten”, oder sonstige Öffnungen, durch welche das Licht hinaustreten kann.

An der Decke hängt eine Lampe oder irgendein leuchtendes Objekt.

Wenn man das Licht einschaltet, dann ist der Raum logischerweise hell erleuchtet.

Was passiert aber mit dem Licht, wenn man die Lampe wieder ausschaltet?
Die Wellen/Teilchen (was auch immer) können doch nicht einfach verschwinden und sich in Luft auflösen ?

Jetzt könnte man sich denken, dass es einfach kein Licht gibt, ohne das Objekt, welches das Licht aussendet.

ABER: wenn zB ein Stern “stirbt”, dann kann man auf der Erde auch nach tausenden von Jahren noch das Licht des damaligen Sterns beobachten. D.h. hier verschwindet das Licht eben nicht einfach so.

Was passiert also mit dem Licht im geschlossenen Raum?

Wäre sehr über logische und hilfreiche antworten dankbar 😅 vllt ist diese Frage sehr banal und lächerlich, aber joa .. kann es mir halt nicht erklären

Hallo, ich lese aktuell ein Fachbuch über Quantenmechanik und befinde mich im Kapitel Drehimpulse und Spins. Genauer geht es aktuell um Spinaddition. Da ich mir am Ende des Kapitels nicht sicher war, ob ich alles verstanden habe, habe ich einen Blick auf die Übungsaufgaben geworfe. Dort findet sich die auf dem Bild zu sehende Übungsaufgabe, die ich gerne lösen würde, aber ich bin mir noch nicht ganz sicher wie.
Thematisch geht es um die Addition der Spins von zwei Teilchen. Weil der Spin s=1/2 ist, gibt es für jede komponente des Spinoperators genau zwei Eigenwerte (+h/2 und -h/2). Auch ist mir bewusst, dass die spinoperatoren unterschiedlicher komponenten von verschiedenen Teilchen vertauschen (also [s_x^1,s_y^2]=0). Weiter kann ich die die Komponenten des Spinoperators (also s_x;s_u;s_z) also 2x2 Matrix schreiben. Wie kann ich aber nun diese Matrix auf ein Teilchen "münzen". Ich gehe davon aus, dass ein Teilchen spin up hat und das andere spin down. Muss ich nun die Erzeugungs/Vernichtungsoperatoren für den Spin (auch Leiteroperatoren genannt (s_+ und s_-); die auch auch als 2x2 Matrix darstellen kann) auf die komponenten der Spinoperatoren anwenden, also damit ich einem Teilchen spin up und dem anderen spin down verpassen kann?
Also wäre so etwas für den ersten Additionstherm korrekt?:
s_+*s_x*s_-*s_x (natürlich alles in Matrixform)

Da ich selbst an diesem Beruf interessiert bin habe ich eine Frage: Was macht man als Theoretischer Physiker den ganzen Tag? Ich kann mir nämlich nicht vorstellen, dass es so aussieht wie bei The Big Bang Theory, wo man den ganzen Tag nur in einem Büro steht, nachdenkt und ab und zu etwas auf eine Tafel schreibt/rechnet.

Hi. Also ich will später eventuell theoretischer Physiker werden ich verstehe ob ich das Gehalt 30,100 Euro Gehaltsanstieg ist das ,aber bekomme ich monatlich oder jährlich das Gehalt.

https://www.mystipendium.de/studium/theoretische-physik#Theoretische%20Physik-studium-in-zahlen

Da steht das nochmal,

Was genau ist die Plack-Länge und wie wird sie gemessen? Bitte so einfach wie möglich erklären, ich Interessiere mich zwar extrem für solche Themen aber bin erst 15 und mein Wissen in diesem ist nicht ziemlich ausgeprägt😅

Ich habe mich gefragt, wie das individuelle Ich, die Seele und das Bewusstsein eines Menschen entstanden ist. Also warum bin ich ich und nicht mein Nachbar ;)

Daher bin ich zu dem Schluss gekommen, dass das individuelle "Ich, die Seele und das Bewusstsein" eine untrennbare Einheit mit dem Gehirn bilden und jedes Gehirn ist einzigartig.

Und dass der Mensch doch aus der Vermischung aus Samen und Eizelle, also einer Art Ursuppe entstanden ist, die die Eigenschaft hat ein Bewusstsein zu bekommen.

Man müsste doch in naher Zukunft einen Menschen auch künstlich herstellen können.

Symbolisch: Man hat eine Flasche Fanta, in ihr stecken künstliche weibliche Supergene, und in der Flasche Cola stecken männliche Supergene. Schüttet man sie zusammen, hat man eine Pfütze die ein Bewusstsein bekommt, und aus der unter bestimmten Brutbedingungen ein Mensch heranwächst.

Hat dann dieser künstliche Mensch, der ohne Mutter gebrütet wurde, auch ein Bewusstsein und eine Seele, oder wird er eine Art Zombie ohne Seele werden ?

Haltet ihr das alles für möglich und logisch?

Gibt es das alles schon ?

Was ist der Unterschied zwischen den dreien ?

Und wird man das alles in der Zukunft mal in der Raumfahrt anwenden können, zum Beispiel als Antrieb für ein Raumschiff ?

Hallo, vielleicht kann mir jemand bei einem Problemchen aus meinem Lehrbuch zur theoretischen Mechanik helfen: Ein kugelförmiger Wassertropfen mit Radius R, Volumen V und Masse m soll fallen, wobei seine Masse wegen des Wasserdampfes proportional zu seiner Oberfläche anwächst. Auf ihn soll neben der Schwer- eine Reibungskraft wirken, die ich aber erst mal außen vor lassen will.

Es ist also(x-Richtung nach unten, dx/dt=:v, dv/dt=:a) dp/dt = mg, d.h. (dm/dt)v + ma = mg

Es ist dann wohl dm/dt = cpiR^2, wobei R von t abhängt. Dann ist ja m-m_0 = c*pi*1/3 R(t)^3

Die Bewegungsgleichung soll integriert werden, indem R anstelle von t als unabhängige Variable eingeführt wird. Ich weiß aber gerade nicht, wie ich da vorgehen soll.

Die Frage ist eigentlich ganz einfach: Was ist das?

So wie ich das bisher verstehe geht es in erster Linie darum in Formeln, die von der Zeit abhängig sind, die Zeit mit der imaginären Zahl i zu multiplizieren, um dann auf irgendwelche anderen Formeln zu kommen, aus denen das i dann einfach wieder weggestrichen wird. Benutzt Stephen Hawking das wirklich nur als einen "Rechentrick" oder hat er sich dabei vielleicht doch etwas mehr gedacht? (wovon ich mal ausgehe^^)

Folgt aus einer Existenz von imaginärer Zeit dann auch komplexe Zeit, quasi eine Art Zeitebene? Wenn dem so ist, wie kann man sich das vorstellen, welche Konsequenzen hätte das?

Tut mir Leid, ich interessiere mich rein privat dafür und habe keinen wissenschaftlichen Hintergrund in der Physik. Wenn mir das jemand also leihengerecht erklären könnte, wäre ich sehr dankbar :)