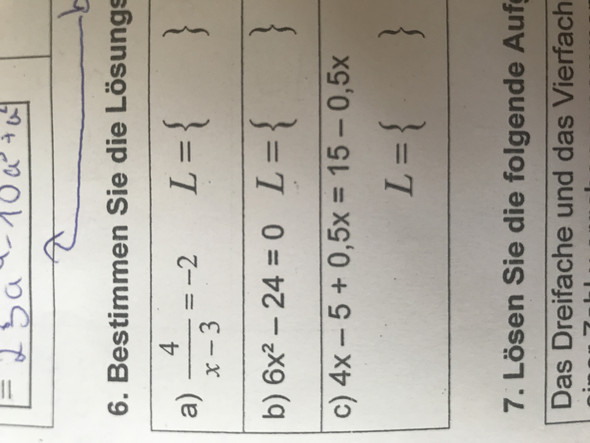
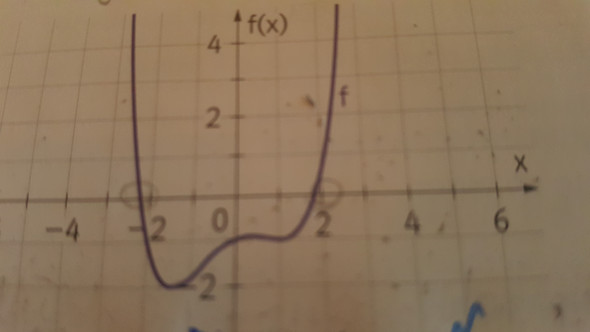
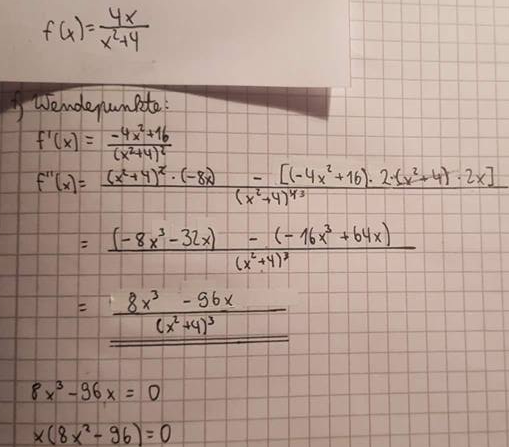Hey, ich schreibe morgen eine Matheklausur zu "Verknüpfung von Funktionen und Wachstum" und stehe bei einer Aufgabe gerade echt aufm Schlauch. Sie lautet:
"Eine Firma berechnet die täglichen Verkaufszahlen eines Handymodells, das neu eingeführt wird, modellhaft mit der Funktion f(t)=20 * (t-15) * e^(-0,01t) +300 (t: Anzahl der Tage nach Einführung des Modells). Sie erwirtschaftet einen Gewinn, wenn täglich mehr als 450 Handys verkauft werden. Berechnen Sie die Länge des Zeitraums, in dem ein Gewinn erwirtschaftet wird."
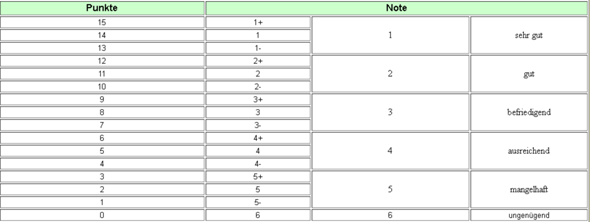
Die Antwort in den Lösungen dazu ist:
"Nach etwa 25 Tagen erwirtschaftet die Firma einen Gewinn durch den Verkauf des Handys. Nach etwa 392 Tagen sinken die Verkaufszahlen so stark, dass die Firma keinen Gewinn mehr erwirtschaftet. Die Firma erzielt demnach für etwa 367 Tage, also für etwas mehr als ein Jahr, einen Gewinn."
(Mein Mathebuch ist übrigens "Lambacher Schweizer - Mathematik Qualifikationsphase - Grundkurs" vom Klett-Verlag und die Aufgabe steht auf Seite 56.)
Ich habe versucht, die Gleichung mit der 450 gleichzusetzen und dann auszurechnen, aber das hat nicht funktioniert. Ich war so verwirrt, dass ich an der Stelle nicht weiter gerechnet habe, weil ich nicht wüsste wie.
Vielleicht habe ich mir irgendwo einen Denkfehler erlaubt oder ich war auf einem ganz falschen Weg. Wenn jemand weiß, wie man das rechnet (und mir möglichst noch vor morgen 7:50 Uhr antworten kann), wäre ich echt dankbar für jede Hilfe!
Danke schon mal im voraus! <3