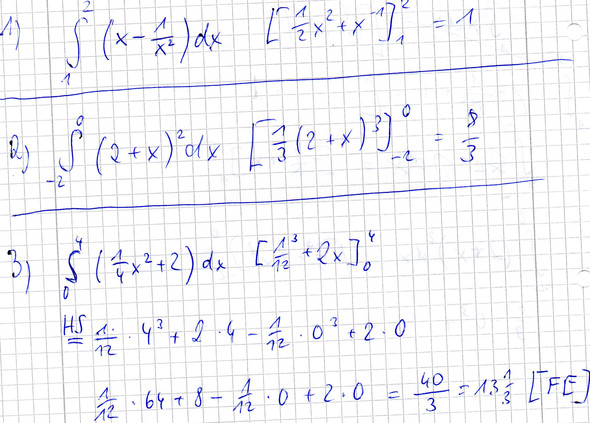Integralrechnung – die neusten Beiträge

ich weiß nicht wie man auf die Gleichung g und h kommt Bei g weiß ich nur den Ansatz g(x)=a*x^2+5 aber wie kommt man auf a und h(x)? Bitte schnell Hilfe und eine Erklärung die Idiotensicher ist :D

Hallo, wäre nett wenn jemand mir den kompletten Rechenweg sehr verständlich darstellen würde

Was muss ich beachten, wenn zum Beispiel ein Intervall von (-1;2) angegeben ist und die Funktion 1/6x^3 - 1/2x ist? Ich bräuchte nur kurz eine Vorgehensweise, besonders wie ich mit dem Intervall umgehe.

Gegeben ist die Funktion f(x)=3-3x^2. Ich habe bereits die Nustellen berechnet sowie die Stammfunktion gebildet. Mithilfe dieser habe ich dann durch Integrieren einen Flächeninhalt von 4 erhalten. Nun wird diese Parabel aber von einer horizontalen Geraden halbiert und wir müssen herausfinden, wo genau diese liegt. Kann mir bitte jemand erklären, wie das geht? Danke im Voraus!

Kann mir jemand bei der auf dem Bild zu sehenden aufgabe helfen ?

Ich weiß, wie ich auf die Flächen A1 A2 A3 und A6 als ganzes komme, aber nicht wie ich diese dann unterteile.

Danke schonmal.

Hey könnt ihr mir helfen, Hafensänger? Ich habe ein Bild und brauche eine Funktion die sich derer im Bild annähert. Es handelt sich um ein Bierglas

Gesucht ist die Stammfunktion von 8ax^3. Aber was bedeutet a?

Hallo :-) Wie gehe ich die Aufgabe 11 an?

Hallo, ich habe hier drei Aufgaben zur Integralrechnung. Aufgabe 3 konnte ich ohne Probleme lösen, aber bei 1 und 2 liegt mir zwar die Lösung vor(steht hinter der Aufgabe), allerdings bekomme ich das nie raus. Ich weiss nicht, wie ich mit dem x-1/x^2 und (2+x)^2 verfahren muss. Ich habe echt alles versucht, ich rechne mich hier dumm und dämlich, kann mir hier vielleicht einer bei dem Lösungsweg helfen? Ich hab leider echt ne Menge von diesen Aufgaben, und ich wünschte, es wären alle so leicht wie die dritte. Aber es muss doch ähnlich funktionieren!? Wäre sehr nett, wenn mir jemand helfen würde.

Hallo,

ich habe heute erfahren, dass wird morgen einen Test in Mathematik zum Thema der Integralrechnung schreiben und leider kann ich das nur minimal. Könnte mir jemand sagen und vielleicht erklären, wie die Stammfunktion zu f(x) = 3/x^2 lautet und warum?

Danke im Voraus,

Justin S.

Die Angebotssfunktion lautet: Pa(x)= 0,1x^2+2 Die Nachfragefunktion lautet:Pn(x)= -1x+10

Ein Tank enthält zu Beginn (t=0) zwei Liter Benzin. Es wird nun getankt. Die Zuflussrate in Liter pro Sekunde (l/s) kann für einen Zeitraum von 0 < t < 10 näherungsweise durch die Funktion f(t) = -0,03t^3 + 0,3t^2 beschrieben werden.

a.) Wann ist die Zuflussgeschwindigkeit am größten?

b.) Wann nimmt die Zuflussgeschwindigkeit am stärksten zu?

c.) Wie viel Liter Benzin befinden sich nach 5s im Tank?

d.) Wie viel Liter Benzin sind in den ersten 5 Sekunden durchschnittlich in den Tank geflossen?

Hey ihr, meine Aufgabe ist es herauszufinden wie viel Sand zum Bau einer Rampe benötigt wurde. Ich habe die Rampe ausgemessen.Nun soll ich mit den Mitteln der Integralrechnung und den Querschnitssfunktionen das Volumen berechnen. Ich weiß aber nicht was das überhaupt ist. Danke schonmal und LG.

Hallo :-)

Kann mir jemand bitte diese Aufgabe erklären?

Das Integral von v(t) also der Flächeninhalt unter einer "Geschw. - Zeit" Funktion ist bekanntlich der insgesamt zurückgelegte Weg. Was ist aber dann das Integral einer a(t) bzw. v'(t) also einer Beschleunigungs - Zeits funktion?

Hallo, ich muss zum folgenden Bruch eine Stammfunktion angeben: x hoch3 +1/ 2x hoch2

Weiß jemand wie ich das machen kann, wenn x sowohl im Zähler als auch im Nenner vorhanden ist? Wenn es nur im Zähler ist, dann geht's ja noch. Hab im Internet schon gesucht, aber nicht wirklich was gefunden

ich muss ein bestimmtes Integral ausrechnen, dabei sind die Grenzen 0 und pi/2. Rauskommen sollte -1

Hey, ich weiß das Thema gibt es schon ziemlich oft aber ich verstehe es einfach nicht. Ich habe folgende Funktionen: f(x)=3x+1 und g(x)=x^2+3. Als erstes müsste ich ja jetzt die Schnittpunkte berechnen und danach die obere Funktion von der unteren subtrahieren. Hier liegt aber mein Problem wie gehe ich hier vor? f(x)-g(x)=(3x+1)-(x^2+3) Das Ergebnis ist -x^2+3x-2 Wie ich auf die -2 komme weiß ich auch aber die x irritieren mich :( Danke schon mal im voraus

Hallo. Wie rechne ich diese Aufgabe zuende ?

Bestimme die Intervallgrenze u des Intervalls I so , dass der Graph von f mit der x-Achse über dem Intervall I eine Fläche mit dem Flächeninhalt A einschließt.

f(x)= x+2 F(x)= 1/2x^2 + 2x

Intervall [1;u]

A= 13,5

Ich weiß ,dass die Lösung 4 ist ,aber komme rechnerisch nicht darauf.

Ansatz:

F(u) - F(1) = 13,5 1/2u^2 + 2u - (1/2x1^2 + 2x1) = 13,5

= 1/2u^2 + 2u -2,5 = 13,5 | +2,5

= 1/2u^2 + 2u = 16 |

= u(1/2u + 2) = 16

x1= 0

x2 = 1/2u + 2=0 | -2
= 1/2u -2 | :1/2
= u -4

Das Ergebnis soll aber +4 lauten. Was hab ich falsch gemacht ?

(1. Bild) Aufgabenstellung: Lösen Sie folgende unbestimmte Integrale:

Soll ich hier einfach nur die Stammfunktion bilden? Ich weiß immernoch nicht wirklich, was unbestimmte Integrale sind.(2. Bild) Falls ich nur die Stammfunktion bilden sollte, sind dann meine Lösungen richtig?

Wenn einer dies Schritt für Schritt ausrechnen könnte wäre ich sehr dankbar, danke ;)

Hallo hat jemand eine Idee wie diese Aufgabe zu lösen ist. Anbei ist noch das Zeit-Geschwindigkeitsdiagramm.

Ein Fallschirmsprung wird in vier Phasen untergliedert. Die Geschwindigkeiten vI (t) und vIII (t) der Phasen I und III lassen sich näherungsweise durch eine Potenzfunktion 3.Grades der Form f(t) = at3 darstellen.

Ermittle vI (t) durch Verschieben des Terassenpunktes T (0Ι0) von Gf in den Punkt P (16Ι60) und mithilfe von vI (0) = 0.

Danke für Eure Vorschläge :-)

Hallo liebe Community, wir sollen folgende Aufgabe lösen: Es sei die Funktion f(x)=x^3 gegeben. Eine Parallele zur x-Achse soll jeweils konstruiert werden, sodass gilt: A1=A2. Das gilt jeweils im Intervall [0,1]. Brauche nur irgendwie einen Ansatz wie ich das lösen könnte. Wenn ich die Grundidee habe, kriege ich den Rest auch hin. Danke schon einmal im Voraus!

Was will mir dieses Zeichen sagen. Ich kanns halt nicht mal googlen, weil ich den Namen nicht kenne und ich das Zeichen nicht mit meiner Tastatur eingeben kann.
Gemeint ist der lange, gebogene Strich

Hi, mal ne Frage zu dem Integral von sin mal cos. Wenn ich partiell integriere bekomme ich ja je nachdem wie ich u und v´ wähle, einmal -0.5cos^2(x) und einmal 0.5sin^2(x) als Ergebnis. Das sind doch aber zwei unterschiedliche Werte am Ende.Wie sollte ich u und v´ denn wählen?

EDIT// OK hat sich geklärt. Sorry

Guten Abend,

ich möchte gerne wissen, wie ich das dx beim Integrieren behandelt, also, soll es eine Konstante sein, da die ja beim Integrieren wegfällt, oder soll es so etwas wie eine Unbekannte sein, beim Integrieren würde ja 1 rauskommen.

Ich habe nämlich eine Aufgabe gerechnet und du= 1/2 x dx herausbekommen.

Jetzt weiß ich nicht, ob da 1/2 rauskommt oder beides Weg fällt (in dem Fall wäre dx eine Konstante).

Wozu benötigt man die Integralrechnung in der Physik ich muss in Mathe einen Vortrag darüber halben und habe kein Physik mehr.
Danke im Voraus

Ich bräuchte Hilfe bei diesem Beispiel:

Die Kurven f(x) = x^2-4 und g(x) = -2x^2+8 schließen eine Fläche ein. Diese Fläche rotiert um die y-Achse. Berechnen Sie das Volumen.

hallo zusammen, ich schreibe demnächst eine Klausur zum großen thema integralrechnung und es harpert leider bei einer aufgabe, ich hoffe, dass mir dabei vielleicht jemand helfen kann

Gegeben ist die Funktion f mit der gleichung f(x)=-x^3+3x+2 a) Bestimmen sie den inhalt der Fläche zwischen dem Graphen von f und der x-achse im intervall [-2;4] b) Die Tangente im hochpunkt H (1|4) begrenzt mit dem graphen von f ein Flächenstück. Ermitteln sie die maßzahl dieser Fläche c) der graph der funktion f schließt mit dem graphen der funktion g mit der gleichung g(x)=x^3-3x+1 zwei flächenstücke ein. Bestimmen sie den Inhalt der gesamtfläche d) Die fläche, die der graph von f mit der x-achse einschließt, soll durch eine vertikale gerade mit der gleichung x=t in zwei gleich große flächenstücke geteilt werden. bestimmen sie den parameter t

bei a) habe ich -30 rausbekommen, aber denke, dass das nicht richtig ist..

In der ersten Aufgabe verstehe ich nicht wie genau ich jetzt die gefärbte Fläche berechnen kann welche Grenzen ich bei dem integral angeben soll usw. und in Aufgabe 2 müsste ich doch erstmal den Grad der Funktion wissen um sie aufstellen zu können, nur woher weiß ich das?

ich schreibe morgen eine Matheklausur und muss die Ableitungsregeln können. Ich habe folgendes Problem: Ich weiß, die Aufgabe ist wohl das einfachste was es gibt, aber ich verstehe nicht wie man auf die Lösung kommt? Die Funktionen und dazu gehörige Ableitungen lauten: 1) f(x) = 2x * (4x + 1) -> f´(x) = 2* (4x + 1) + 2x * 4 2) f(x) = (2 -5x) * (x + 2) -> f´(x) = (-5) * (x + 2) + (2 - 5x) * 1 3) f(x) = 7x * e^(x^2 -1) -> f´(x) = 7* (e^(x^2 -1)) * 7x * 2x * e^(x^2 -1) Wie leitet man noch mal diese drei Funktionen ab? Kurze Erklärung reicht, danke schon mal!

Hallo, Ich habe hier eine Textaufgabe zur Integralrechnung. Es geht um einen Heißluftballon. Er startet zum Zeitpunkt 0 und landet nach 4 Stunden. Die Funktion ist f(x)= 0.1x^3 - 0.65x^2 + 6. X ist dabei die verstrichene Zeit seit dem Start in Stunden & f(x) ist die Steig-/Fallgeschwindigkeit in km/h.

Ich habe bereits alle anderen Teilaufgaben ohne Probleme gelöst, aber jetzt hänge ich fest.

Die Aufgabe ist: Welche maximale Höhe erreicht der Ballon?

Ein Ansatz würde mir schon reichen. Danke!

Icj bin gerade dabei für meine Matheklausur zu lernen, und bin dabei auf folgende Aufgabe gestoßen:

Manuel behauptet: "(Integral a bis x) f(t)dt kann keine Stammfunktion von f sein weil der Ausdruck zwei Variablen enthält." Dabei sind a,x und t reelle Zahlen, x und t sind variabel, a fest. Nehmen Sie Stellung zu Manuels Behauptung.

So ich verstehe nun weder Manuels Behauptung, noch wie ich bei der Aufgabe vorgehen muss. Die gegebene Funktion ist doch gar keine Stammfunktion sondern eine Integralfunktion??

Ich finde Integralrechnung eigentlich recht einfach, aber wenn dann solche Textaufgaben kommen, bin ich raus...

Ich würde mich über Hilfe sehr freuen!

.

Woher weiß ich welche Zahl im integral oben steht und welche unten?

Hallo Leute, bei Textaufgaben in Mathe fällt es mir manchmal besonders schwer herauszufiltern nach was ich genau suchen muss! Kennt ihr einige typische Wörter/Sätze an denen man das erkennt? Beispiel: "Steilster Anstieg", "Steilster Abfall" oder eine "Änderung der Krümmung" stehen für einen Wendepunkt. Aber was ist mit anderen Kriterien?

Ich sage schon mal Dankeschön und wünsche euch noch einen schönen Freitag :-)

Hallo liebe Leute,

ich bin jetzt aus Verzweiflung hier gelandet. Ich kam eigentlich immer relativ gut zurecht, aber jetzt kommen aufgeben wo ich nicht weiter weis.

1.Eine ganzrationale Funktion 4. Grades schneidet die X-Achse bei x=4 und hat im Ursrpung einen Wendepunkt mit waagerechter Tangente. Sie schließt mit der X-Achse im 1. Quadranten eine Fläche von 6,4 F.E. ein. Wie lautet die Funktion ?

2.Eine achsensymmetrische Parabell verläuft durch A(0/0) und B(1/1). Eine andere achsensymmetrische Parabell geht durch C(1/2) und D(4/0). Berechne die Fläche, die von den beiden Parabelln so wie den Strecken BC und AD begrenzt wird.

Ich wäre euch sehr dankbar, wenn ihr mir evtl. sagen könntet wie ich an die Aufgaben rangehen soll. Wo ich das nachlesen kann oder welche Themen das genau sind. Ich suche seit einer Stunde aber kann kaum was finden, hab hier bisschen was versucht, aber kriege es nicht hin. Danke!

mfG Patrick :-)

Hallo,

Ich habe ein Problem bei einer Übungsaufgabe bzw. komme nicht weiter.

Die Aufgabe lautet: Integral von x sqrt(x-2) dx
Außerdem ist Substitution mit u²=x-2 vorgegeben.

Klappt soweit auch alles wunderbar. Nur wenn ich das dx ersetze habe ich dort wieder ein x stehen (in der Ableitung von u (also sqrt(x-2)d/dx)).
Und ab dem Punkt komme ich nicht weiter.

Darf ich das dann gleich nochmal substituieren?
Bin für jede Hilfe und jeden Zaunpfahl dankbar.

PS: Hier der Link zur Aufgabe in WA: http://www.wolframalpha.com/input/?i=integrate%3Axsqrt%28x-2%29

Und ein Bild hänge ich auch noch an.

Hi an alle mathepofis!
morgen schreibe ich eine Klausur über Integralrechnung. allerdings weiß ich nicht genau, was die Aufleitung des Bruchs ist.
ich hoffe, jemand kann mir helfen.

Danke!

Hallo Leute ich Sitze hier und verzweifle an einer Teilaufgabe :( Ich habe ein Fischlogo und habe jetzt schon die Funktion sogleich ungern bestimmt. f(x)=(-1/8x^2)+2 g(x)=(3/16x^2)-3 An der höchsten stelle ist der Fisch 5dm hoch und ist 8dm breit der Fisch liegt in der Mitte der Koordinatensystems also liegt er 4dm im links und 4dm im rechts von der y Achse. Und 2dm über und 3dm unter der x Achse. Nun soll ich den Intervall angeben von wo bis wo das Logo mindestens 2,5 DM hoch ist. Bitte helft mir 😦

Sind die Integralrechnung und die Differentialrechnung quasi Unterpunkte der Kurvendiskussion?

Oder inwiefern unterscheiden sich Kurvendiskussion und Differentialrechnung?

Wir haben in der Schule (Kl. 11) gerade die Integralrechnung. Wir haben gelernt, dass man sich bei dem Annäherungsverfahren der orientierten Flächeninhalte bei Ober- und Untersumme bei der Obersumme immer an den größten und bei der Untersumme immer an den kleinsten Funktionswerten im Intervall orientiert. Jetzt liegt der Graph unter der x-Achse, sodass man bei der Orientierung an den größten Funktionswerten natürlich den kleinsten Flächeninhalt herausbekommt. Der orientierte Flächeninhalt ist aber ja der kleinste, da er negativ ist. Ist das was ich da einzeichne und ausrechne jetzt Ober- oder Untersumme? Das versteh ich irgendwie nicht... Achja.. die Funktion ist monoton steigend... Wenn mir jmd helfen könnte, wäre ich sehr dankbar... LG

Hallo,

ich werde eine Facharbeit in dem Fach Mathe (Klasse 11, Gymnasium) schreiben und das Thema soll in Richtung Integralrechnung gehen. Die Facharbeit soll ungefähr 20 Seiten lang sein. Nun zu meiner Frage, Integralrechnung hatten wir noch gar nicht als Thema in Mathe, aber ich weiß grob, dass es um die Zusammenhänge zwischen Funktionen und Flächen geht.

Welches Unterthema der Integralrechnung würdet ihr mir für meine Facharbeit vorschlagen?

Eine weitere Voraussetzung ist ein eigenes Beispiel: Wäre mein Thema z.B. Volumenberechnung so müsste ich als Beispiel die Volumenberechnung eines persönlichen Gebäudes wie z.B. meinem Haus nehmen.

Ich brauche also ein Thema im Bereich Integralrechnung, worüber ich 20 Seiten schreiben kann und ein eigenes Beispiel einfügen kann.

Ich freue mich über eure Vorschläge und bedanke mich vorab :-)

Hallo Leute, ich bräuchte Hilfe bei einer Mathehausaufgabe. Gegeben ist: f(x)= -4/3*x^3+bx+4. Gesucht ist die Stammfunktion F(x) welche durch die beiden Punkte P(3/-7) und Q(1/11:3). Ich weis aufjedenfall, dass ich integrieren muss, also F(x) bilden muss. Das wäre dann schonmal: F(x)= -4/12x^4+b/2x^2+4x+c. Nur weis ich jetzt nicht was ich mit den beiden Punkten machen soll. Wärs einer dann einfach einsetzen, aber mit 2 Punkten haben wir noch nichts gerechnet. Die Differenz der beiden Punkte bilden geht jaa irgendwie auch nicht. Vielleicht 2 mal die Funktion für jeweils die Punkte einsetzen?

Danke für eventuelle Antworten:)

Wie kann man C bei einer Stammfunktion bestimmen? David

Was bedeutet eine Zahl vor der kuriosen "Klammer" der angegebenen Intergrationsgrenzen? Und wie geht man damit um? Muss man die beachten?

(...) - 10 (Integral von 3,3 bis -1) 1/2x^2dx

hallo,

wie funktioniert das sog. ,,Kästchen zählen'' ? wenn man den flächeninhalt z.B. in einer parabel bestimmt muss man sie doch zuerst aufteilen oder? ich verstehe das nicht ganz..

Vielen Dank im Voraus!!

lg bibi

Ich habe das Thema Integralrechnung und will die Fläche zwischen zwei Graphen errechnen. Dazu muss ich wissen welcher Graph von zweien der Größere ist. Wie stelle ich das fest? Zum Beispiel bei den beiden Graphen

f(x)= 1 / x^2 - 0,25 und g(x)= -16 * x + 11,5

?

Sodass ich am Ende entweder sagen kann f(x) ist größergleich g(x) oder f(x) ist kleinergleich g(x) .

Hallo Liebe Community, ich habe zwei Matheaufgaben gerechnet, bei denen bei mir allerdings nicht das herauskommt, was herauskommen soll. Leider entdecke ich aber keinen Fehler. Wenn ihr einen Fehler finden könntet wäre das toll.

Das Profil einer Skateboardrampe wird von zwei quadratischen Parabeln f und g gebildet, die über einen senkrechten Absatz miteinander verbunden sind. Welche Querschnittsfläche hat die Rampe?

Die Gleichungen lauten f(x) = 1/6x^2 + x + 3/2 und g(x) = 1/8x^2 - x + 2. Ich habe nun jeweils das Integral von -3 bis 0 (f(x)) und 0 und 4 (g(x)) (so lang ist die Skateboardrampe) berechnet, für f(x) kommt 9/8 heraus und für g(x) 8/3. Addiert man dies nun kommt man auf 3,79m^2, herauskommen soll aber 4,17m^2.

Ein Pavillon besitzt eine Glasfront, die oben von einer sichelförmigen Holzrahmung abgeschlossen wird. Das Holz ist 20 cm dick. Was wiegt die Rahmung? (Dichte Holz: 0,7 g/cm^3)

Hier lauten die Gleichungen -5/36x^2+5 und -16/121x^2+4. Nun habe ich das Integral von -6 bis 6 ausgerechnet (so lang ist der Pavillon; höchster Punkt auf der y-Achse) für (f(x)-g(x)=h(x)) und das mal 20*0,7=14, doch auch hier kommt mit -154,6 das falsche Ergebnis heraus. Richtig wäre in diesem Fall 10,67 (Einheit weiß ich nicht).

Ich hoffe ihr könnt mir helfen (und das die Frage nicht gelöscht wird)

Mit freundlichen Grüßen

Feuermond16

Die Aufgabe lautet : bestimmen sie K So,dass der Graph der Funktion f mit der X-Achse eine Fläche vom angegebenen Flächeninhalt A einschließt . f(x) = x^2 - kx A = 36 Also ich erwarte jz keine komplette Lösung, würde nur mal gerne wissen wie ich vorgehen sollte und was ich genau zu tun habe. Am besten auch gleich die Stammfunktion von kx nennen... Denn da steh ich echt aufn Schlauch..... Vielen dank im vorraus

Bei der Flächenberechnung eines bestimmten Integrals muss man die Betragsstriche schon von Anfang an setzen?

Beispiel: Integral von (2x+3)dx Obergrenze 4, Untergrenze -1

Bei F(4)-F(-1) = 28-(-2)=30 " " = I 28-(-2) I = 26

Was stimmt denn jetzt und warum?

Vielleicht könnte einer von euch mir hier weiterhelfen?! Und bitte nur eine erklären, damit ich mich an die weiteren wagen kann. Vielen lieben Dank!!!

Ich hab mir seit gestern Abend den Kopf zerbrochen, welche Regeln man dabei anwenden muss, um auf [ 2 * Wurzel x ] zu kommen.

Mit der Anwendung der mathematischen Prinzipien, die mir bekannt sind, komme ich auf...

                    (aufleiten)

[1/Wurzel x] = (Wurzel x)^-1 ----------------------> (1/-1+1) * (Wurzel x)^0 = 1/0 * 1 = 1/0

Ganz davon abgesehen, dass diese Lösung unzulässig ist, weil man ja nicht durch Null teilen darf, lautet die richtige Stammfunktion laut Online-Rechner [ 2 * Wurzel x ]

Aber wie kommt man denn darauf? Ich hab schon die Mathe-Spezial-Super online-Foren durchwühlt, aber leider noch keine nachvollziehbare Erklärung finden können...

Und NEIN, ich werde mir nicht 10 Stunden lang einen Account in einem solchen Forum zulegen, nur um 1 Frage zu stellen ;)

Danke chucknils

Hi Leute..

ich habe ein riesiges Problem. Ich soll eine Präsentation bzw. Ausarbeitung zum Thema Integralrechnung anfertigen. Das Problem : Ich weiß noch nicht einmal wie ich ein Koordinatensystem in Word bekommen geschweige denn die Funktion selber so zu gestalten wie ich es vorhabe (mit Farbe etc.) kann mir irgend jemand helfen? oder weiß jemand ein gutes Programm mit dem ich einfach Formeln bzw eine Funktion + Koordinatensystem erstellen kann und diese anschließend in Word einfügen kann!! Bitte helft mir!

Danke!

Hallo, ich habe ein Problem: Und zwar sitze ich über meinen Mathe-Hausaufgaben. Einen Großteil habe ich ein Glück schon hinter mir :)

Nur muss ich jetzt angeben, wie a gewählt werden muss,damit die markierte Fläche den angegebenen Inhalt hat. ?

Ich weiß überhaupt nicht, wie ich daurauf kommen soll?

Ein Beispiel wäre z.B. f(x)=3x^2+a^2 A= 21 Das Integral geht von -1 bis 2

Ich habe leider noch nicht einmal einen Ansatz, habe auch schon verschiedenes ausprobiert, kam immer zu unterschiedlichen Ergebnissen. Für Hilfe wäre ich sehr dankbar.

LG Starli

Hallo, habe ein echtes Verständnisproblem bei b) und c) folgender Aufgabe:

Ein Tomatensetzling besitzt beim Einpflanzen eine Höhe von 5 cm. Seine Höhe nimmt mit der Geschwindigkeit v(t)=−0,1t³+t² zu. (t in Wochen, v in cm/ Woche). Rekonstruiere die Funktion h, die die Höhe der Pflanze erfasst. Kläre folgende Fragen:

a) Wie lange dauert die Wachstumsphase? b) Wie hoch wird die Pflanze maximal? c) Wie hoch wird die Pflanze zum Zeitpunkt des schnellsten Wachstums sein.

also h(t)= − 0,4 t hoch 4 + t³/3 + 5 (Stammfunktion)

a) da habe ich die Geschwindigkeitsfunktion v(t) gleich 0 gesetzt und t1=0 und t2=10 herausbekommen. die Antwort wäre also nach 10 Wochen.

b) hier kommt nun mein erstes Problem: Wenn ich 10 in die Höhenfunktion (h(t)) einsetze und die Höhe berechne, erhält ich eine negative Höhe???? Wo liegt bitte der Denkfehler h(t) = - 4000 + 1000/3 + 5

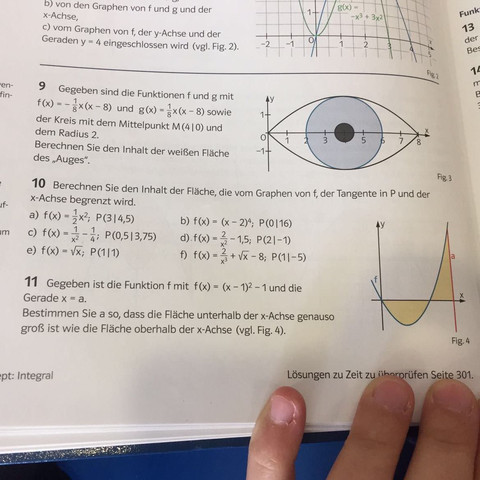
c) die Ableitung der Geschwindigkeitsfunktion nehmen (v′(t)) und die Werte in die Höhenfunktion einsetzen (h(t)). v ' (t) = -0,3 t² + 2t Setze dies nun gleich Null und erhalte: t1 = 0, t2 = 20/3 dies beide Werte wurde ich dann in h(t) einsetzen, aber wieso?

Bin für jede sinnvolle Hilfe dankbar, bitte keine Kommentare, wie: Mache deine Aufgaben allein oder so, dass bringt mich nicht weiter..... ganz vielen dank im voraus und natürlich verteile ich zum Schluss auch das Sternchen, denn das ist nur fair bei toller HIlfe :)

Hi

Eine kurze Frage: Ab wann, muss ich beim Integrieren die Kostante c beachten. Ich komme immer durcheinander. Mal soll der Flächeninhalt z.B. zw. Graph und x-Achse berechnet werden und die gegebene Funktion f wird dazu einfach nur integriert (ohne c zu berücksichtigen. Ein anderes Mal geschieht das Gleiche, aber c wird mit eingebracht.

Woran erkenne ich das c berücksichtigt werden muss bzw. wann bringe ich c mit ein?

Danke an alle!

Wann muss ich bei der Integralrechnung Betragstriche setzen und woran merke ich dass???

Was ist die Stammfunktion von 1/4 x^2 ?? (x^2 außerhalb des Bruches)

Hier komm ich bei der Inegralrechnung einfach nicht weiter. WIe findet man die Stammfunktion heraus, wenn das x außerhalb des Bruches steht?

Hallo Leute,

Ich wollte ein paar Aufgaben rechnen , da wir das Thema grade in der Schule haben und dabei bin ich auf ein Problem gestoßen. Es geht um folgende Aufgabe:

Berechnen Sie Un und On für die Funktion f über dem Intervall I.

Die Funktion lautet: f(x) = x + 1, I= [0:1]

Benötigte Summenformel: 1 + 2 + .... + n = (n(n+1))/2

Ich habe schonmal angefangen, komme aber nich auf den vorderern Teil der Summenformel:

On = 1/n * [((1/n)+1) + ((2/n)+1)..... + (n/n)+1]

Dann habe ich (1/n) ausgeklammert:

On = 1/n² * [(1+n) + (2+n) + ..... + (n+n)]

Kann mir jemand sagen wo mein Fehler liegt, oder wie ich nun weiter machen muss?

GLG

siehe Frage,

PS: Danke schonmal für die Antworten

Hallo, ich möchte gern wissen was ich beachten muss, wenn ich beispielsweise eine Gleichung integrieren muss mit einer Klammer im Gegensatz zu keiner Klammer?

Ein Beispiel:

ohne Klammer:

∫ 5x + 5 dx ------> intergiert heißt es 2,5 x² + 5x + C

mit Klammer:

∫ (5x + 5) dx -----> muss ich da jetzt irgendwas beachten. ich würde jetzt ganz einfach so integrieren wie bei ohne Klammer?

Danke. LG Synapse22

halli hallo ich bräucht grad mal hilfe.

unzwar lernen wir gerade das "aufleiten" als gegensatz zum ableiten. geht auch bis jetzt ohne probleme, nur hakt es bei einer kleinen funktion:       f(x) = (2 - x)²

wie leite ich die auf? muss ich da die kettenregel andersrum anwenden?! aber wie? o.O

die beste nachvollziehbare antwort kriegt natürlich die 25 punkte :)

Tach zusammen. Wir haben heute im Unterricht mit der Rotation von Körpern begonnen. Jetzt haben wir folgende Hausaufgabe aufbekommen:

Durch Rotation des Graphen von f mit f(x) = Wurzel x um die x-Achse entsteht ein (liegendes) Gefäß. Dieses Gefäß wird aufgestellt und mit einer Flüssigkeit gefüllt. Bis zu welcher Höhe steht die Flüssigkeit in dem Gefäß, wenn ihr Volumen 30 beträgt?

Wäre Euch dankbar wenn mir das jemand vorrechnern und/oder erklären könnte. Danke schonmal =)