Integralrechnung, a?
Hallo :-) Wie gehe ich die Aufgabe 11 an?
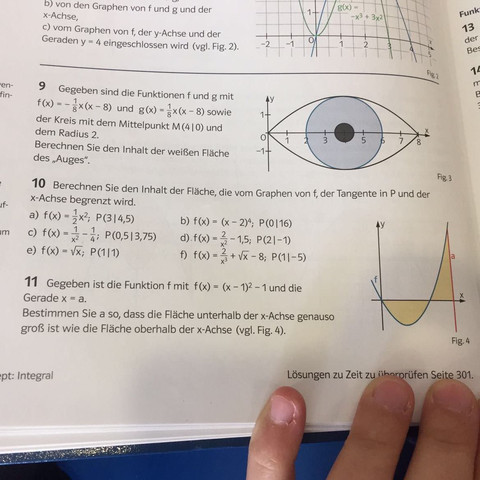
3 Antworten
f(x) = (x - 1) ^ 2 - 1
Zweite binomische Formel anwenden -->
f(x) = x ^ 2 - 2 * x
Nullstellen von f(x) bestimmen -->
x ^ 2 - 2 * x = 0
x * (x - 2) = 0
Weil du x bzw. x ^ 1 ausklammern konntest ist eine Nullstelle bei x _ 1 = 0
x _ 1 = 0
x - 2 = 0 | + 2
x _ 2 = 2
Nun berechnest du die Stammfunktion von f(x)
f(x) = x ^ 2 - 2 * x
F(x) = (1 / 3) * x ^ 3 - x ^ 2 + C (Stammfunktion)
Nun berechnest du den Flächeninhalt von 0 bis 2
Erstmal wird C = 0 gesetzt, das darf man immer machen.
( (1 / 3) * 2 ^ 3 - 2 ^ 2) - ( (1 / 3) * 0 ^ 3 - 0 ^ 2) = - 4 / 3
Auf das Minuszeichen kann verzichtet werden, weil das Minuszeichen nur anzeigt, dass sich die Fläche unterhalb der x-Achse befindet.
Der Flächeninhalt, der zwischen der Funktion f(x) = (x - 1) ^ 2 - 1 und der x - Achse zwischen x = 0 und x = 2 eingeschlossen ist, beträgt also 4 / 3
Nun soll folgendes gelten -->
((1 / 3) * a ^ 3 - a ^ 2) - ((1 / 3) * 2 ^ 3 - 2 ^ 2) = 4 / 3
Das kann man vereinfachen -->
(1 / 3) * a ^ 3 - a ^ 2 + 4 / 3 = 4 / 3 | - 4 / 3
(1 / 3) * a ^ 3 - a ^ 2 = 0
Man kann a ^ 2 ausklammern -->
a ^ 2 * ((1 / 3) * a - 1) = 0
a ^ 2 kann man ignorieren, weil das a _ 1 = 0 und a _ 2 = 0 ergibt, was kleiner als 2 ist, und somit nicht sein darf.
Übrig bleibt -->
(1 / 3) * a - 1 = 0 | + 1
(1 / 3) * a = 1 | * 3
a = 3
Das ist dein Endergebnis !!
Der ABSOLUTE (ohne Beachtung des Vorzeichens !!!) Flächeninhalt zwischen 0 und 2 ist genauso groß wie der Flächeninhalt zwischen 2 und 3.
Tipp: Berechne erst die Fläche links unten, dann berechne die Fläche rechts oben in Abhängigkeit von a (Frage an dich: Wie geht a in die Berechnung der zweiten Fläche ein?). Dann setze die Flächen gleich und bestimme aus der so entstehenden Gleichung a.
- Integral zwischen 0 und 2 berechnen. Das ist dann die untere Fläche.
- Integral zwischen 2 und allgemein a berechnen und dann mit der eben berechneten Fläche unterhalb gleichsetzen und nach a auflösen.