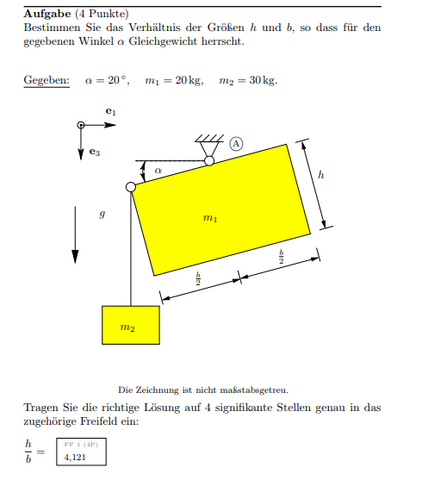
Wahrscheinlichster Abstand eines elektrons von Kern beim Wasserstoffatom berechnen?
Hallo. Ich habe mir gerade die Berechnung angeschaut und habe ein paar Punkte gefunden die ich nicht verstehe.
Bei dem wahrscheinlichsten Abstand ist die Ableitung der Wahrscheinlichkeitsfunktion gleich 0
dW/dr=0
dw ist definiert als
dw = ψ*ψdv = ψ*ψ dφ sin(θ) dθ r² dr
Hier wir dann angegeben dass
dφ sin(θ) dθ = 4π
wenn die Funktion ψ nicht von teta und phi abhängt. Das ergibt in meinen Augen keinen Sinn. Es gilt
∫(0 bis pi) ∫(0 bis 2pi) dφ sin(θ) dθ r² dr = 4π
Aber da das nur beim Integrieren über den Gesamten Bereich gilt ergibt es keinen Sinn, dass es ohne Integral auch 4π ist.
Selbst wenn das der Fall ist haben wir dann immernoch
dW/dr = (ψ*ψ 4π r² dr)/dr
Beim Ableiten wird dann das dr im oberen Term wiederum einfach ignoriert und nur ψ*ψ r² abgeleitet.
dW/dr = d/dr(r² ψ*ψ)
Kann mir jemand erklären was das soll?