Wahrscheinlichster Abstand eines elektrons von Kern beim Wasserstoffatom berechnen?
Hallo. Ich habe mir gerade die Berechnung angeschaut und habe ein paar Punkte gefunden die ich nicht verstehe.
Bei dem wahrscheinlichsten Abstand ist die Ableitung der Wahrscheinlichkeitsfunktion gleich 0
dW/dr=0
dw ist definiert als
dw = ψ*ψdv = ψ*ψ dφ sin(θ) dθ r² dr
Hier wir dann angegeben dass
dφ sin(θ) dθ = 4π
wenn die Funktion ψ nicht von teta und phi abhängt. Das ergibt in meinen Augen keinen Sinn. Es gilt
∫(0 bis pi) ∫(0 bis 2pi) dφ sin(θ) dθ r² dr = 4π
Aber da das nur beim Integrieren über den Gesamten Bereich gilt ergibt es keinen Sinn, dass es ohne Integral auch 4π ist.
Selbst wenn das der Fall ist haben wir dann immernoch
dW/dr = (ψ*ψ 4π r² dr)/dr
Beim Ableiten wird dann das dr im oberen Term wiederum einfach ignoriert und nur ψ*ψ r² abgeleitet.
dW/dr = d/dr(r² ψ*ψ)
Kann mir jemand erklären was das soll?
2 Antworten
Es ist so schwer zu lesen, daß ich es mir nicht antun will. Stattdessen rechne ich es selber durch. Ich nehme an, daß sich das Elektron im 1s-Orbital aufhält, die zugehörige Wellenfunktion ist ψₛ₌₀(r)=e⁻ʳ (wenn man atomaren Einheiten verwendet, also r in Vielfachen des Bohr-Radius mißt), den Normierungsfaktor 1/√π können wir weglassen, weil der die Lage des Maximums nicht beeinflußt.
Die Wahrscheinlichkeit, das Elektron in einem Abstand zwischen r und r+dr anzutreffen, ist aber nicht einfach ψ², sondern man muß eine dünne Kugelschale mit Radius r und Dicke dr betrachten; deren Volumen ist 4πr²⋅dr (Oberfläche⋅Dicke, weil man eine dünne Kugelschale wie ein Prisma behandeln kann), also lautet die gesuchte Wahrscheinlichkeitsdichte P(r)=r²⋅e⁻²ʳ. Dabei habe ich die 4π rausgekickt, weil wir ja nur das Maximum suchen und bereits das ψ unnormiert war, also summieren sich die Wahrscheinlichkeiten sowieso nie auf 1.
Beim groben Blicken auf Deine Frage komme ich zum Schluß, daß Du denselben Vorfaktor durch Integration über θ und φ erhalten hast. P(r)=∫∫ψ(r) r² sin(θ) dφ dθ, da kommt von der Integration übers φ ein Faktor 2π und von der übers θ ein Faktor 2, und damit haben wir es. Wichtig ist eh nur das r² (das kommt aus der Umrechung des Volumselementes dx dy dz = r² sin(θ) dr dφ dθ von kartesischen Koordinaten in Polarkoordinaten, weil wir das ψ ja in Polarkoordinaten haben).
Und jetzt wollen wir noch schnell das Maximum von P(r)=r²⋅e⁻²ʳ berechnen. Dazu brauchen wir die erste Ableitung P’(r)=2r⋅e⁻²ʳ + r²⋅(−2)⋅e⁻²ʳ=2(r−r²)⋅e⁻²ʳ, und da die Exponentialfunktion niemals durch Null geht, kann eine Nullstelle nur aus dem Polynom r−r²=r⋅(1−r) rauskommen, also bei r=0 (unphysikalisch) und r=1 (richtige Lösung).
Ich habe mit hilfe der Zeichen die du verwendet hast die Frage überarbeitet. es müsste jetzt leserlicher sein
∫(0 bis pi) ∫(0 bis 2pi) dφ sin(θ) dθ r² dr = 4π
Das Problem liegt wohl hier. Da müssen wir ein bißchen weiter ausholen.
Die Wellenfunktion ψ(x,y,z) ist eine Funktion des Raumes, ordnet also jedem Raumpunkt einen Funktionswert zu. Ihr Quadrat ist eine Wahrscheinlichkeitsdichte, also steht ψ²(x,y,z) schlampig gesagt für die Wahrscheinlichkeits, das Elektron am Punkt x,y,z zu finden; das ist schlampig, weil ein Punkt unendlich klein ist und das Elektron daher niemals genau dort sein kann. Die besere Formulierung ist daß ψ²(x,y,z) dx dy dz die Wahrscheinlichkeit dafür ist, daß das Elektron in einem Würfelchen mit der Kantenlänge dx,dy,dz am Punkt x,y,z steckt. Damit haben wir den ∞ kleinen Punkt durch ein infinitesimal kleines Volumen ersetzt, das ist sauberer.
Wollen wir ein endliches Volumen, dann müssen wir integrieren, und zwar über ein endliches Volumen dV = dx dy dz.
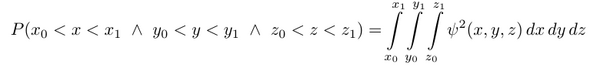
Das Integral berechnet die Wahrscheinlichkeit, daß die x-Koordinate des Elektrons zwischen x₀ und x₁ liegt etc, beschreibt also einen endlich großen Würfel bzw. Quader. Die Wahl der Würfelform kommt daher, daß wir in kartesischen Koordinaten operieren, und da ist die Figur, die durch die Koordinatenebenen (z.B. x=x₀ beschreibt eine Ebene parallel zu xy und xz) begrenzt wird, eben automatisch würfelig.
Jetzt wollen wir aber eine radiale Aufenthaltswahrscheinlichkeit berechnen (mit welcher Wahrscheinlichkeit ist das Ding wie weit vom Kern weg). Dafür eignen sich Polarkoordinaten besser, weil dort r=r₀ eine Kugeloberfläche beschreibt. Außerdem wollen wir die r-Koordinate offen lassen und nur über φ und θ integrieren, damit wir uns das nachher für beliebige r-Werte ansehen können. Auf diese Art werden wir die Koordinaten φ und θ los, für die wir uns eh nicht interessieren und von der die Wellenfunktion gar nicht abhängt. Die Wellenfunktion ψ=e⁻ʳ haben wir bereits in Polarkoordinaten gegeben, passt also.
Stellt sich noch die Frage, wie das Volumselement dV in Polarkoordinaten aussieht; der naïve Verdacht dr dφ dθ kann es bestimmt nicht sein, das stimmt ja nicht mal einheitenmäßig. Richtig ist dV = r² sin(θ) dr dφ dθ, das kann man mit etwas Geschick geometrisch ableiten, oder formaler über die Jacobi-Determinante. Wir integrieren nur über φ und θ und bekommen:
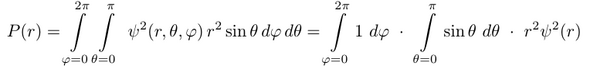
Dabei habe ich ausgenützt, daß ψ nicht von θ und φ abhängt und daß man die beiden Integrale von ψ loslösen kann. Das φ-Integral liefert trivialerweise 2π und das θ-Integral ist −cos(π)+cos(0)=2. Damit erhalten wir P(r)=4π⋅r²⋅ψ²(r), und ich glaube, das war Deine Frage.
Damit ist auch klar, warum die Gleichung dφ sin(θ) dθ = 4π so komisch aussieht, richtig wäre ∫∫dφ sin(θ) dθ = 4π wenn man über den ganzen Gültigkeitsbereich der Variablen φ und θ integriert. Warum man das macht habe ich glaube ich ausführlich erklärt.
In Deinen letzten drei Zeilen spüre ich noch eine Konfusion mit dem dr. In meiner Ableitung ist kein dr vorgekommen, aus dem simplen Grund, daß wir nie über r integriert haben: Wenn man über eine Variable integriert, dann ist sie weg, und unser P(r) soll ja von r abhängen. P(r) ist eine Wahrscheinlichkeitsdichte für die radiale Aufenthaltswahrscheinlichkeit, also ist die Wahrscheinlichkeit, das Elektron zwischen den Abständen r und r+dr zu treffen, genau P(r).
Die Wellenfunktion für das 1s-Orbital im Wasserstoff ist e⁻ʳ/√π, und daher ist P(r)=4r²e⁻²ʳ, dabei hat sich das 1/√π aus dem Normierungsfaktor der Funktion mit dem π aus der Winkelintegration rausgekürzt. Diese Funktion können wir jetzt z.B. benützen, um auszurechnen, wie wahrscheinlich es ist, daß das Elektron max. 1 bohr vom Kern entfernt aufhält, dazu summieren (≈integrieren) wir über alle Wahrscheinlichkeitswerte von r=0 bis r=1.
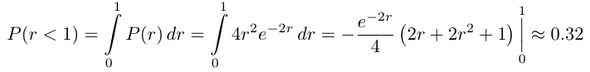
Du siehst, die Integration über r kommt erst ins Spiel, wenn wir wirklich Zahlen haben wollen (so wie im in der ersten Formel oben mit kartesischen Koordinaten, auch wenn ich dort keine Zahlen eingesetzt habe). Auf jeden Fall muß man dreimal integrieren, bis man eine Zahl bekommt; in der radialen Wahrscheinlichkeitsdichte sind zwei Integrationen schon ausgeführt, so daß man für die Anwendung nur noch eine weitere (die über dr) braucht.
(Da ich kein Integrationsweltmeister bin, habe ich die Formel aus dem Internet abgeschrieben und den Zahlenwert nicht durch Einsetzen, sondern durch numerische Integration bestimmt. Ich hoffe, es stimmt trotzdem).
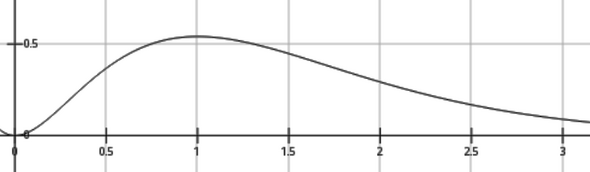
Du siehst auch, daß obwohl r=1 der häufigste Radius (Maximum der Wahrscheinlichkeitsdichte) ist, das Elektron nur 32% Aufenthaltswahrscheinlichkeit innerhalb dieses Radius hat. Das liegt natürlich daran, daß 4r²e⁻²ʳ sehr unsymmetrisch um sein Maximum ist:

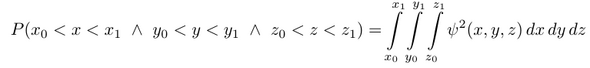
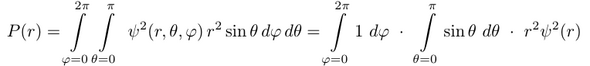
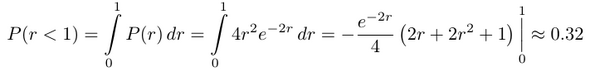
Teil der Frage war wie man mathematisch auf dV=4πr²⋅dr kommt, weil dass müsste ja heißen dass r² sin(θ) dφ dθ = 4πr²⋅dr wass ja aber nur bei der Integration zustande kommt. Da wir nicht integrieren verstehe ich den Sinn nicht.