Prisma - Abstand berechnen?
Die Brechzahl in einer bestimmten Glassorte beträgt für rotes Licht n = 1,51 und für blaues Licht n = 1,52. Auf ein Prisma, dessen Grundfläche ein gleichseitiges Dreieck ist, fällt ein schmales Lichtbündel mit einem Einfallswinkel von 45°. Das Licht wird auf einem 2 mm entfernten Schirm aufgefangen. Berechnen Sie den Abstand zwischen dem blauen und dem roten Bereich im Spektrum auf dem Schirm.
Einen Ansatz habe ich nicht wirklich..
Meine Idee wäre zunächst den "anderen" Winkel auszurechnen mit:
sin(alpha1) / sin(alpha2) = n_2/ n_1
Hab dann für alpha_2 = 44,63 Grad
Dann würde ich versuchen die Ausbreitungsgeschwindigkeit zu berechnen, aber hätte dann zwei Unbekannte, wenn gilt
sin(alpha1) / sin(alpha2) = c_1/ c_2
3 Antworten
1) Prüfe, ob der Schirm wirklich nur 2 mm entfernt sein soll
2) Fertige eine Zeichnung an.
3) Berechne die beiden Ausfallwinkel, zunächst an der ersten Glasfläche, dann an der zweiten Glasfläche. Den Einfallswinkel an der zweiten Glasfläche bekommst Du aus dem zuvor berechneten Ausfallwinkel plus dem Wissen, dass das dreieck ein gleichseitiges ist.
4) Gehe zur Vereinfachung davon aus, dass der Schirm, der rote und der blaue Lichtstrahl ein gleichschenkliges Dreieck bilden.
5) Zeichne die Winkelhalbierende der beiden Strahlen - jetzt hast Du zwei rechtwinklige Dreiecke, mit den beiden Strahlen als Hypotenusen.
Hätte eine Frage zur Berechnung der Winkel..
In einer Formel steht, dass sin(alpha1)/ sin(alpha2) gleich dem Quotient von n_1 und n_2 ist.. Wenn ich eine Brechzahl gegeben ist, dann ist die Brechzahl doch der Quotient aus n_1 und n_2 oder?
Ich hätte nämlich dann für alpha bei der ersten Brechung 27,92°
Ich verstehe noch nicht ganz wie man auf den zweiten WInkel kommt, es ist ja gleichseitig, aber ist es nicht willkürlich, wo es gebrochen wird?
> In einer Formel steht, dass sin(alpha1)/ sin(alpha2) gleich dem Quotient von n_1 und n_2 ist..
Korrekt. Und wenn man Formeln stur auswendigzulernen pflegt, anstatt sie zu verstehen, vergisst man leicht, was damit beschrieben wird: Die Brechung an einer Oberfläche für eine Wellenlänge, wobei die beiden Medien n1 und n2 als Brechzahl haben.
Ziemlich ungeeignet in Deinem Fall - denn dass Luft eine von 1 verschiedene Brechzahl hat, kann man getrost ignorieren, wenn die anderen Brechzahlen nur mit 3 Ziffern angegeben sind.
Du musst für beide Lichtstrahlen getrennt berechnen, unter welchem Winkel sie aus der zweiten Oberfläche austreten.
Es ist willkürlich - aber das ändert nichts am Austritts-Winkel. Jedenfalls solange nicht, wie das Licht aus derselben Prismafläche austritt.
Wenn Du mit der Berechnung für den von Dir gezeichneten Strahlenverlauf fertig bist, dann - und erst dann - ist es Zeit, zu prüfen, ob ein hinreichend weit verschobener Eintrittspunkt zu einem anderen Ergebnis führt.
Ich hoffe ich habe die Aufgabe noch heute gelöst :D
Zunächst fällt mal auf, was fehlt:
Die Größe des Primas nämlich.
Also ist es so klein, dass die Größe zu vernachlässigen ist.
Also kannst du die beiden Richtungsänderungen in eine zusammenfassen.
Dann rechnest du die Winkel einfach zusammen, den Ein->Ausfallswinkel und den Aus->Einfallswinkel. Oder umgekehrt.
Oder auch die beiden Richtungsänderungen.
Und die natürlich getrennt für die beiden Wellenlängen samt Brechzahlen.
Mit der Geschwindigkeit hat das nichts zu tun, außer im innersten physikalischen Kern, da ist sie der Grund für die Lichtbrechung.
Ich weiß nicht was das Wissen bringen soll, dass es ein gleichseitiges Dreieck ist.. Ich hab versucht den Winkel zu verschieben, aber ich sehe nichts
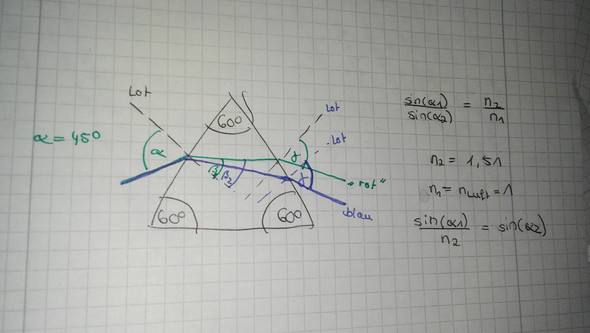
Die Zeichnung geht ja so gerade eben (ist Dir nicht aufgefallen, dass die beiden Lote parallel sein müssten?) aber die Beschriftung ist besch...
An der rechten Fläche sind zwei verschiedene Winkel beide mit alpha beschriftet, und zwei weitere überhaupt nicht. Und links heißt noch einer alpha, und alle drei alphas haben unterschiedliche Werte.
Und dann steht da noch eine Gleichung, die alpha1 und alpha2 verknüpft - aber nicht zu Deiner Zeichnung passt, denn dort heißen die Winkel alpha und beta.
Berechne bitte zuerst beta1 und beta2. Dann die beiden unbeschrifteten Winkel auf der anderen Glasfläche - genau dafür brauchst Du das Wissen um die Gleichseitigkeit bzw. den Prismawinkel von 60°.
Aus denen dann die beiden rechten alphas.
Verschieben sollst Du überhaupt nichts, zumindest nicht, bevor Du nicht die Aufgabe gelöst hast.
Davon abgesehen: Ich bleibe bei meiner Vermutung, dass Du Probleme mit Mathe hast, zumindest mit der Anwendung derselben. Denn die Aufgabe ist, sobald man die Zeichnung und den Zusammenhang zwischen Ein- und Ausfallswinkel hat, eine reine Mathe-Aufgabe.
Und ich bleibe bei meiner Empfehlung: Such' Dir einen Nachhilfelehrer für einmal die Woche, der Dir an den Stellen auf die Sprünge hilft, an denen sich aus der Ferne nicht sagen lässt, wo genau denn jetzt Dein Problem liegt.
Wie gesagt, ich weiß nicht wie ich beta berechnen soll.. Ja die sollen parallel sein, ist halt eine Freihandskizze
Ach ja es sollten nicht drei alphas sein, sondern ein alpha und einmal gamma_1 und gamma_2 ( habe die Beschriftung vergessen, ich weiß )
Kann ich es so rechnen (weiß halt nicht was ich mit dem gleichseitigen Dreieck machen soll):
sin(beta)/sin(gamma_1) = n_1/n_2
n_1 = 1 (Luft)
n_2 = 1,51 (Glas)
beta hatte ich ja ca. 28° raus .. falls es richtig ist
So ich glaube ich sehe es langsam... "verschieben" muss man schon ein bisschen:
Der Brechungswinkel und derWinkel gegenüber gamma bilden ein Dreieck. Der dritte Winkel ist 180°- 60°
Dadurch habe ich (so nenne ich es mal) delta.. Delta ist der "Einfallswinkel" und gamma der Ausfallswinkel. Jetzt die obere Formel anwenden nur, dass statt beta ein gamma steht.
Frage am Rande: Darf ich das Brechungsgesetz auch anwenden, wenn das Licht von einem dichteren Material in ein weniger dichteres Material geht?
Ich denke, jetzt hast Du es gerafft.
Natürlich gilt das Brechungsgesetz auch in diesem Fall. Der Lichtweg ist bekanntlich umkehrbar.
Zur Kontrolle: Vom dichteren ins dünnere Medium wird der Strahl vom Lot weg gebrochen.
Danke, aber das hat man echt nicht auf Anhieb gesehen.. Und wurde echt bei dem Beitrag runtergemacht weil ich was nicht verstehe (du jetzt nicht so sehr).. Man ist nicht dumm, wenn man was nicht versteht
Das ist sogar mir duchgeflutscht.