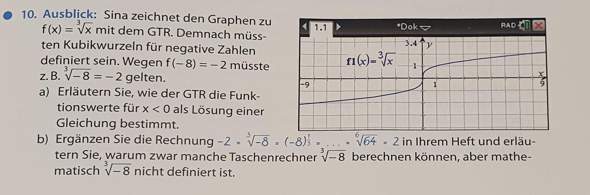
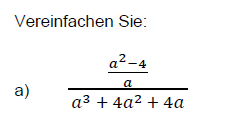
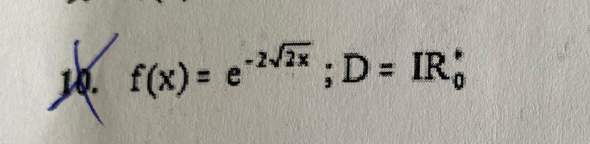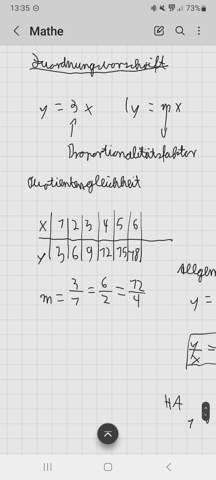Ist das einfach Term zusammenfassen oder was anderes?
Zusammenhang, es geht hier darum, dass man Messwerte geplottet hat und eine Ausgleichsgerade finden will, die möglichst wenig Fehler hat. Das, was anscheinend aus dieser Rechnung gefolgert wird, also der nächste Schritt, ist, von jedem Wert ein Quadrat zur Gerade hinzutun und die Gerade so ausrichtet, dass die summe der Quadrate minimal ist.
Also ich verstehe irgendwie den Zusammenhang zur Rechnung ist, auch nicht, was "Minimieren" ist. MOMENT. Da steht, durch Wahl von m und b. Heißt das dann, das man m und b so einsetzt, dass der Gesamtwert minimal ist? Bedeutet das minimieren?
Okay, m und b gehören zur Gerade=mx+b, aber was ist xi und yi? Also jetzt begreife ich, dass die Rechnung tatsächlich die Summe der Quadrate meint, und... Ist das die Varianz, weil ein kleiner Wert eine genauere Gerade bedeutet? und warum x I? Ist das der x und y Wert der Punkte? Oder der Gerade?