Algebra – die neusten Beiträge

Hallo Zusammen

Ich habe seit ca. 8 Jahren denselben Taschenrechner und zwar den heiss geliebten: Texas Instruments TI-30 eco RS.

Habe nun eine Hochfachschule als Technikerin (Fachrichtung Elektrotechnik) angefangen und fange nun an zu zweifeln dass mich dieser Taschenrechner ohne Probleme durch mein Studium bringen wird......

Nun ist die Frage: ist es nötig einen neuen zu kaufen (können die wirklich mehr)??
Wenn ja: was für einen würdet Ihr/Du empfehlen?

ACHTUNG: er MUSS ein "Wissenschaftlicher" Taschenrechner sein der NICHT algebrafähig ist: (d.h. ohne CAS) und NICHT programmierbar ist.

Mein momentaner Favorit ist: Casio FX991ES Plus
ABER hab keine Ahnung von ihm....

Ich danke :)

Habe versucht eine Gleichung für die n-te Ableitung einer Polynomfunktion herzuleiten und kam auf:

a mit kleingestellten n sollen die Koffizienten/Faktoren der Monomen/Glieder der Ausgangsfunktion sein.

Wäre super wenn mir das jemand nachprüfen und sagen könnte, ob und wo ich eine Gleichung dafür finde und ob ich einen groben Schnitzer begangen habe.

Würde mich freuen.

Hallo zusammen,

Die Scheitelform einer Normalparabel in der Mathematik lautet y=(x+p)²+q ? Woran erkenne ich jetzt wenn ob die Parabel nach oben oder nach unten geöffnet(also Negativ) ist? Und wie würde es heißen/aussehen wenn es eine nach unten geöffnete Parabel sein soll, ist das dann nur ein Minus vor der Klammer oder in der Klammer vor dem x ?

Ich hoffe ihr versteht was ich meine und würde mich auf schnelle Antworten freuen, ist nämlich sehr wichtig.

Danke ich voraus!

Ist jetzt nur ein Beispiel aber das kommt ziemlich oft als Lösung, kann mir jemand das eventuell erklären?

Wenn man sich im Modus für Matrizen befindet, ist es ja nicht möglich auch Hochzahlen einzugeben, und somit ein ewig langer Prozess die Grenzmatrix auszurechnen?

Weiß daher jemand wie man das sonst machen kann oder ob es im Internet eine Seite gibt, die das automatisch macht?

Hallo Mathe-Experten,

an folgender Aufgabe (Ableitung einer natürlichen Logarithmus

funktion) bin ich gerade am verzweifeln.

Trotz meiner Meinung nach korrekter Anwendung der Kettenregel erhalte ich ein falsches Ergebnis.

So: Bilder sagen mehr als 1000 Worte!

Danke und Gruß carbonpilot01

Verstehe es irgendwie nicht ganz... könnte mir ein schlauer Kopf erklären, wie ich das herausfinde? Bzw. was überhaupt eine Zweierpotenz ist? :)

Ist ein Hauptraum in der linearen Algebra das gleiche wie der von den Eigenvektoren aufgespannte Vektorraum?

Soweit ich weiß ist eine Folge eine spezielle Funktion mit der Definitionsmenge der natürlichen Zahlen, der Graph besteht also aus Punkten.

Soweit ich dass jetzt verstanden habe werden bei einer Reihe alle Folgenglieder aufaddiert * , also wäre eine Reihe ja letztlich nur eine einzige Zahl.

also: Glied 1 einer Folge + (Glied1+Glied2) + (Glied1+Glied2+Glied3)...

Stimmt das?

Hallo

Ich möchte den Grenzwert im Positiven gegen unendlich für die Funktion

ln((x+1)/(x-1))/(1/x)

ermitteln

Also Lim x gegen unedlich

Ich verstehe leider nicht wie ich rechnerisch, bei der Grenzwertbestimmung, vorgehen muss.

..eurer Meinung nach?

was bedeutet das? siehe bild

Ich weiß grade nicht wie ich dies Berechnen soll, einfach normal nach gauß umformen und a wie eine normale variable behandeln? Es handelt sich um Aufgabe 1

Die Aufgabe:

Peter wird in 3 Jahren dreimal so alt sein, wie er vor 5 Jahren war. Wie alt ist Peter?

Meine Rechnung: Also der Peter in 3 Jahren heißt Peter + 3

"......dreimal so alt sein, wie er vor 5 Jahren war."

Der Peter war also vor 5 Jahren : Peter - 5

und das dreimal so viel: 3(Peter-5)

DIe Gleichung lautet also:

P + 3 = 3(P - 5) (Peter in 3 Jahren gleich Peter vor 5 Jahren)

Bei mir kommt als Ergebnis: P=4

Richtiges Ergebnis ist aber: P = 9

Mein Rechenweg ist also falsch, aber ich hab doch alles logisch aufgestellt? Bitte um ausführliche Hilfe:(

Hallo Com,

ich beschäftige mich momentan mit dem Handschlaglemma und kann mir die Formel nicht erklären (Bild).
Was bedeutet das kleine v?
Oder noch besser: Kann mir jemand die ganze Formel erklären?
Danke!

Hallo liebe User,

ich habe eine Aufgabe aus dem Internet zur Übung genommen. Es sind Textaufgaben die ich in Gleichungen umwandeln soll.

Ich habe die Aufgabe gerechnet und mit dem anderen Ergebnis vergliechen und meine Lösung ist angeblich falsch. Ich denke aber dass mein Rechenweg richtig ist! Bitte, sagt mir wieso mein Rechenweg falsch sein soll.

Die Aufgabe:

Frau Mertens ist dreimal so alt wie ihr Sohn Lars. In 14 Jahren ist sie nur noch doppelt so alt wie ihr Sohn. Wie alt ist Lars, wie alt seine Mutter

Meine Rechnung:

M = 3L

3L = 2(L + 14)

3L = 2L + 28

L= 28

Angeblich soll aber dies richtig sein:

3x = 2x + 14 → x = 14; 3x = 42 Lars ist 14 Jahre alt, seine Mutter 42.

Warum???? Bitte um Hilfe.

Die aufgabe:

Zwei Personen wollen ein Pferd für 11 Gulden kaufen. A sagt zu B: "Gib mir ein Drittel von deinem Geld, so will ich meines dazutun und das Pferd bezahlen." B sagt zu A: "Gib mir von deinem Geld ein Viertel, so will ich mit meinem zusammen das Pferd bezahlen." Nun frage ich, wieviel Geld jeder gehabt hat.

Mein Rechenweg:

A + B = 11 (Person A und Person B haben insgesamt 11 Gulden, die für den Kauf benötigt werden)

A = 11 - B (Anteil der Gulden von Person A)

A + 1/3B = 11 (Der Anteil von Person A plus den den Anteil von Person B ergeben 11 Gulden)

B + 1/4A = 11 (Jetzt der Anteil von Person B plus den Anteil von Person A ergeben 11 Gulden)

Wie fasse ich das alles zusammen damit es den Sinn ergibt?

Ich habe in eine der Gleichung das A = 11 - B eingesetzt. Und es kommt wieder falsch raus. Dann habe ich das Additionsverfahren verwendet und kommt wieder falsch raus.

Hab viel mal ausprobiert und für X kam bei mir verschiedene ergebnisse raus z.b bei Additionsverfahren kam bei mir x = 9 raus. Beim Einsetzen x=7,5

Bitte um Hilfe:( Eine ausführliche Erklärung würde mir sehr helfen.

Ist sowas möglich?

Hallo Com,

ich beschäftige mich momentan mit der Linearen Algebra, bzw. Vektoren. Nun zeigt in meinem Bild mit dem Pfeil gekennzeichnet, die Gleichungen, die bi definieren.
Was bedeutet das erste Zeichen? Und wer es vielleicht auch weiß, wie rechne ich damit? Dass die Buchstaben zu den Matrix(en?) gehören, kann ich mir denken. Was jedoch sagen diese Gleichungen aus?

Also genau die Frage wie in der Überschrift.

Bild sagt nochmals die Aussage aus. Ist die richtig oder falsch?

Kann man die 2 x 2 Nullmatrix schreiben als " 0 " ?

Kann ich also schreiben:

( (1,1),(1,1) ) - ( (1,1),(1,1) ) = ( (0,0),(0,0) ) = 0

Bei der vertikalen Streckung werden doch alle Faktoren mit dem Faktor multipliezrt. Also wenn die Gleichung y=2(x-3)^2+5 lauten würde und man das vertikal mit dem Faktor 3 strecken würde, käme doch folgendes raus: y=6(x-3)^2+15

Würde mich sehr um eine Hilfe freuen! Ich weiss eben nicht, wie man e & f herausfindenkann! Danke !

Das ist die Aufgabe, aber meine einzige Frage ist: was sind 6-stellige Zahlen des Zehnersystems?😂

Hallo! Im Matheunterricht haben wir vor kurzem eine Aufgabe behandelt: ,,Du wirfst zwei Würfel gleichzeitig, wie groß ist die Wahrscheinlichkeit für einen Pasch?'' Zuerst wäre ich davon ausgegangen, dass Omega 21 Möglichkeiten enthält, da ich dachte, dass z. B. 1,2 und 2,1 als nur eine Möglichkeit gezählt werden, weil beim gleichzeitigen Würfeln die Reihen folge ja eig. egal ist. Nun hat mein Lehrer gesagt, es sei doch irgendwie möglich die zwei Würfel auseinanderzuhalten und somit hat Omega 36 Möglichkeiten. Aber jetzt kommt meine Frage: wieso steht dann in der Aufgabenstellung ,,gleichzeitig''? Wenn man die Würfel nacheinander Würfeln würde, dann wäre es ja trotzdem das gleiche Experiment, weil da Omega ja die gleichen 36 Möglichkeiten hat. Oder kann mir jemand erklären wo da der Unterschied liegt?

Ich mach grade meine Mathehausaufgaben und versteh Aufgabe 10 nicht ich hab schon mehrere aus meiner Klasse gefragt und die können das auch nicht
Kann mir das einer erklären?
Danke schon mal im Voraus

Damit wäre das mathematische Rätsel gelöst, dass es doch eine kleinste positive Zahl gibt, die mit der kleinsten negativen Zahl aber identisch ist. Und was ist die zweitkleinste Zahl, die drittkleinste ect.?

Hallo,

ich hab ein problem beim umformen dieser gleichung nach R:

(R*L) / (1+C*R^2) = R1

Vielen Dank im Voraus!

Hallo! In Mathe verstehe ich den Unterschied zwischen Vorzeichen (positiv,negativ) und zwischen Operationzeichen (addition,subtraktion) nicht.Für mich sehen sie gleich aus oder verstehe ich was falsch?

H_a (untergestellt) ist 12 cm lang.
Und a ist 18 cm lang.
Meine Lösung für h= 15 cm
Und für s= 23,43 cm.

Danke,

Lg

Ich muss da etwas in Abhängigkeit von a ausrechnen und da kommt bei mir das hier raus:

s = √{(1/2 * √{a² + a²})² + (2a)²}

Diese Klammer {...} soll die Wurzel darstellen, da ich nicht weiß, wie ich das auf dem Computer schreiben soll. Ihr seht hier also eine große Wurzel, in der sich eine weitere Wurzel befindet √{...√{...}...}

Im Ergebnis steht aber folgendes: s = 3/2*√{2a}

Es ist so, dass es schon länger her ist, dass wir das hatten und kommende Woche schreibe ich meine Abschlussprüfungen. Ich bin mir ziemlich, dass wir es nicht exakt genauso wie im Ergebnis darstellen müssen, aber ich bräuchte Hilfe dabei, wie man das etwas genauer zusammenfassen kann.

Wie ist das mit den Wurzeln und dem Quadrat? Wann heben die sich gegenseitig auf (schließlich habe ich ja mehrere Quadrate in der Wurzel)? Was würdet ihr als nächstes tun, um mein Ergebnis näher zusammenzufassen?

Hier ist die Aufgabenstellung:

31.0 Das Quadrat ABCD (Seitenlänge a) ist Grundfläche einer Pyramide mit der Höhe h = 2a, deren Spitze S senkrecht über dem Diagonalenschnittpunkt M des Quadrates ABCD liegt.

(31.1 Zeichen Sie ein Schrägbild der Pyramide für a = 6 cm; ω = 30°; q = 1/2; [AB] liegt auf der Schrägbildachse.)

31.2 Bestimmen Sie die Länge s(a) der Seitenkante sowie den Flächeninhalt S(a) einer Seitenfläche in Abhängigkeit von a.

[Ergebnis: s(a) = 3/2*√{2a}, S(a) = √{17}/4*a²]

Hey Leute!

Also Folgendes:

Wenn ich das Integral aus 1/ln(x) suche, bekomme ich überall nur angezeigt, dass es li(x),j also der Integrallogarithmus ist. Dieser ist ja eine Spezielle Funktion. Meine Frage ist jetzt nur: Wie kommt man auf den? Man muss ja mit irgendwelchen Rechenschritten von dx/ln(x) auf li(x) kommen. Die finde ich aber nirgends!! Oder kann man das Integral nicht anders als durch Approximation bestimmen?

Danke schon mal für Eure Antworten! :) JTR

Liebe Mathematik-Interessierten,

Welches Gebiet hat euch am wenigsten interessiert? Und weshalb?

Wie kommt man von der gleichung auf x^2-55x=-250 ??(Der 5.Teil einer Affenherde minus 3, quadriert, ging in eine Höhle, nur einer war noch zusehen. Wie viele Affen waren es?

Die Aufgabe geht so: Ein Hotel hat insgesamt 78 Zimmer damit insgesamt 119 Betten. Wie viele Einzelzimmer und wie viele Doppelzimmer hat das Hotel? Ich komme da echt nicht weiter.

Also das x mal x x hoch 2 ergibt weiß ich, aber wie ist es z.b. mit 9x mal 2x? Danke im Vorraus.

Warum sind 1kwh 3600000Joules
Wie sieht die rechnung dafür aus

Ich habe folgende Matheaufgabe bekommen (und nein... ich kann meinen Lehrer nicht einfach fragen)

Ich soll 3x(x-2)=3(x²-16) irgendwie umformen, dann in die Quadratische Formel (siehe Foto) packen und so mit die Nullstellen bestimmen.

Ich bin echt ratos. Kann mir jemand helfen?

Hallo zusammen

Wisst ihr wie man diese Aufgabe löst?

Wisst ihr wie man solche Funktionen mit höhren Grad faktorisiert, um die Nullstellen zu berechnen? Ich komme eben auch nicht auf die Nullstelle.

Auf eure Antwort wäre ich dankbar!

Hallo. Ich habe eine theoretische Frage.

Gehen wir davon aus, ich habe eine Objekt im Gravitationsfreien und Luftleeren Raum. Ich messe nun die Position dieses Objektes und erhalte die Koordinaten (X, Y, Z).

0.1 Sekunde später messe ich die Position wieder und erhalte (X1, Y1, Z1).

Noch einmal 0.1 Sekunden später messe ich die Position wieder und erhalte (X2, Y2, Z2).

Ich gehe davon aus, dass das Objekt sein Flugbahn beibehält.

Wie kann ich die Koordinaten des Objektes a Sekunden später berechnen?

Noch einmal zum Verständnis zusammengefasst:

Pos1 = (X, Y, Z); t = 0
Pos2 = (X1, Y1, Z1); t = 0.1
Pos3=(X2, Y2, Z2); t = 0.2
? PosX=(X3,Y3,Z3); t=a

Wie berechne ich PosX wenn a gegeben ist. (Bspw 0.5)

Vielen Dank :)

Wie rechnet man diese gleichung ? kann mir bitte jemand weiterhelfen

Wie finde ich die Funktionsgleichung einer Parabel (algebraisch), wenn ich zwei Nullstellen z.B (-1|0) und (3|0) sowie einen Punkt z.B (4|1) habe?

Hallo, Da ich mich nun seit einiger Zeit damit beschäftige , bin ich zu der Frage gekommen was uns Algebra\Mengenalgebra und die Mengenlehre von Georg Cantor so bringen? Wozu dienen sie uns im Alltag z.B Handys, Schule oder sowas? Danke im Voraus:) Lg Ganesconner

Gegeben ist die Gruppe (Z_30,mal). Wie finde ich die Erzeuger der zyklischen Gruppe (Z_30,+)? Und warum ist diese Gruppe überhaupt zyklisch?

Vielen Dank!

Hey zusammen
Ich habe hier eine Aufgabe, die ich nicht ganz verstehe ( Nr.4 b)). Könnt ihr sie mir vielleicht erklären?
Lg

Hey Leute, wir behandeln bald das Thema Funktionsscharen und Ortskurven in Mathe. Ich lernen gerne vor, um im Unterricht besser mitzukommen. Mir stellt sich gerade nur die Frage, was Funktionsscharen in der Realität sind bzw. darstellen könnten. Danke :)

Egal ob GTR oder CAS. Gibt man die Mitternachtsformel eingesetzt ein, rechnet die zwei Ergebnisse mit einem + und - b aus, so kommen falsche Ergebnisse heraus.

Warum also muss man die Termine im Zähler, der Diskriminante und dem Nenner erst vereinfachen dass es stimmt?

Ein Taschenrechner macht das doch auch oder?

Habe das Problem, dass mein Extrem wert in der 2. Ableitung Null ist. Muss ich dann nochmal per Vorzeichenwechselprobe das ausrechnen. Oder was muss amn tun?

Bestimme die Lösungsmenge...☺ Schreibe bald ne Arbeit...binomische Formeln,Gleichung, Ungleichungen... Wäre nett wenn ihr diese Aufgabe mit Reche weg lösen könntet damit ich mir das nochmal genauer angucken Kann ...

Meine Permutation ist:

(1 2 3 4)

(2 4 1 3)

Das soll eine große Klammer darstellen Ich soll jetzt die Untergruppe von S4 bestimmen, die von dieser Permutation erzeugt wird. Am besten wäre es wenn ihr mir NICHT einfach nur die Antwort sagt, sondern am besten erklärt ihr mir wie ich das selber finde. Ich google schon den ganzen Abend nach einem Weg das zu machen aber die meisten Websites sind einfach zu kompliziert.

Hallo habe die Relationen {(1,1),(1,2),(2,1),(2,2)} Wie soll ich bei den Relation auf Transitivität prüfen, wenn es kein drittes Element gibt.

Transitivität: a=b und b=c -> a=c

ich hab aber nur a und b ._.

Danke

Bei der mitternachtsformel. Wenn ein minus vor der x hoch 2 ist was macht man dann danke schonmal im vor raus👍

Ich hätte eine Frage um mir selbst die Mathematik zu erleichtern. Gibt es irgendwo eine Übersichst über die mathematischen Teilbereiche? Ich weiß nur das es Funktionen gibt die Gleichungen sind, und algebraisch darstellbar sind; über die Mengenlehre, sprich Gewichte und Rechnen mit irrationalen, rationalen und ja.. das ist bei weitem noch nicht alles.. mir geht es drum, dass mein Hirn mehr Logik damit verbinden kann und es einordnen kann dadurch.. wäre schön wenn jemand was kennen würde :)

Servus, Mein Lehrer meinte heute, dass nur der Graph von y=x^2 Parabel genannt wird. Vor einem Jahr lernte ich jedoch bei einem anderen Lehrer das jeder Graph einer Potenzfunktion als Parabel bezeichnet wird. Was stimmt nun? Falls es stimmt und nur der Graph von y=x^2 Parabel gennant wird, wie werden dann die Graphen der anderen Potenzfunktionen, wie y=x^3 , oder y=x^4 genannt? Vielen Dank schonmal im Vorraus

habe das in einer Lösung von meiner Uni und verstehe grade nur Bahnhof... wäre cool wenn mir das auch wer erklären würde, bin nun sehr verwirrt...

dankeschön

gilt das auch rekursiv? also wenn der Kern nicht= 0 dann nicht bijektiv? und wenn man mit der Determinante Argumentiert, was ist dann stärtker? z.B. wenn man ein A in eine Matrix hinzufügen will muss und wenn man die Determinante ausrechnet also Det=0 die Variable 0 sein muss und wenn man den Kern bestimmt A=2 ist... 2ungleich0... und das wundert mich oder könnten beide Wege gehen? weil in der Lösung steht bei der Uni 0 mit Det aber auch das Kernverfahren gilt ja und das irritiert mich...

(nicht verrechnet 3 Leute gegengucken lassen habe ich)

hi, würde auch gerne Beispiele sehen, weil grade bin ich etwas verwirrt durch ein Uniblatt... nun ist alles bei diesem Thema durcheinander.... danke schon mal im Voraus!

Hallo zusammen

Ich hänge gerade an einer Aufgabe fest, in welcher ich die Eigenbasis einer Matrix bestimmen muss. Nun ist mir nicht genau klar wie ich das mache. Auch die Musterlösung hilft mit nicht sonderlich weiter. Die Eigenwerte habe ich bestimmt: 1.) 1, 2.) -1, 3.) 0 ebenfalls die dazugehörigen Eigenvektoren: Ev1:) (1,0,0)^T Ev2.) (-1,0-1)^T und Ev3.) (0,1,0)^T

Wie gehe ich nun genau vor nach diesen Schritten um die Eigenbasis zu finden?

In der Musterlösung steht nun: span{(-1,0,1)^T} was ich nicht ganz verstehe, da ja ein Vektor nicht reicht um eine Basis zu bilden, oder?

Danke im Vorraus:)

Ich versteh das nicht. Wurde mir schon erklärt aba mir werden immer irgendwelche begriffe auf den Kopf geworfen und ich kapier nix. Würde mich freuen wenn das jemand mal für kleine dummköpfe erklären kann :)

Hallo kann mir mal einer auf die Sprünge helfen warum im 2ten Schritt die 64 von 1/64 beim Umformen dennoch auf der rechten seite bleibt. Kürzt sich diese 64 nicht normalerweise direkt weg ?

Danke schonmal ^^

Wenn ich ein LGS mit 3 Unbekannten und 3 Gleichungen habe und jede der drei Gleichungen 0 ergibt, bekomme ich mit dem Gaußverfahren jedes Mal nur 0 für jede Unbekannte raus, da egal welche Operation ich durchführe auf der rrechten Seite des Systems die Nullen ja nicht weg bekomme :o Wie gehe ich vor?

Danke und mfG

Lukas

Hallo :)
Ich habe hier eine Aufgabe, bei der ich nur b.) lösen konnte, obwohl ich mir auch bei der nicht sicher bin, ob ichs wirklich richtig gerechnet habe.
Jedenfalls hab ich keine Ahnung wie a.) funktioniert und wie man das überprüfen kann.
Ich hoffe, dass mir dabei jemand helfen kann.
Dankeschön! :-)

Hi, also da ich morgen eine Prüfung schreibe wollte ich folgendes fragen : Wie lauten die Formeln der V-Figur und der X-Figur und wann benutzt man sie ? Danke

Hallo,

wir haben zur zeit in mathe lineare Gleichungssysteme und zb beim gleichsetzungsvefahren muss man ja die gleichung zuerst umstellen. und nun wollte ich mal fragen ob mir vllt jmd erkären kann wie das geht zum beispiel an der gleichung 3x+2y=14 und diese nach x UND y umstellen. oder vllt kann mir jemand allgemein erklären wie man das macht. Vielen Dank LG Michelle💕

Hey:) Brauche Hilfe...

Wie kann ich in Texten das ggT und kgV unterscheiden und ausrechnen?

Ich Frage mich gerade wie man einen negativen Exponenten und einen Bruch im exponenten umschreiben kann um nur positive volle Zahlen im Exponenten zu haben: x^-5/6 wäre dann 1 durch die 6. wurzel von x hoch 5 meiner vermutung nach..

Hallo Leute :)
Kann mir jemand helfen ... Hab bald Prüfung und verstehe nicht wie man das Bild und Urbild bildet :/
Ich hab eine Foto angehängt ... Wäre sehr lieb wenn ihr mir dass Beispiel 4.3.13 erklären könntet :)
Bei zweiten Foto sieht man meine Rechnung bei der de Ergebnisse allerdings nicht stimmen
Lg

Ich habe einen R^3 Vektorraum mit 3 Vektoren die die Basis bilden.

Jetzt muss ich einen weiteren Vektor suchen, um auf die Dimension R^4 zu kommen. Der muss ja logischerweise also linear unabhängig sein von den anderen 3 Vektoren.

Das Problem:

Ich habe mal den Vektor v4=(1,0,0,0) genommen und auf lineare Unabhängigkeit überprüft (mit Hilfe eines Gleichungssystems). Ich habe allerdings zu jedem Koeffizient eine eindeutige Lösung gefunden, um v4 abbilden zu können. Setze ich meine Lösung jetzt ein, kommt allerdings nicht v4 raus sondern etwas anderes.

Mein Gleichungssystem ist aber ganz sicher korrekt gelöst worden.

Was bedeutet das jetzt oder gibt es eine andere Möglichkeit um einen linearen Unabhängigen Vektor zu finden?

Kann mir jemand bei diesen Zahlenreihen helfen den Term herauszufinden?

37 53 69 85 und 41 55 69 83 ich weiß, es sind keine schweren Rechnungen aber ich habe im Moment gerade ein grosses Black out -.- Vielen dank für alle Hilfen (:

Hallo,

ich bin's man wieder mit einem Verständnisproblem bezüglich der Mathematik, genauer der Mengenlehre.

Und zwar geht es um das Vereinigungsaxiom nach ZF. Eigentlich dachte ich, dass ich es verstanden hätte aber dann kam das heutige Übungsblatt.

Hier einmal der Kontext:

Wir definieren: M := {0,{0}} (Die 0 steht für die leere Menge)

Jetzt soll ich zeigen ob für alle x aus M gilt: Die Vereinigung von x ist Element von M.

Mein Problem ist jetzt, da ein Element von M ja die leere Menge ist. Ich weiß das nach ZF jedes Element einer Menge selbst eine Menge ist, aber wie kann ich mir logisch die Vereinigung der leeren Menge vorstellen?

Die Vereinigung der leeren Menge würde ja bedeuten es gibt eine Menge A aus der leeren Menge, usw...

Aber das ist doch schon ziemlich widersprüchlich, da die leere Menge keine Elemente/Mengen enthält. Ist also Die Vereinigung der leeren Menge wieder die leere Menge?

Im Anhang befindet sich (hoffentlich) die Angabe um es besser verstehen zu können.

Hoffentlich könnt ihr mir weiterhelfen.

LG,

ZyrranM

Hallo,

ich sitze gerade an einer Matheaufgabe. Sie lautet: Zeigen Sie, dass eine 2x2 Matrix für welche die Determinante ungleich 0 ist, invertierbar sein muss. Nun ist mir ja klar das das Inverse zu einer Matrix A mit 1/Det(A)A auszurechnen ist. So ist der Beweis recht offensichtlich, aber ich frage mich ob es irgendwo einen Beweis für die Aussage A^(-1) = 1/Det(A)A gibt? In Worten: Das Inverse einer Matrix A ist das gleiche wie das Produkt von A und dem Inversen der Determinante von A.

Ich hoffe ihr könnt mir weiterhelfen!

Hi, also ich meine das so, dass wir nicht mit geodreieck und so irgendetwas verschieben müssen, sondern halt irgendwie schriftlich. Also das hier ist mal die Aufgabenstellung. (Also nicht das Ergebnis sagen, das ist nur damit ihr wisst, was ich machen muss:

Der Punkt P(8/-3) wird durch Parallelverschiebung mit dem Vektor v = (-3/4) auf den Punkt P'(x'/y') abgebildet. Welche Koordinaten hat der Punkt P'?

(Über dem v ist noch ein Pfeil und eigentlich stehen -3 und 4 aufeinander, aber ich denke das dürfte klar sein)

Also was muss ich jetzt machen? Muss ich jetzt 8 durch -3 und -3 durch 4 rechnen? Könnt ihr mir bitte ein Beispiel vorrechnen?

Ich habe schon im Interent danach gesucht, aber da wird nur gezeigt wie man das mit einer Zeichnung macht, mit Geodreieck und so aber nicht so schriftlich.

Ich wäre wirklich sehr dankbar für eine Antwort, weil ich das morgen brauche =)

Sollte man beides können oder reicht es wenn man nur eine kann?

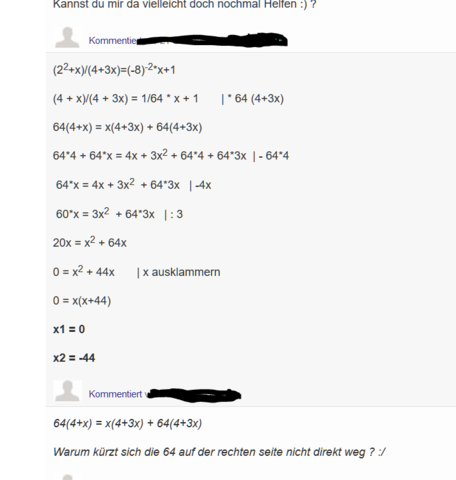
Hi

Stimmen meine Lösungen zu den folgenden Aufgaben:

Aufgaben;

Aufgabe 1

Betrachten Sie das folgende NIM-Spiel: Auf einem Haufen liegen 8 Streichhölzchen. Ein Zug besteht darin, entweder 1, 3 oder 4 Hölzchen zu entfernen. A beginnt, und verloren hat, wer nicht mehr ziehen kann.

a) Für welchen Spieler gibt es welche Gewinnstrategie?

Aufgabe 2

„Schokoladenspiel“: Zwei Spieler A und B sitzen vor einer Tafel Schokolade mit m Zeilen und Spalten und ziehen abwechselnd, beginnend bei A ( n m n, ∈` ). Das Täfelchen oben links ist irgendwie markiert. Ein Zug besteht aus dem Wegbrechen (und Essen) eines Teils der Schokolade entlang irgendeiner Kante (einige Zeilen oder aber einige Spalten). Dabei darf das markierte Täfelchen oben links nie entfernt werden. Verlierer ist, wer am Ende nur noch das markierte Täfelchen oben links vor sich sieht und folglich nicht mehr ziehen kann. Spielen Sie das Spiel mit der folgenden Schokolade. Bild 1 angehängt.

a) Analysieren Sie das Spiel im Hinblick auf Gewinnstrategien . (Ist damit gemeint das man zeigen soll ob das Spiel eine Gewinnstrategie hat, oder ob man zeigen soll welcher Spieler eine Gewinnstrategie hat?)

Aufgabe 3:¨

Wir verallgemeinern das Spiel aus Aufgabe 2: Zwei Spieler A und B sitzen vor Streichhölzchen ( ) und ziehen abwechselnd, beginnend mit A. Ein Zug besteht aus dem Entfernen von n n∈` x Hölzchen, wobei 1≤ ≤x a . Dabei ist a eine Konstante, nämlich die maximale Anzahl Hölzchen, die in einem Schritt entfernt werden dürfen. Verlierer ist, wer nicht mehr ziehen kann. Analysieren Sie das Spiel im Hinblick auf Gewinnstrategien.

Meine Lösungen:

Aufgabe 1;

a) Für den Spieler B gibt es eine Gewinnstrategie.

Aufgabe 2:

a) Für den Spieler A gibt es eine Gewinnstrategie

Aufgabe 3:¨

Bild 2 angehängt,

thx

Hallo Zusammen

Ich bin grad bei den schweren Bruchgleichungen dran. Grundsätzlich ist das vorgehen ja folgenderweise bestimmt:

1. Bestimmen des Definitionsbereichs
2. Brüche gleichnamig machen
3. Mit dem Hauptnenner die Gleichung multiplizieren
4. Gleichung lösen
5. Lösungsmenge angeben

Jetzt passiert es aber, dass ich mit diesem vorgehen bsp bei der Nummer 6 völlig drauskomme. Könnt Ihr mir diese Aufgaben schrittweise erklären? Falls möglich bitte an das Schema von oben halten. Ich muss die Sache so angehen, sonst droht eine Verwirrung.

Vielen Dank und die besten Grüsse :-)

Hallo,

bei der Abstandsberechnung Punkt Ebene mit Lotgeraden muss ich wissen ob der Normalenvektor zur Ebene hin oder von der Ebene weg zeigt. Woran erkenne ich das?

Vielen Dank!

Ist 2r das gleiche wie r,,hoch 2 ,, ??? Danke

Hi Leute,

ich verzweifle fast daran folgenden Term nach a umzustellen (kein Hausaufgabe, aus eigenem Interesse):

x = sin(a) + sin(a + b)

Eigentlich sieht die Gleichung so aus:

x = q * sin(a) + w * sin(a + b) + e * sin(a + b + c)

Aber es wäre schon mal ein Fortschritt die obere zu lösen :)

Danke im voraus, Marvin

Hallihallo,

bin grade für meine Mathe-Abiprüfung am lernen und frage mich wann ich eigentlich eine Inverse brauche? Habt ihr vielleicht ein Beispiel? (Am besten direkt als Anwendungsaufgabe? Muss aber nicht sein.)

Lieben Dank im voraus!

Es geht jetzt nicht unbedingt um das Thema, sondern eher allgemein.

Ich schreibe bald eine Prüfung in Linearer Algebra und wir dürfen uns für die Klausur eine 4 Seiten, handschriftlich geschriebene, Formelsammlung machen. Laut dem Prof. darf da alles drauf, Zahlenbeispiele etc. etc.

Ich weiß nicht, ich könnte da jetzt einfach das wichtigste drauf klatschen, aber hat jemand einen Tipp, ein Beispiel vllt. o.ä. wie ich das am besten machen kann, damit ich bei der Prüfung nicht stundenlang eine Sache suche?

Hallo,

ich studiere Mathematik und bin momentan frisch im ersten Semester und würde gerne wissen wie ich das Thema der Linearen Algebra am einfachsten verstehen und lernen kann? Mir fällt es etwas schwer, da ich in der Oberstufe nicht angemessen in dem Bereich unterrichtet wurde(ist aber eine andere Geschichte). Naja und in der Uni wird alles so - meines Erachtens - schwer und wissenschaftlich erklärt, dass ich meist den Überblick verliere und kaum mitkomme oder etwas verstehe. Ich mache mir auch große Sorgen wegen der Prüfung später, dass ich sie vielleicht nicht bestehe und ich möchte es so gerne lernen und habe auch die Motivation dazu. Die Bücher in der Bibliothek sind auch - ich sage mal - gefühllos in ihrer Interpretierung. Vielleicht hat ja jemand von euch mal Erfahrung gehabt im Studium oder teilt das selbe wie ich und könnte mir dabei etwas behilflich sein und Ratschläge teilen?

MfG

Guten Tag

Darf man den Nenner und den Zähler "umdrehen"?

Hier ein Beispiel

15:x = 1500:6

Darf man dies nun so umdrehen so das

x:15 = 6:1500

Hallo :)

Und zwar war ich ne Woche krank wegen einer Op und in der Zeit wurde ein Thema behandelt welches ich mir selbst nicht wirklich erschließen kann und zwar das Faktorisieren. Einfache Gleichungen sind kein Problem. Substitution kann ich auch nur die quadratische Ergänzung und das Zerlegen von Polynomen der Form p(x)=x^6-1 fällt mir noch schwer.

Ich würde mich freuen wenn mir jemand erklärt wie man Polynome der Form (a^n +- b^n) in die einzelnen Faktore zerlegt. Am besten am oben genannten Beispiel (p(x)=x^6-1). Das Ergebnis ist p(x) = (x + 1)·(x - 1)·(x^2 + x + 1)·(x^2 - x + 1) bevor es wieder heißt Hausaufgaben fragen etc. (Die Lösung ist aus dem Untericht jedoch hab ich es nicht verstanden und der Lehrer meinte ich solle es mir selbst beibringen da ich ja krank war :/).

Die Formel die wir bekommen haben ist: p(x) = (a^n - b^n) = (a-b) (a^n-1 - a^n-1 * b-ab^n-1 - ... - b^n+1)

Wie ich die anwenden soll weiß ich nicht...

Hoffe das mir hier jemand hilft und vllt. mir Tipps geben kann wie ich mich darin verbessern kann. Also wo es Übungen gibt etc.

LG

PS. "^" steht für "hoch"

Ich komme bei einer Mathe Aufgabe nicht weiter. Ich soll das hier in Faktoren zerlegen: 144x² - 25z² + 24x + 1 Also man muss doch sicher mehrfach ausklammern, aber wie funktioniert das? Könnte es mir jemand allgemein erklären? Und dann auch noch am Beispiel?

Hallo, ich wurde im 10. Semester meines Ingenieur-Studiums (Bachelor) exmatrikuliert und habe nun keine Chance das Master-Studium anzufangen. Alles scheiterte an Algebra, was ich ein paar Mal geschoben habe und dann 3 Mal vermasselt habe (Durchfallquote: 60-70 %). Die meisten haben es nach drei Versuchen doch noch geschafft oder schon im 3. Semester exmatrikuliert worden. Ich fühle mich so schlecht, weil es immer mein Wunsch war das Ingenieur-Masterstudium zu beginnen. Was kann ich tun? Mir fehlt nur noch die Bachelorarbeit und dieser eine Schein. Mein Notendurchschnitt ist 2,4 (also recht gut).

Morgen,

ist das richtig? ∞/∞=1

Und was ist wenn ich ∞/1 habe oder 0/∞ ?

Danke schon mal :)

Hi ich muss ich GFS über WUrzelgleichungen schreiben allerdings konnte ich im inet nichts finden was erlaubt das man Wurzelgleichungen mit der Mitternachtsformel (ABC-Formel) aufzulösen.

Ich frage das ganz allgemein: Ist es sinnvoll, bei Mathe zu versuchen, die Formeln wirklich zu verstehen oder sollte man lieber akzeptieren, wie sie sind und stumpf auswendig lernen wie in der Schule ? Ich finde es nämlich sehr schade, dass Formeln in der Schule nicht wirklich erklärt werden..........

Hallo zusammen

sitz hier grad an meinen Übungsaufgaben und komm irgendwie nicht klar. Müssen hier zur bestimmung der Eigenvektoren den span des ker(A) berechnen.

ker(A) = ker(A - lambda * I_n) also I _n soll die Einheitsmatrix sein..

soweit so gut.. bsp: A = ( 1 1 0 / 1 0 1 / 0 1 1 ) lambda = 1

dann komm ich auf ker ( 0 1 0 / 1 -1 1 / 0 1 0 )

was der Kern jetzt genau ist, weiß ich auch nicht so genau.. also falls das dabei beantwortet werden könnte, wäre das auch ganz nett :D aber primär interessiert mich erstmal: wie bilde ich denn nun aus diesem kern den span? und was ist der span überhaupt mal ganz plump ohne große mathematische Formulierungen zu verwenden?

Besten Dank für kommende antworten!

Hi, ich habe zwei Logarithmusfunktionen und soll jetzt den schnittpunkt berechnen ich habe soweit alles umgestellt aber jetzt komme ich nicht mehr weiter… :/ Bitte um einen Tipp damit ich weiter komme :) vielen dank schon mal im vorraus (Aufgabe als Bild im Anhang ;)

Ich hätte eine Frage zur unten angegebenen Schreibweise einer Hyperebene (außerdem gilt: V ist Vektorraum, 0 ≠ c ∈ V, α ∈ IR).

In einer Aufgabe sollte im IR³ geprüft werden, ob es einen Schnittpunkt zwischen einer Gerade und einer bestimmten Hyperebene gibt. Dazu wurde das Skalarprodukt aus dem Richtungsvektor der Gerade und dem Vektor c der Hyperebene aus der unteren Schreibweise gebildet. Dieses war 0, somit mussten Hyperebene und Gerade parallel sein und es konnte keinen Schnittpunkt geben.

Bedeutet dies, dass c im Dreidimensionalen quasi der Normalvektor ist, der senkrecht auf der Ebene steht bzw. (auch in anderen Dimensionen) angibt, in welche Richtung/Dimension die Hyperebene nicht "vorstößt"?

(P.S.: Hausaufgabe? Haha... Diese Aufgabe ist meilenweit über dem Schulstoff. Also unterstellt mir nicht nochmal so einen Unfug. Außerdem habe ich die Aufgabe bereits gelöst und mir geht es um das korrekte Verständnis. Somit sollte ich hier durchaus richtig sein!)

Hallo

Ich habe hier eine Frage zum Texas Instruments 30 ECO RS:

Warum muss man bei diesem Taschenrechner zum errechnen des gesuchten Exponenten (log des Numerus) / (log des Basis) rechnen? Begründung/Beweis?

Gibt es eine Funktion im Taschenrechner welche das eintippen von log Basen erlaubt?

Danke

Ich hab ein Problem wegen Mathe. Kann der normalenvektor einer ebene als dritte Koordinate eine 0 haben? Also zb (4/-2/0) halt als Vektor untereinander geschrieben? Bitte schnell Antworten, danke!!