Noch 2 Wochen bis zur "Pflanzen und Pilze"-Klausur und das Bobbes geht ordentlich auf Grundeis. Nicht zuletzt weil davor noch 2 weitere Klausuren anstehen (eine davon sogar 20 Stunden vor Pflanzen & Pilze), so daß bereits jetzt "im Voraus gelernt" werden muß. So auch mit folgender Aufgabe:
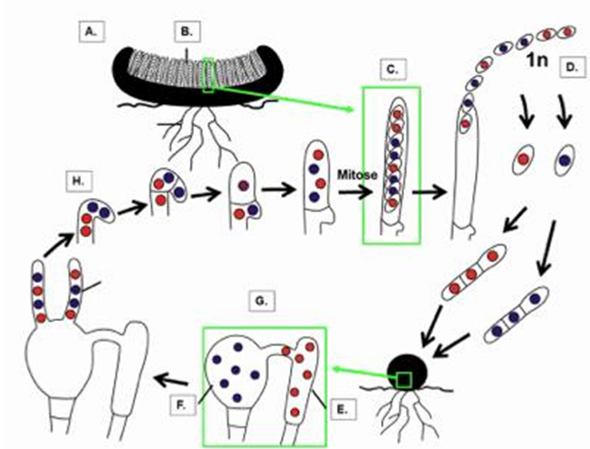
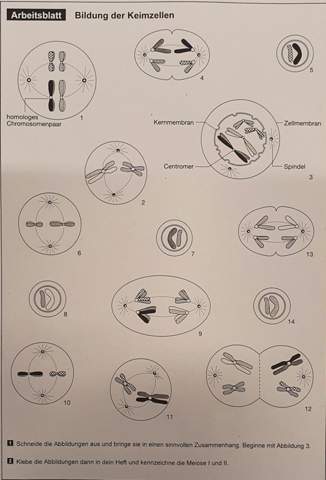
Beschriften SIe diesen Entwicklungsang einer Ascomycota mit den entsprechenden Fachbegriffen, die sie hinter die Buchstaben schreiben. Schreiben Sie zudem die verschiedenen Zuständ und Ereignisse des KErnphasenwechselns an die richtigen Stellen. Benutzten Sie dabei die bekannten Abküprzungen (1n, 2n, n+n, K!, P!, R!)
A hätte ich jetzt gesagt: Apothecium. Ich bin nur nicht sicher, ob "n+n" oder "2n".
B: Hymenium (1n)
C: Ascus. Auch hier bin ich nicht sicher ob 2n oder 1n, weil ja davor schon die Mitose stattgefunden hat.
D: Ascosporen 1n
E: Antheridum 1n
F: Ascogonium 1n P! Hier findet die Plasmogamie statt
G: Gametogamie: n+n
H: Haken K! Hier findet Karyoamie statt.Wäre dann auch wieder n+n. Oder soll man dann schon scheiben 2n, weil ja dann die Zellkerne miteinander verschmelzen.
Ich bin mir auch nicht sicher, wo genau man "R!", also Reifeteilung hinschreiben soll. WIr haben ja eine Meiose, wenn die Ascus-Mutterzelle (oben links im Bild, 2 Schritte vor "C") aus einer diplodien Zelle 2 haplodie Zellen macht und dann nochmal die Mitose wenn die 4 haploide Zellen verdoppelt werden. Aber wo genau packt man jetzt das "R!" hin, um die Professorin (oder wahrscheinlich deren Wissenshaftliche Mitarbeiter, die die Klausur eher korrigieren) glücklich zu machen? ChatGPT meint, im Schritt A, also im Hymenium, aber ich trau dem Braten nicht.
Mit gestreßten Grüßen,
Jensycota 81ales