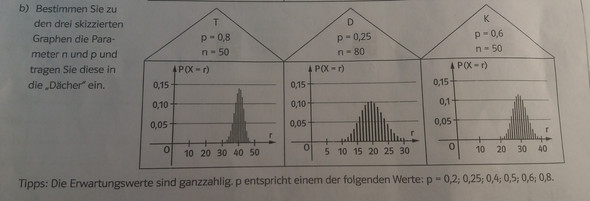
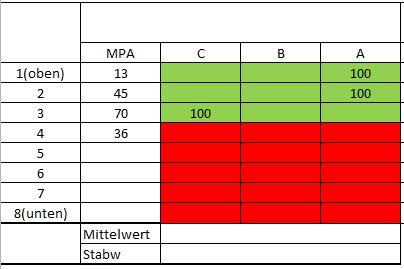
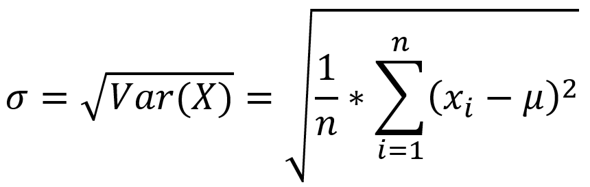Hallo ihr lieben,
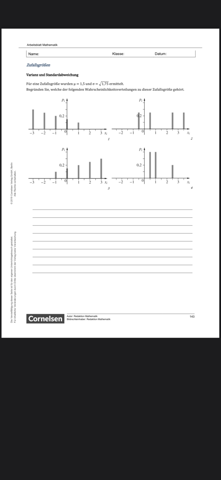
ich habe gerad ein bisschen Probleme bei folgender Aufgabe und hoffe ihr könnt mir weiterhelfen. Die Aufgabe im Wortlaut:
Meine bisherigen Ansätze:
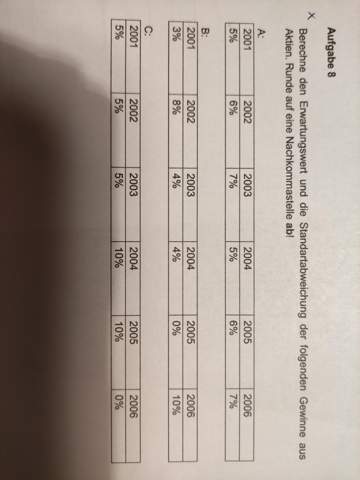
a) i) Erwartungswert E (x) = 1/2 * 10 + 1/6 * 5 + 1/3 * 20 = 12,5
ii) Varianz: (10 - 12,5)² 1/2 + (5 - 12,5)² * 1/6 + (20 - 12,5)² * 1/3 = 31,25
iii) Wurzel von 31,26 = 5,5902
b)
α) Es weden alle Individuen gezogen. Der Ausgang ist deterministisch und damit (richtig oder Quatsch?)
β)Für die Kovarianz habe ich folgende Formel im Internet gefunden
ist die Varianz, also 31,25. Aber was ist der hintere Term, also
γ)Hier hätte ich gesagt 1/30 * 31,25 = 1,0412. Hier bin ich mir nicht sicher, ob es nicht doch zu einfach ist.
c) Auch hier wieder eine Formel durch Internetrecherche
Für n hätt' ich jetzt 30 eingesetzt, da dies die Stichprobengröße ist. Aber was ist p, wenn die Abweichung 2 sein soll? 200 %?
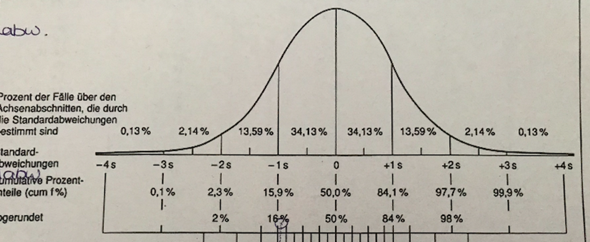
Im Skript ist die Ungleichung von Chebyshev wie folgt definiert:
"Y sei eine reellwertige Zufallsvariable mit endlichem Erwartungswert μ. Dann gilt für alle ε >0: P(|Y−μ|≥ε) ≤ \frac{1}{ε^2}Var[Y] ".
Den Erwartungswert und die Varianz habe ich aus Aufgabenteil a). Aber was wären Mü und Epsilon?
Danke und liebe Grüße