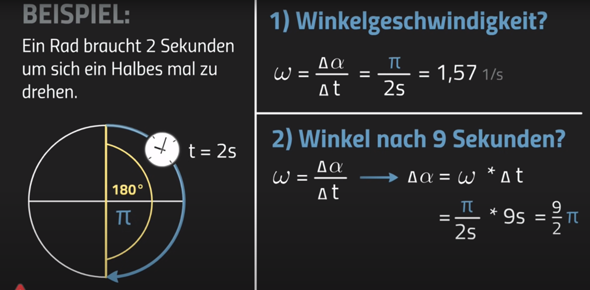
Warum verdoppelt/ halbiert sich die Zentripetalbeschleunigung, wenn sich r halbiert, je nachdem ob man v oder ω betrachtet?
Ein Transporthubschrauber hat einen Rotor eines bestimmten Radiuses.
Argumentiere nun anhand der Formeln ohne Rechnung, wie sich diese ändert, wenn man einen Punkt in der Mitte des Rotorblattes betrachtet.
1) Wenn man die Formel a(zp)=ω^2⋅r benutzt, halbiert sich die Zentripetalbeschleunigung auch, wenn man den Radius halbiert.
2) Wenn man die Formel a(zp)=v^2/r benutzt, verdoppelt sich die Zentripetalbeschleunigung, wenn man den Radius halbiert.
Rein von der Formel her gesehen, ergibt das für mich Sinn. Aber praktisch nicht so sehr...
Wenn man 1) betrachtet: Wenn sich r halbiert, muss der weiter-innere Punkt ja in derselben Zeit den gleichen Winkel hinter sich bringen, wie der äußere Punkt. Ich stell mir das mit dem Abbiegen eines Autos in einem Kreisverkehr vor, da man dann, wenn der Kreis enger ist, das Lenkrad viel weiter umdrehen muss, also die Richtung viel stärker ändern muss, also eine größere Geschwindigkeitsänderung, also eine stärkere Beschleunigung hat...
Aber nein, die Formel sagt, die Beschleunigung wird halbiert...
Wenn man 2) betrachtet: Wenn sich r halbiert, legt der weiter-innere Punkt ja in derselben Zeit eine viel kürzere Strecke zurück als der äußere Punkt, daher müsste v ja viel langsamer sein...
Aber nein, die Formel sagt, die Beschleunigung wird verdoppelt...
Wieso ich verstehe das einfach nicht T.T
Würde mich sehr über jegliche Antwort freuen, LG Mayu